In order to derive proper motions, the x-y-positions
measured on different plates were "reduced" to the
system of an external stellar reference catalogue by means of
a simultaneous adjustment of all plates.
The solution was approached with an iterative
reduction scheme, in which single plate adjustments and
astrometric parameter determinations were alternated until convergence
in the plate constants and in the positions and proper motions of all
objects was reached (iterative overlap algorithm).
Two solutions were tried, one with the PPM catalogue and one with
data from the preliminary catalogue H37
.
Here we describe the second solution, which we regard the more interesting
and preferable one. 34 stars from H37 were available in the field
and served as reference stars. In the initial step of the reduction
only the plates with the largest field size and hence the largest number
of reference stars were used (Schmidt and Bruce plates,
reference stars).
The plate-to-catalogue transformations were made with either gnomonic
(astrograph) or equidistant (Schmidt) projection and with a full 2nd
order polynomial plate model. Terms of 3rd order proved to be
dispensable. With five iteration steps a stable solution was reached.
The x-y-residuals of this solution are between 1.0
and 2.0
(rms per plate), depending on plate quality.
The internal errors of the proper motions are generally at or
below the level of 1mas/a, except for very faint stars or stars with
less than 6 observations.
Table 2: Fictitious proper motions of extragalactic sources
obtained with different methods
The measurements of the extragalactic sources were not included
in the plate adjustment procedure, but were introduced only in the
final step of the reduction. Since the stellar reference frame
to which the solution refers is not a priori an absolute frame,
proper motions were assigned to the galaxies in the same way as
to the stars. However these proper motions are fictitious,
because (apart from measuring errors) they indicate the deviation
of the stellar frame from the extragalactic frame. Thus they
provide the key for transferring the stellar proper motions to
the absolute frame. In Table 2 (click here) we give the individual proper
motion values derived for the three different sources. It is not
surprising that the highest internal proper motion accuracy is
achieved with the center of M81. The results from the fitting
approach are in good agreement with those from cross-correlation
and both methods yield essentially the same internal accuracy
of 1mas/a. In the case of M82e the internal accuracy of the
fictitious proper motions is on the level of 1.5mas/a. This
is mainly due to a lower number of observations. In the right
ascension component the proper motion agrees well with that
of M81n within the formal errors, while in the declination
component the deviation between both results exceeds the formal
error by a factor of 1.5. A similar statement holds for the
proper motions of NGC3077. Here, the declination component
is consistent with the results on M81n, but the right ascension
component deviates at the margin of the combined error bar.
The conclusion is that the formal errors somewhat
overestimate the true random accuracy or that a position-dependent
systematic error remains, which can however not be analysed here.
From the individual fictitious motions the local shift between absolute
frame and stellar frame (zero point correction) was determined
by averaging the two results for M81n and taking a weighted
mean over the three sources with weights according to the formal
errors. The result is 
mas/a.
This correction was subtracted from the results for the stars in
order to obtain absolute proper motions.
From the deviations between the individual ficticious proper motions
and the above given mean we estimate that the absolute system
is determined with an accuracy of about 1mas/a. This is
confirmed by comparison with results from other link fields of
the Bonn programme (see Sect. 4.4).
Table 3: Comparison of our (absolute) proper motions
with proper motions from other catalogues
For 95% of the stars the reduction procedure gave proper
motions with formal errors below 1.5mas/a. The formal errors
are distributed around a median of 0.6mas/a in each coordinate.
The external accuracy may be somewhat lower, but at the moment
this can hardly be examined because there are (except from Hipparcos)
no other measurements on our sample of stars with a similar level
of accuracy. Nevertheless, it is worthwhile to compare our results to
other proper motion catalogues. This is done in Table 3 (click here).
For a test of the absolute proper motion zero point the best
catalogue to compare with is that of the Lick Northern Proper Motion
program (NPM, Klemola et al. 1993a,b). A comparison of 12 stars in
common with the NPM yields very satisfactory agreement between the
two extragalactically calibrated systems. Also, the dispersions
in the proper motion differences to NPM fit well to the expected
random error of NPM proper motions of 5mas/a. Dispersions of similar
size are found when comparing to 49 stars from the PPM catalogue.
They slightly exceed the nominal error of 4.3mas/a quoted in the PPM.
The mean differences relative to PPM are marginally
significant, but stay below 2mas/a. Both the mean and the dispersion
of the proper motion differences decrease when the comparison is
confined to stars of the PPM High Precision Subset (HPS).
We conclude that in the field under
consideration the PPM deviates from an absolute system by less
than 1.5mas/a. Totally different results are obtained in
comparison to 31 stars from the ACRS (Corbin & Urban 1991).
There we find mean proper motion differences of +5.2mas/a and
-2.7mas/a and dispersions which are clearly above the nominal
ACRS random error of 4.7mas/a. Hence a local disturbance in the
proper motions of the ACRS must be assumed.
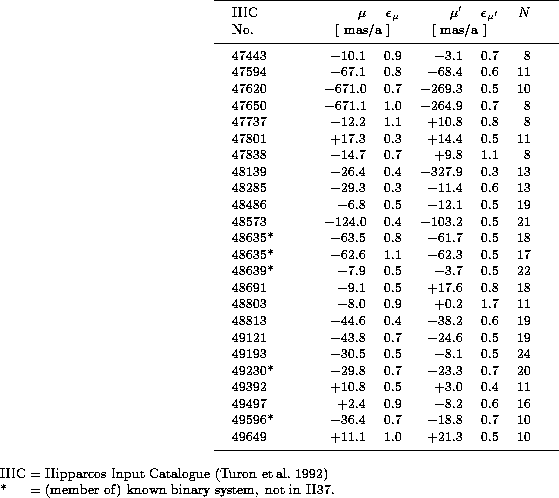
Table 4: Photographically determined absolute proper motions
of Hipparcos stars
Special attention needs to be given to the Hipparcos stars.
Table 4 (click here) presents the proper motion results for a subsample
of 24 Hipparcos stars, for which at least 8 photographic
observations from different epochs were available in the
reduction. In most cases the proper motions are based on
11 to 20 photographic measurements. The internal proper motion
accuracy ranges between 0.3 and 1.1mas/a (in one case 1.7mas/a).
Thus the results reach at least the same level of internal
accuracy as the Hipparcos H37 data and on the average go
beyond this level. Although the results of the reduction are
not completely independent from the Hipparcos data (because
H37 was used as reference catalogue) it is interesting to
examine the degree of accordance between the proper motions
from photography and those from H37.
We find that (apart from the offset between absolute and
stellar frame) the proper motion values generally differ by
less than 3mas/a and that the rms of the differences is
about 1.6mas/a. However, one single case (HIC48691)
of striking disparity is noticed, in which the proper motion
differences exceed the above mentioned rms by factors of
2.8 and 4. This case is displayed in Fig. 1 (click here).
The discordance may be explained by the fact, that
the photographic measurements record the long-term motion whereas
Hipparcos gives the instantaneous motion (during a mission of 3.5
years). Both can be different if the object is an unresolved
binary and its photocenter is affected by orbital motion.
The occurence of this kind of cosmic error in the proper motions
of Hipparcos has recently been discussed by Wielen (1995) and
by Brosche et al. (1995). According to Bernstein (1996, private
communication) HIC48691 yields a significantly increased 
in the Hipparcos data reduction, which suggests that it is
indeed not a single star. In order to confirm the hypothesis of
orbital motion, it would be desirable to have further evidence of
the binarity, for instance from speckle interferometry.
Five stars from Table 4 (click here) (marked by an asterisk) are known as
members of binary systems and were therefore not contained
in the provisional catalogue H37.
Hence they were not used here as reference stars. At a later stage
they may provide an additional check between the photographic
measurements and Hipparcos. However, care has to be taken when
comparing the results because three of these systems are not
photographically resolved.
Owing to the strong global rigidity of the
Hipparcos system, our absolute proper motions can be linked
to absolute proper motions obtained for Hipparcos stars
in other fields of the sky and can be combined with them
into one mean absolute system. This was done with stars from
12 different link fields of the Bonn programme (see
Tucholke 
1996). The residuals from the resulting
mean system give evidence of the reliability of our absolute
proper motion zero point. The local absolute system determined
from the galaxies M81, M82 and NGC3077 agrees with the mean
system of all link fields to within -0.9 and +0.2mas/a,
confirming the estimate given in Sect. 4.2.
Figure 1: Disparity in the results on HIC48691. The points give
photographically measured positions, the open circle marks the mean
position from Hipparcos. The dashed line shows the mean motion
according to the points, whereas the dotted line shows an
extrapolation with the proper motion measured by Hipparcos
Table 5: Photographic measurements of double stars and common
proper motion pairs
We identified in the sample of target stars six visual binaries
and two common proper motion pairs. Our data for these systems
are shown in Table 5 (click here). The visual pairs were selected according to
the proximity of their components.
The proper motion pairs were identified by the fact that the
components show parallel motion
(
10%)
at an angular distance of ordinary neighbours in the field.
While two of the pairs are well-known, the others (with anonymous
component B in Table 5 (click here)) have so far not been mentioned in double
star catalogues.
The physical nature of the pairs was tested by means
of proper motions and photometry. Assuming main sequence stars,
we used the photometry to derive estimates for the distance of the
components and also for their mass. The proper motion difference
was transformed into a relative tangential space velocity and this
was compared to an estimate of the orbital velocity
(cf. Brosche et al. 1992). The result of this test is that Nos. 2,
3 and 5 are very likely physical binaries whereas Nos. 4, 6 and 7
should be optical pairs. However, with No. 7 there is some doubt wether
this is not a physical pair as well. In the case of No. 1 the physical
nature is known directly from trigonometric parallax measurements.
No. 8 is a very interesting case, because the components seem to be
at the same distance of about 60pc, but as a pair they would have
an extreme separation of 40500AU (cf. Odenkirchen & Brosche 1996).
For a more decisive statement about the nature of this pair radial
velocities are needed.
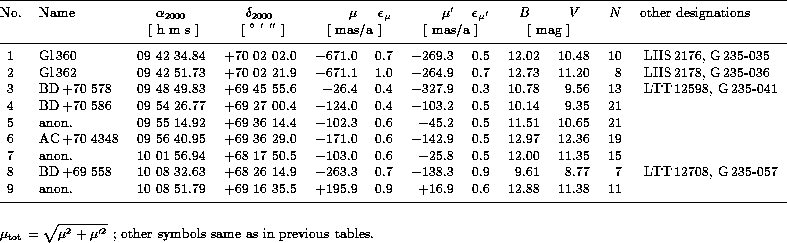
Table 6: Photographic measurements of high proper motion stars
(
100mas/a)
For the majority of stars in our sample (
85%) the total
proper motion is below 50mas/a. About 60% of the stars have
mas/a. In this sense we regard objects with
mas/a as high proper motion stars (HPM).
Nine such exceptional cases were found and are listed in Table 6 (click here).
Five of them occur in the HPM surveys of Luyten (1961, 1976, 1979)
and Giclas et al. (1971), since their total proper motion is
larger than 200mas/a. The pair Gl360/362 has a total proper
motion as large as 725mas/a. This is mostly due to the small distance
of only 12pc (trig.parallax = 0085), from which a
tangential space velocity of 40kms
follows.
By means of our two color photometry some conclusions about
distance and tangential velocity can be drawn also for the other
HPM stars of Table 6 (click here). Taking into account as far as available also
spectral type or trigonometric parallax measurements we derived
for Nos. 4 and 5 tangential space velocities around 45kms
and for Nos. 3 and 8 velocity values of about 65kms
.
For No. 7 we obtained in the same way an estimated distance of
190pc and hence a tangential space velocity of 95kms
.
If our assumptions hold, this object must be attached to the class
of high velocity stars. For No. 9 our photometry yields 
and thereby a distance of only 20pc. However, with a photometric
error of 01 in the color index the distance estimate can rise
to about 35pc. The tangential space velocity would be 19kms
or 33kms
respectively.
In the case of No. 6 the proper motions
reveal that the assumption of an ordinary main sequence star
cannot be true, because it would lead to an unrealistically high
space motion. On the other hand, the assumption that it is a white
dwarf is also not very convincing, because it would place the object
within 5pc from the sun.
Instead we conclude, that this star is most likely a G-type subdwarf.
An estimated absolute luminosity of 
yields a distance of
about 140pc and a tangential space velocity around 145kms
relative
to the sun. This is a typical result for a star belonging to the halo
population.