The detection threshold is depending on the quality of the night,
the star's brightness, the telescope
size and the duration of the observations.
Consequently, for a faint star and/or a poor night this threshold can be
as high as 10mmag whereas for the best cases we find a few
mmags (Fig.1 (click here)).
There can be several reasons why a candidate star yields a null result,
e.g. the internal stellar structure, or atmospheric and instrumental
effects. Also beating of several independent pulsation modes
together with a small time base could simulate constancy.
Nevertheless we consider a star to be constant, if the Fourier spectrum
of the differential light curve does not contain a statistically
significant peak in
the frequency range up to the Nyquist frequency.
Of course, we cannot exclude variability on a lower amplitude level.
For 5 stars (HD31295, HD74873, HD91130, HD125162 and HD179791)
of the presumably constant stars one might be tempted to assume
low amplitude variability. But based on the noise level in the amplitude
spectra of the respective stars, the highest peak is not
statistically significant.
Figure1 (click here) shows the distribution of upper limits for
nonvariability, merging the
results of Strömgren v and b photometry (Table1 (click here)). Models and
observations (Matthews et al. 1996) indicate an amplitude scaling for A-type
stars of
Amplitude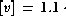
Amplitude[b], justifying our merging procedure.
A typical noise level of 3mmag was achieved for the relevant frequency domain up to
100d
(Fig.1 (click here)). The distribution of the frequencies with the
highest (but statistically insignificant)
amplitudes shows a maximum at 10d
(Fig.2 (click here)), perhaps caused by
insufficiently corrected
sky transparency variations, with no other significant trends.
Figure 1: Distribution of the upper levels for nonvariability for all
observed stars
Figure 2: Distribution of the frequencies for the highest derived amplitudes
After establishing nonvariability among the observed candidate stars
within a given limit, we have investigated their location in a (b-y)
vs.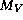 
diagramme. Strömgren colours were taken from Hauck & Mermilliod (1990) and
Handler (1995). No photometric indices are available for HD171948
and HD192424.
The dereddening procedure and calibration in the Strömgren system uses
the results given by Crawford (1979) and comprises
the iteration procedure described by Hilditch et al.
(1983). The reddening for all stars is small (E(b-y) < 0.015), except
for the two cases HD145782 (E(b-y) = 0.03) and HD193281 (E(b-y) = 0.025)
indicating that all stars are within the solar neighbourhood.
Gray (1988) showed that peculiar hydrogen line profiles and
very high 
values, as found in some
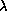Bootis stars, influence 
and hence 
. We have to stress again
that all calibrations are derived for
"normal" type stars. Since the intrinsic error in 
is about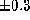 
mag (Crawford 1979), we completely neglect those effects.
Figure3 (click here) shows the location of all observed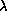 
Bootis stars with the typical
error bars for both parameters
indicated. The variable stars
were taken from Paunzen et al. (1997) and calibrated as just described.
Taking into account the given errors, only 11 "constant" stars lie
within the instability strip (although its hot border is not
unambiguously defined), namely:
HD319, HD74873, HD79025, HD141851,
HD143148, HD154153, HD156954, HD188164,
HD193256, HD193281, HD204041.
On the other hand 12 variable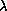 
Bootis stars are placed there,
suggesting that at least 50% of all investigated members inside the
instability strip are
pulsating. If we exclude HD79025, HD154153 and HD188164, since
they are not yet definitely
established members of the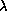 
Bootis group, the ratio increases to 2/3.
This is a remarkable result compared to "normal" type stars in the
same region of the
Hertzsprung-Russell-diagramme. Previous
surveys for pulsating stars in clusters indicate that the incidence of
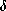Scuti variables is not larger than 35 percent of all stars
within the instability strip (Breger 1975; Slovak 1978).
These results were achieved with limits for nonvariability comparable to
this paper.
On the other hand, we have investigated a biased sample of stars, based
on metallicity.
Nevertheless, since variable and constant members of open clusters generally
have also the
same metallicity,
there is strong evidence that our result is significant compared to
"normal" type stars. The metallicity measured spectroscopically for
chemically peculiar stars very probably is restricted to the surface only, but
the average metallicity for the entire star is "normal".
Figure 3: The location of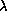 
Bootis stars in a (b-y) vs. 
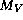diagramme.
The standard line is taken from Crawford (1979), the borders of the instability
strip are from Breger (1979)