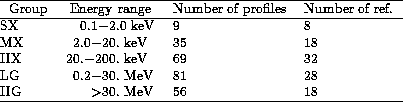
Table 1: Profile groups in the Atlas
In this Sect. we present, as an example of how this database can be used, the results on a few debated problems concerning the changes of the profile structures with energy and time.

Table 1: Profile groups in the Atlas
A relevant point in the study of the P2/P1 ratio is the definition of the phase boundaries of the various features, and particularly that between the Interpeak (or "bridge") region Ip and P2. Different values of this phase, usually in the interval 0.27-0.32, can be found in the literature. We choose the value of 0.3 because the intensity levels at the P1-Ip and the Ip-P2 separations in the soft X-rays are nearly equal. The phase boundaries are: P1(0.95-0.05), Ip(0.05-0.30), P2(0.30-0.47), BKG(0.55-0.85).
The results, obtained using only those profiles with a good enough
statistics, are shown in Figs. 1 (click here)a,b:
the values of P2/P1 (panel a) and of Ip/P1 (panel b) are plotted
as a function
of the effective detection energy, defined as the average of the nominal
photon energy interval (in MeV), weighted with a power law with a photon
index 2.2.
P2/P1 increases from 0.95 at 0.3 keV to ![]() 3.5
at about 1 MeV, while at higher energies it decreases down to values close
to 0.35 in the GeV range. A very similar behaviour is apparent in
the Ip/P1 values, indicating a common origin of these changes.
3.5
at about 1 MeV, while at higher energies it decreases down to values close
to 0.35 in the GeV range. A very similar behaviour is apparent in
the Ip/P1 values, indicating a common origin of these changes.
The increasing trend of P2/P1 for photon energies E< 1 MeV can be described by the simple formula
![]()
Even if it was not derived by means of a best fit,
we think that it could be useful in several cases,
when this dependence must be taken into account:
for example, to compare the time variations P2/P1 at different
energies.
The major problem in the study of the time variations of P2/P1 is that the observations are not well distributed in time and therefore the sampling of the various possible time scales is far from a regular coverage. In the soft-medium X-rays no evidence of significant variations has been found so far: in particular the two GINGA observations (profiles MX 15-1, MX 15-2 and MX 17-1, MX 17-2 in Table 2), 4.5 years apart, give the same P2/P1 and Ip/P1 values. Also the Einstein (SX 05-2) and the ROSAT (SX 07-1) profiles are practically coincident after about 12 years.
Significant variations of the peaks' intensities have been found at
energies higher than 30 MeV. These were discovered in the COS-B data,
which showed a strong decrease of P2, which in September-October 1979
become undetectable (Clear et al. 1987).
Kanbach (1990)
suggested that P2/P1 changes according to a sinusoidal law, with
a period of about 13.5 years, an amplitude of about 0.5
and the maximum epoch at 1972.3.
However, recently Ramanamurthy et al. (1995), after including all the nine
EGRET observations, did not found any firm evidence for
this periodicity, even if variations are evident.
We searched for the sinusoidal behaviour in the hard X
and low energy ![]() rays, where the P2/P1 ratio is higher.
rays, where the P2/P1 ratio is higher.
We analyzed separately the data in the two energy intervals ![]() and
and ![]() : the plots of P2/P1 against time
are given in Figs. 2 (click here)a,b, respectively. No significant periodicity is
apparent: a sine function, with the same phase of the maximum given above,
does not give acceptable fits.
An amplitude of 0.37 is actually found for the highest energy range; however,
using Eq. (1) to scale the measured values to the intermediate energy
of 0.3 MeV (Fig. 2 (click here)c), the much smaller amplitude value
of 0.077 is obtained, suggesting that the previous result can be an artifact
of combining measures at different energies.
: the plots of P2/P1 against time
are given in Figs. 2 (click here)a,b, respectively. No significant periodicity is
apparent: a sine function, with the same phase of the maximum given above,
does not give acceptable fits.
An amplitude of 0.37 is actually found for the highest energy range; however,
using Eq. (1) to scale the measured values to the intermediate energy
of 0.3 MeV (Fig. 2 (click here)c), the much smaller amplitude value
of 0.077 is obtained, suggesting that the previous result can be an artifact
of combining measures at different energies.
Variations of the P2/P1 ratio are nevertheless evident
in the hard X-rays and in the low/high energy ![]() rays.
In particular, in the > 30 MeV range, both COS-B and EGRET detected
significant changes as already said (Clear et al. 1987;
Ramanamurthy et al.
1995). With our choice of the phase boundaries, P2/P1 changes from
0.97
rays.
In particular, in the > 30 MeV range, both COS-B and EGRET detected
significant changes as already said (Clear et al. 1987;
Ramanamurthy et al.
1995). With our choice of the phase boundaries, P2/P1 changes from
0.97![]() 0.20 (HG 13-6) in 1975 to
0.20 (HG 13-6) in 1975 to ![]() (HG 15-3) in 1979 and
from 0.60
(HG 15-3) in 1979 and
from 0.60![]() 0.06 (HG 21-2) to
0.06 (HG 21-2) to ![]() (HG
23-1) in
about one month of 1991.
Both changes are due to an evident decrease of the P2 intensity.
(HG
23-1) in
about one month of 1991.
Both changes are due to an evident decrease of the P2 intensity.
We found significant changes of the P2/P1 ratio at lower
energies.
The values of 1.20 ![]() 0.13 and 1.52
0.13 and 1.52 ![]() 0.08 were found for
the profiles HX 10-1
0.08 were found for
the profiles HX 10-1 ![]() ) in 1976 and HX
) in 1976 and HX ![]() )
in 1981.
An even greater difference is found between the profiles HX 17-3
(
)
in 1981.
An even greater difference is found between the profiles HX 17-3
(![]() ) and HX
) and HX ![]() ): the
former has a P2/P1 ratio
equal to 1.94
): the
former has a P2/P1 ratio
equal to 1.94 ![]() 0.11, while the latter gives 1.535
0.11, while the latter gives 1.535 ![]() 0.025,
In this case, however,
rather than a change in the content of P2, such a difference
should be attributed to a change in P1.
In the low-energy
0.025,
In this case, however,
rather than a change in the content of P2, such a difference
should be attributed to a change in P1.
In the low-energy ![]() -ray profiles no difference more significant
than 1.5 standard deviations has been found.
-ray profiles no difference more significant
than 1.5 standard deviations has been found.

Figure 2: The time dependendece of P2/P1 for the profiles in the
energy range ![]() a) and
a) and ![]() without energy scaling b)
and after the scaling according to Eq. (1) c). The dashed lines
represent the best fit sinusoids
with the same phase of Ramanamurthy
et al. (1995)
without energy scaling b)
and after the scaling according to Eq. (1) c). The dashed lines
represent the best fit sinusoids
with the same phase of Ramanamurthy
et al. (1995)
We used the high statistics ROSAT profile (SX 07-1) as a template for the higher energies and searched for a simple analytical formula able to fit the shape of P1. We choose first a symmetric generalized bell shaped profile
![]()
where ![]() and
and ![]() are the phase and the central phase of the peak,
respectively, and y is the normalized bin content.
are the phase and the central phase of the peak,
respectively, and y is the normalized bin content.
![]() resulted very close to unity and
resulted very close to unity and ![]() to zero, but
the fit was not satisfactory because the shape is not symmetric.
We then modified Eq. (2) introducing different values of b for the
leading and trailing sides and fixing
to zero, but
the fit was not satisfactory because the shape is not symmetric.
We then modified Eq. (2) introducing different values of b for the
leading and trailing sides and fixing ![]() and
and ![]() .
Even if the reduced
.
Even if the reduced ![]() is 1.8 (34 d.o.f.), the result,
shown in Fig. 3 (click here)a, can be considered satisfactory to
achieve a global and simple description of the P1 shape.
The values of the two e-folding constants are
is 1.8 (34 d.o.f.), the result,
shown in Fig. 3 (click here)a, can be considered satisfactory to
achieve a global and simple description of the P1 shape.
The values of the two e-folding constants are ![]() = 0.03 and
= 0.03 and
![]() = 0.022 for the leading and trailing
sides, respectively. The same effect is also apparent at optical
frequencies: the detailed profile of P1
measured with HST shows a trailing side significantly steeper than the leading
one (Percival et al. 1993).
Afterwards, we verified whether the same function is a good description
of the other profiles apart from the normalization.
Significant deviations were found for the profiles in the
hard X and low
= 0.022 for the leading and trailing
sides, respectively. The same effect is also apparent at optical
frequencies: the detailed profile of P1
measured with HST shows a trailing side significantly steeper than the leading
one (Percival et al. 1993).
Afterwards, we verified whether the same function is a good description
of the other profiles apart from the normalization.
Significant deviations were found for the profiles in the
hard X and low ![]() rays. Two examples are shown in Figs. 3 (click here)b and 3c:
one is the profile HX 18-1
rays. Two examples are shown in Figs. 3 (click here)b and 3c:
one is the profile HX 18-1 ![]() ) and the other one is
LG 12-7 at energies greater than 150 keV.
The disagreement is mainly in the trailing side, where significant
excess counts from phase 0.01 onwards are apparent.
At variance, at energies greater than
50 MeV (EGRET 100 bin data reported by
Thompson et al. 1993 - Fig. 3 (click here)d),
there is no evidence for a different shape of the ROSAT one.
) and the other one is
LG 12-7 at energies greater than 150 keV.
The disagreement is mainly in the trailing side, where significant
excess counts from phase 0.01 onwards are apparent.
At variance, at energies greater than
50 MeV (EGRET 100 bin data reported by
Thompson et al. 1993 - Fig. 3 (click here)d),
there is no evidence for a different shape of the ROSAT one.
![]()
Figure 3: The shape of P1 at four different energies:
![]() (SX 07-1) a) used as a template profile to evaluate
parameters of the double exponential function,
(SX 07-1) a) used as a template profile to evaluate
parameters of the double exponential function, ![]() (HX 18-1)
b),
(HX 18-1)
b), ![]() (LG 12-7) c) and
(LG 12-7) c) and ![]() (HG 21-1). Notice that the
analytical shape is not able to represent hard X and low energy
(HG 21-1). Notice that the
analytical shape is not able to represent hard X and low energy ![]() -ray
data, while it is well suited to the high energy
-ray
data, while it is well suited to the high energy ![]() -ray profile
-ray profile
Ramanamurthy (1994) suggested a monotonic decrease with energy of the intra peak separations like for the Vela pulsar. The Atlas permits to search for regular changes over more than six orders of magnitude in energy.
The skewness of P1 is small enough at all energies to estimate
its maximum phase as the centroid of a symmetric distribution.
On the other hand, P2 is fairly symmetric only in
the low energy X and medium-high energy ![]() rays, but it is very skew
in the hard X and low energy
rays, but it is very skew
in the hard X and low energy ![]() rays; the use of a symmetric algorithm
would give a bias toward smaller phase values.
We therefore estimated the phase of the P2 maximum either by computing the
barycentre of a few (typically five) phase bins, for all the energies at which
it can be considered symmetric, or the phase of the bin with the highest content
in the other cases. An uncertainty of half a bin was always taken.
rays; the use of a symmetric algorithm
would give a bias toward smaller phase values.
We therefore estimated the phase of the P2 maximum either by computing the
barycentre of a few (typically five) phase bins, for all the energies at which
it can be considered symmetric, or the phase of the bin with the highest content
in the other cases. An uncertainty of half a bin was always taken.
The phase separation varies between 0.384 ![]() 0.010 and 0.410
0.010 and 0.410 ![]() 0.010,
corresponding to two HG profiles. No significant
evidence for a decreasing trend was found and the data are only slightly
scattered with respect to the mean value 0.399 over the entire (0.1
keV - 100 MeV) interval.
All these peak separations are smaller that
those given by Percival et al. (1993) at optical and UV frequencies, equal to
0.010,
corresponding to two HG profiles. No significant
evidence for a decreasing trend was found and the data are only slightly
scattered with respect to the mean value 0.399 over the entire (0.1
keV - 100 MeV) interval.
All these peak separations are smaller that
those given by Percival et al. (1993) at optical and UV frequencies, equal to
![]() and
and ![]() , respectively.
Elder optical data (Warner et al. 1969;
Cocke & Ferguson
1974) give phase separation values in the interval 0.41 - 0.42, confirming
this difference. We can conclude, therefore, that a decrease of the
P1-P2 phase distance of about 0.015 between the optical and X-ray
frequencies is real, while no significant change is
appreciable at energies greater than about 0.5 keV.
, respectively.
Elder optical data (Warner et al. 1969;
Cocke & Ferguson
1974) give phase separation values in the interval 0.41 - 0.42, confirming
this difference. We can conclude, therefore, that a decrease of the
P1-P2 phase distance of about 0.015 between the optical and X-ray
frequencies is real, while no significant change is
appreciable at energies greater than about 0.5 keV.