2. The mean magnetic field modulus

The determinations of the mean magnetic field modulus presented in this paper rely on the measurement of the wavelength shift between the magnetically split components of the line  , in high-resolution spectra recorded in unpolarized light. The line   has a particularly simple Zeeman pattern, consisting of two components, one component and one component. Each component coincides with one of the components. This pattern, as observed in the star HD 94660, is shown in Fig. 1 (click here), together with those of the neighbouring lines   (a pseudo-quadruplet) and   (a pseudo-triplet). For comparison, we have also plotted the spectrum of the A0p SrCr star HD 133792 (Paper I), which has sharp unresolved lines (the line profiles recorded in this star are mostly identical to the instrumental profile: its projected equatorial velocity must be significantly lower than 3 ).

  
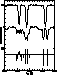
Figure 1: Portion of the spectra of HD 133792 (shifted in intensity by 0.5; unresolved lines) and of HD 94660 containing the lines  ,  , and  , and Zeeman patterns of those lines. The patterns are represented in the conventional manner, by bars whose length is proportional to the relative strength of the components. The components appear above the horizontal (wavelength) axis; the components below it. For the sake of clarity, the wavelengths in the stellar spectra have been reduced to the laboratory reference frame

A Zeeman doublet like   arises from a transition between two levels having a total angular momentum quantum number J=1/2, of which one has a Landé factor equal to zero (that is, this level is unsplit in a magnetic field). In such a doublet, the shift between the wavelengths of the red and blue components is related to the mean magnetic field modulus through the relation:

, where is the nominal wavelength of the transition (in the absence of a magnetic field, that is, for the line under consideration,  Å), and  ÅG. g is the Landé factor of the split level of the transition (g=2.70; Sugar & Corliss 1985). For a Zeeman doublet, Eq. (1) is strictly valid under quite general conditions. The only approximations underlying it are that the populations of the magnetic states pertaining to the same atomic level follow Boltzmann's statistics and that the Doppler effect due to stellar rotation is negligible (see Mathys 1989 for details). The high densities in the photospheres of the Ap stars coupled to the very small energy differences between the magnetic states guarantee the validity of the first assumption. It receives further support from the following empirical argument: significant departures from this approximation would show through as spectral line asymmetries, both in unpolarized light and in circular polarization: such asymmetries are not observed. On the other hand, in a number of the stars studied in this paper, Doppler distortions of the split line components are observed. But this does not question the validity of the second approximation above: more explicitly, the latter states that the rotational Doppler effect is small compared to the magnetic splitting, which is also the condition of magnetic resolution of the lines.

Besides being a Zeeman doublet,   is a particularly good diagnostic line for the determination of the mean magnetic field modulus because

1. it is sufficiently far in the red to take advantage of both the maximum sensitivity of CCD detectors and of the quadratic increase of the Zeeman effect with wavelength (the first magnetic field modulus determinations were performed using photographic plates, that is from the observation of the blue part of the stellar spectra);
2. it is observed in almost all Ap stars (like many lines);
3. the distribution of iron over the surface of Ap stars is usually rather homogeneous, so that the use of a line for magnetic field diagnosis allows a fairly uniform sampling of the stellar surface;
4. among the red lines,   is the one with the largest magnetic sensitivity;
5. this line is rather ``clean'' in most stars: on the red side, it is free from any strong blend in almost all the studied stars. On the blue side, it is often blended by one (or in some stars, possibly two - see e.g. the spectrum of HD 93507 shown below in Fig. 3 (click here)) unidentified line(s). But in most cases this blend is relatively weak, and it can be handled adequately in the measurement procedure (see below).

The main drawback of the use of   is that it is not formed in a regime of pure Zeeman effect, but rather in a regime of partial Paschen-Back effect. Indeed, the lower level of the transition responsible for it and the lower level of the transition from which   originates belong to the same spectroscopic term, and their separation is not much larger than the magnetic splitting induced by fields of kilogauss order. The magnetic field induces a mixing of the lower levels of the two considered transitions, and as a result a distortion of the profiles of the split lines   and  . These lines become asymmetric, the former with the red split components deeper than their blue counterparts, while the red component of   is less deep, but broader than the blue one. This can be seen in Fig. 1 (click here) as well as in many of the plots of the spectral region of interest illustrating this paper. A detailed study of the physics of the formation of the lines   and   has been presented in Paper I. The most relevant result, within the present framework, is that for fields up to a few tens kG, Eq. (1) keeps giving an excellent approximation of the wavelength separation of the split components of the doublet  \ (see also Sect. 6), even though their intensities may become very different in strong enough magnetic fields.

In Eq. (1), and are the wavelengths of the centres of gravity of the split components of  . In practice, these wavelengths were determined either by direct integration of the whole component profiles or by fitting a gaussian simultaneously to each of them (see Paper II for details). The latter method was preferred for lines that are not fully split, in which the magnetic components are (almost) symmetric. The direct integration works better when the splitting is large and the split components are distorted (e.g. by rotational Doppler effect). Of course, all the intermediate situations between the two extreme ``ideal cases'' described above are encountered in practice, and some compromise must be adopted. With the experience of the several hundreds of measurements reported here, most of which were repeated several times, we believe that we have developed the ability to choose the ``best'' measurement method, which has allowed us to obtain a homogeneous set of accurate data. In support of this, it may also be mentioned that, in a number of cases when both measurement techniques appeared equally suited, the results given by both of them were quite consistent. Finally, the gaussian measurement technique proved very handy to remove the contribution of the blue blend to  : whenever possible, a multiple fit of three of four gaussians was performed: one for each of the split components of  , and one or two to account for the blending line(s).

It is not straightforward to estimate the measurement uncertainties. This, in fact, is best done calling to a posteriori arguments. The discussion of this point is therefore postponed to Sect. 6.