With efficient filters for cascade effects, one can accurately determine individual transition probabilities from lifetimes derived in observing the fluorescence following laser excitation. In iron group or other complex spectra with their hundreds or thousands of lines, this method is not practicable and the astrophysicist has to take recourse to Internet databases containing bulk data. However, many values available so far and collected e.g. in NIST compilations (Martin et al. 1988) and databases from NIST, Kurucz and Kelly, are accurate to about 50%. Naturally, the data in these databases are not independent. Sometimes the NIST compilation contains experimental data but in many cases semi-empirical calculations are employed. It is hard to give error bars on this type of calculation, and if they are there at all, they are hard to substantiate.
In view of the above, it is necessary that more data become available to enable the experimentalist to decide on the real accuracy of the methods.
Our study of transition probabilities in the iron sequence using orthogonal
operators is started with Ti III
and V IV. These ions were chosen because the ground configuration
contains two d-electrons, which means that they are the first ions with
two particle (dd and dp) magnetic effects. In the III- and IV-spectra the
configurations are relatively well separated in comparison with the I-
and II-spectra
in which the energies of the 3d- and 4s-electron are competitive. On
the other hand the odd system is not yet perturbed by the open 3p-shell,
giving rise to a 
configuration. This
effect occurs in the VI-spectra and is probably already influencing the
V-spectra of the iron group elements.
To calculate the (
) 
3d4p transitions properly,
it was necessary
to take into account the interaction
with neighbouring configurations. For that reason the even system was built
from (
) and the odd system
from (
).
Interactions with other (far-lying) configurations are taken into account by
means of so-called effective operators.
These sets of configurations are almost the same as the ones used
by Wyart (1975). However he used the conventional method and
his investigation was limited to energy values without the calculation of
transition probabilities.
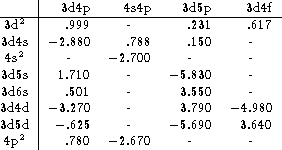
Table 1:
Values for the electric dipole transition integrals
in Ti III calculated by means of MCDF including core polarization
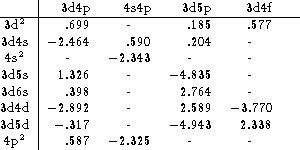
Table 2:
Values for the electric dipole transition integrals
in V IV calculated by means of MCDF including core polarization
After completing the fitting procedure, eigenvalues and eigenvectors are obtained from the diagonalization of the Hamiltonian. The eigenvectors yield the composition of the actual state in terms of pure SL-coupling, i.e. the SL-term fractions. They are used to transform the pure SL-transition matrix into the factual transition probabilities in intermediate coupling. The angular part of the SL-transition matrix is calculated from straightforward Racah algebra, the radial transition integral is obtained from the MCDF program (Parpia et al. 1996). The values of these integrals corrected for core polarization are given in Table 1 (click here) for Ti III and Table 2 (click here) for V IV.
In the Tables 3 (click here) and 4 (click here) the 
values for the
(
) 
3d4p transitions are given for Ti III and V IV,
respectively. This system is selected by cutting off the higher energy
values of both the even and the odd system in the final printing procedure
(not at an earlier stage of the calculation, as this would have influenced
the results). The first column of these tables shows the wavelength obtained
from the energy differences between the experimental level values.
Wavelengths below 2000 Å are given as vacuum wavelengths and
above 2000 Å\
as air wavelengths. The second column
gives the log(gf) values followed by the J-value, energy value and the
name of the level of the lower (even) level. The first character of the
level name designates the configuration number: for the even levels
"1" refers to 
and "2" to 3d4s; for the odd levels "1" refers to
3d4p. An "*" after the energy
value indicates that the level is known, in which case (all cases here)
the experimental level value is given. When unknown, the calculated
energy value is given and used to calculate the wavelength. In the latter case,
the wavelengths could deviate and one should be very cautious
to use them for stellar spectroscopic assignments.
The electric dipole intensities are compared to those in Kurucz's database
(Kurucz 1993) which is at present the most extended data base
for transition probabilities.
Although in many cases the results from Kurucz are comparable to ours,
there are also a number of cases where large discrepancies (some orders of
magnitude for the transition probabilities) occur.
Striking examples of these differences are given in Tables 5 (click here) and
6 (click here) for
transitions in the 
and 
transition
array respectively. In these tables not only the differences between
Kurucz's and our work are given but also the intensity numbers from the
original analysis by Edlén & Swensson (1975). These
relative intensity numbers are based on visual estimates on a scale 0-25
and comparable (on a different scale) to the intensity numbers given in the
NBS compilation (Kelly 1987). From the tables it seems that
our values fit the experimental data better.
Apart from allowed electric dipole (E1) transitions, many stellar objects show spectral lines due to magnetic dipole (M1) or electric quadrupole (E2) "forbidden" transitions that occur within complexes of the same parity. These spectral lines can only be observed when other means of decay, like E1 or non-radiative collisional transitions are unlikely, implying a low excitation temperature. Therefore, only forbidden lines in the ground state (even) system are relevant.
For the magnetic dipole transitions only an angular part, that depends on
the S-, L- and J-values of the initial and final states, exists. For
the electric quadrupole transition, however, the transition probability
contains, apart from the angular part, also a radial part. Just as in the
case of the electric dipole transitions this radial part was calculated from
the MCDF wavefunctions. In Tables 7 (click here) and 8 (click here) the
radial integrals for the electric quadrupole transitions are given. The
tables are given in the form of a symmetric matrix since the 
integral is the same as the
integral (in both cases a 
transition is
calculated). The table is somewhat complicated by the fact that for
E2-transitions within the 3d4d (or 3d5d) configurations, there are two
non-zero operators, one for the 
and one for the 
(or
) transition. For these cases, there are two rows in the table:
the upper one gives the 
integral and the lower the 
(or 
) transition integral.
Tables 9 (click here) and 10 (click here) give the A-values for the forbidden
lines. Just as for the
allowed lines only transitions involving 
and 3d4s levels are
included. The listing is in wavelength order.
The level with the lower J-value is given first in the designation of the
transition.