Since the calibrations used in each region are different, systematic differences in computed colour excesses or distances could be present. The application of the algorithm to stars from open clusters was used as a test of the continuity and agreement among the various calibrations.
The supergiant stars with photometric data belonging to open clusters were used to build the calibrations and so there are no independent data to test them. Thus, the present analysis has been restricted to the main sequence regions.
The open clusters were selected from the Open Cluster Data Base (Mermilliod 1992).
About 60 clusters have more than
20 stars with 
.
Among the "normal" (in the sense described in Section 2.3)
stars in the field of an open cluster we selected
the "photometric members": E(b-y) and distance modulus were computed for
each star together with the mean and standard deviation (
) for each
cluster.
A star was considered a member of the
cluster if its E(b-y) and its distance modulus were both inside the
interval
mean 
. In some cases, two or three
iterations were needed until the
result was self-consistent. In the case of Mel 20 (
Per), Mel 22
(Pleiades) or Mel 25 (Hyades) we also consulted the published list of members
(Prosser 1992; Van Leeuwen et al. 1986; Schwan 1991).
This procedure was applied to main sequence stars belonging to photometric
regions 1-4 (O-G2 type stars). A star in region 5 was considered a member
if being dereddened using the mean E(b-y) of the cluster, its 
was in agreement with its spectral type and its distance modulus was
compatible with that of the cluster. The reason for this different treatment
is the provisional character of Olsen's (1984)
calibration, which might disturb the selection of members for the other regions.
After the selection of members, the stars in region 5 were dereddened with
the algorithm.
The final sample was formed by those clusters satisfying the following criteria:
Furthermore, we rejected six clusters (NGC 129, NGC 1342, NGC 1502, NGC 7039,
NGC 7062 and IC 4756) that showed very large discrepancies among
regions or very high standard deviations in the values of E(b-y) or
. These were probably due to strong differential
reddening or misclassification of members.
The final sample contained 24 open clusters and 841 stars, listed in Table 9 (click here) in ascending order of age. The number of accepted members in each main sequence region is also shown in the table.
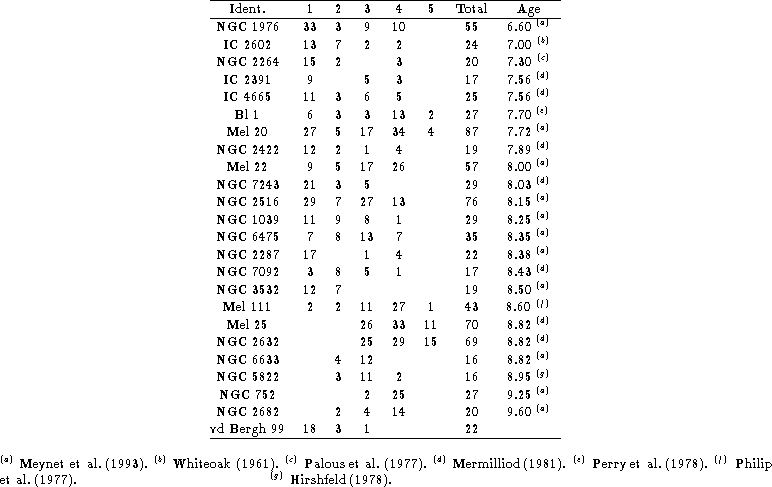
Table 9: Selected open clusters and number of "photometric" members in
each Main Sequence photometric region
In analyzing all the clusters together, for each star we computed the difference between the individual E(b-y) and the mean E(b-y) for the corresponding cluster. The analogous difference was computed in the case of distance modulus. Table 10 (click here) shows the mean of these differences for each region and the corresponding standard deviation.
Variance analysis shows coherence at a significance level of 95% between the reddening values computed for the late regions (3 and 4), and statistically significant differences for reddenings computed for regions 1, 2 and 5. The differences decrease by removing NGC 1976 and NGC 2516 clusters from the sample. NGC 1976 is the youngest cluster in the sample with cool stars placed above the ZAMS, which could be pre-main sequence stars. If the E(b-y) for these stars was inaccurate this would artificially introduce a large difference with the reddening of the early region. A large reddening scatter has been reported by several authors (see for example Snowden 1975) for NGC 2516. This scatter can interfer with a right choice of photometric members and might explain the discrepancy among regions.
The use of other calibrations (Hilditch et al. 1983 or Claria 1974) for the intermediate region does not improve the results. The differences are practically the same. The mean differences in region 5 are of the same order as those in other regions, but with a higher standard deviation.
The difficulty in selecting members accurately, the presence of pre-main sequence or unknown binary stars or the differential reddening are several factors that contribute to the differences among regions, which, in any case, are lower than the internal errors associated with the calibrations. Taking these facts into account we can conclude that there is good coherence among the calibrations used.
For the distance modulus, variance analysis
shows coherence among regions 3, 4 and 5
and between regions 1 and 2, but statistically significant differences between
these two groups.
The differences among regions are lower than the accuracy
of the calibrations, which take in from 0.2
for A-type
stars to 0.5
for early B-type stars.
It should be borne in mind that an error in E(b-y) causes an error
in the determination of 
equal to 
and also in the distance modulus. It is easy to verify from Table
10 (click here) that this induced error in 
is smaller than the
discrepancies among regions.
So, the differences are mainly
due to disagreements in the absolute magnitude calibrations.
The calibrations for
the cooler stars were mainly built from trigonometric parallaxes of nearby
stars while for the early and intermediate regions they were
based on star members
of open clusters. As the former calibrations are more accurate, we propose
correcting the absolute magnitude of the early and intermediate regions,
in such a way that the differences quoted in Table 10 (click here)
disappear.
Table 10: Mean values of 
and 
in the sense 
,
and the same for 