Cas
Cas in the continuum
The interpretation of the visibility points follows a simple model for 
Cas
where we consider the continuum source as a superposition of a central star and
an extended circumstellar envelope. According to spectrophotometric estimates of
Cas, the underlying photosphere of this object has an angular diameter of
.45 mas (Ochsenbein & Halbwachs 1982) almost unresolved in the range of baselines
achieved during this study. Formally, we estimate the equivalent uniform
disk
angular diameter of the envelope from the following model for the
visibilities:
is the calibrated visibility at the spatial frequency u. 
is a
normalization factor taking into account the attenuation of the zero baseline
visibility by the GI2T (Mourard et al. 1994b). 
is the Bessel function
of first degree. 
and 
denote the equivalent uniform disk
angular diameters of the star and the envelope in milliarcsecond and
C=1/65650000 a conversion constant between u and 
. The fluxes 
and
of the star and the envelope are taken as .85 and .15 relative to the
continuum emission at 660 nm according to Stee et al. (1995). This is obtained by
considering the continuum photons of the extended envelope from free-free,
free-bound emission and the scattering of the photospheric light in agreement
with the models for 
Cas (Poeckert & Marlborough 1978; Stee et al. 1995).
Note that we used the visibility model from Eq. (3) to interpret the
visibilities for different polarizations. 
, 
and
which correspond to the visibilities in natural, linearly polarized parallel
and perpendicular to the baseline respectively.
Figure 3 (click here) displays the visibility points in natural light and in linear
polarizations as a function of the baseline according to Table 2 (click here). The gap of
visibilities at short baselines under 22.05 meter is due to the dimensions of
the central hub of the GI2T which limits the minimum distance between the
telescopes. This problem is overcome by setting the normalization factor
as a free parameter of the model so as to obtain 
/
.
Finally we fit 
in natural light by minimizing the 
function between model and observed visibilities from Eq. (3) and Table 2 (click here).
We find 
mas where the error on the angular
diameter is obtained by differentiating 
with respect to 
.
This error takes into account the actual estimate of photon
noise in computed power spectra (Eq. 2) and assumes that each
's is an independant sample of the spatial power spectrum of
Cas measured by the GI2T.
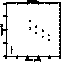
Figure 3: Calibrated visibility points on 
Cas as a function of baseline.
The visibilities are given in % in the range of 40% to 80% for displaying an
eventual variation of the visibilities related to polarization states (natural
light: squares, linear parallel to the baseline: diamonds, polarized perpendicular
to the baseline: triangles). The average error is given on the bottom-left of the
plot
Cas in linearly polarized light
We applied the model of the previous section to the visibility points obtained in the
two linear polarizations (Table 2 (click here)). We found
mas
and 
mas. By inspecting Fig. 3 (click here) one notes
an apparent trend of 
visibilities (triangles) respective to 
and
which have a larger dispersion. We think that our limited accuracy on
the visibilities (bottom-left of Fig. 3 (click here)) can only set an upper limit to
the ratio of these diameters by taking their maximum and minimum values at one 
,
namely:
Using 2D gaussians models to check a difference of flattening or major axes of elliptical envelopes in polarized light led us to the same conclusion. Note that in its present state -fixed north-south direction of resolution of the GI2T, our simple polarimetric experiment might miss detecting polarization effects in the envelope of gamma Cas if it happened to present special morphologies. Thus, for an unambiguous interpretation of such observations one would need other directions of resolution by adding a third telescope in the East-West direction or/and by using Earth-rotation synthesis. Also and ideally one could measure the whole set of Stokes visibilities in order to reconstruct or to model-fit intensity maps according to the classical definition of Stokes parameters (Shevgaonkar 1987).