From the spectral energy distributions and from the response functions
of the filters in the various bands, the K and EC corrections
have been computed; they are presented in Tables 31-38.
The corrections have been computed up to z=3 for the bands
of the Johnson's photometric system (
and
corresponding to 
and 
from Buser (1978) and 
from Bessel & Brett 1988) and gri
of the Thuan & Gunn system (1976) as modified from Schneider et al. (1983).
The B magnitude is computed considering the sum of the two filter response
functions 
and 
divided by two.
Being 1000 Å
the lower limit of the wavelengths considered from the model,
the U and B bands have been computed respectively up to
z=2 and z=2.5.
The response function of the filters are given in Tables 39-41; it is useful to underline that, due to a typing error in Table 4 from Bessell and Brett, the definition of the H and K bands can be ambiguous. It is indispensable, in any case, to check the response function of any filter of interest; in the case of the K band, the difference between the filter here adopted and that in the figure of Bessell and Brett can give rise to errors in the corrections of 0.2 maximum.
The spectral energy distributions of the models of
different Hubble types of age 15 Gyr
are given in the Tables 3-5 for the E, Sa and Sc
in the spectral range 
Å. The SEDs are also presented in
Fig. 1 (click here).
From top to bottom (at 1000 Å) the spectra of the Sc, Sa, E2 and E
are shown; it is visible that the difference
between the spectra of the two ellipticals is significant only at the shortest
wavelengths. The rest frame spectra of evolving SEDs of different ages
are presented in Fig. 2 (click here) (E), Fig. 3 (click here) (Sa) and Fig. 4 (click here) (Sc); the ages
shown are 15, 13.2, 10.6, 8.7, 7.4, 5.9, 4.3, 3.4 and 2.2 Gyr,
corresponding respectively to the redshifts: 0, 0.1, 0.3, 0.5, 0.7, 1.0,
1.5, 2.0, 2.5, 3.0. Such SEDs are given in Tables 6-29, from which the
interested user can compute any desired property.
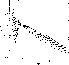
Figure 3: SEDs of the Sa model for the same redshifts of Fig.
2 (click here)
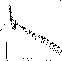
Figure 4: SEDs of the Sc model for the same redshifts
of Fig. 2 (click here)
Considering the high metal content adopted and the observed
correlation between the 
index and the absolute luminosity,
the elliptical model is representative of luminous objects. Due to the
observed substantial variations of the ultraviolet flux with the
galactic luminosity, the results presented here cannot be applied
to low luminosity ellipticals (i.e. with a lower metal content)
for redshifts 
.
Furthermore, the differences between the two model ellipticals
(
and 
Gyr) appear significant starting from
z=0.6 (K correction) and z=0.20 (EC correction) in the bluest bands.
In order to obtain the observed colour of the progenitor galaxy of a given type of local galaxy the following relation can be used:
observed colour=colour of the local corresponding galaxy + (difference between the K corrections of the first and the second band)+ (difference between the EC corrections of the first and the second band).
This relation can be deduced from Eq. (3). For instance, if one wants to compute the expected observed colour (V-J) of an elliptical at z=1:
colour of a local elliptical (V-J)=2.25
, 
, 
expected observed colour=2.25+3.14-0.91=4.48.
Figures 5-15 show the K and EC corrections for different bands; the sudden change in all the curves at z=2.5 is due to the fact that the last two models have been computed with a large redshift step (0.5). Considering the smooth behaviour of these functions between a redshift 2.5 and 3, a smaller redshift step is not required.
Figures 16-23 show the rest frame and observer's frame colour evolution.
In Table 30 model 
corrections are compared
with those of Pence for negligible Galactic extinction.
The differences, starting at relatively low redshift for the
latest types, are partly due to the slightly dissimilar response functions
adopted and mainly to the differences in the SEDs.
It must be stressed that two galaxies classified of the same type on the basis
of their morphological appearance (spiral arms, bulge to disk ratio
etc.) can have significantly different spectra,
indicative of unlike present and past star formation rates.
Therefore the model galactic sequence should be interpreted as a
``star formation'' sequence, while the results found with an empirical method
will necessarily depend on the single galaxies chosen for the sample.
For this reason the comparison of the two methods results rather difficult.
Furthermore Pence himself defined the ultraviolet observations available to him
(preliminary OAO data) as ``somewhat uncertain'', especially for E/S0.
Moreover, due to the lack of ultraviolet
observations for the Sbc, Pence had to interpolate between the types Sab
and Scd. Coleman et al.'s results for bulges are in
agreement with elliptical results from Pence until a redshift 
in the V band. They found instead substantial differences from Pence
in the 
of the elliptical for z>0.3, probably due to the
UV Pence's difficulties mentioned above. A better agreement is obtained
between their results and the model values presented here.
Figure 6: 5-15 : K and EC corrections:
the solid line represents the elliptical with e-folding time 1 Gyr;
the dotted line the elliptical with 
Gyr (E2); the short dashed
line refers to the Sa and the long dashed line to the Sc. In some cases the
curves of the two ellipticals are superimposed and therefore indistinguishable.
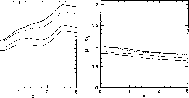
Figure 17: 16-23 :
Rest frame and observer's frame
colour evolution: the former case is
denoted by the ``0'' subscript. Symbols as in Figs. 2-12.
