We modelled the planetary nebula populations in galaxies in two steps. The first step was to model the evolution of the host galaxy. This was done using the galaxy modelling code described in Arimoto et al. (1992). This code tracks the consumption of gas, the interstellar medium metallicity, and the numbers of stars formed as a function of time. The second step was to use these data to compute the resulting planetary nebula population, which was done using a code developed specifically for this purpose.
The galaxy modelling code is well known and has been amply described in the literature (see Arimoto & Yoshii 1986 for the fundamentals; Arimoto et al. 1992 for subsequent changes). This code divides a galaxy into two parts, a region where star formation occurs and, if gas inflow is allowed, a separate gas reservoir in which no star formation occurs. The basic premise of the code is that, as stars form, they deplete the pool of material available for subsequent star formation. Every stellar generation locks matter into long-lived stars, but each also enriches the interstellar medium in heavy elements by returning processed material from supernovae. This code only implements enrichment from classical type II supernovae (i.e., core collapse in massive stars). As a result, its treatment of oxygen is correct, at least at low metallicities (cf. Maeder 1992), but that of iron is only approximate due to the lack of other supernova sources. A basic assumption is that the interstellar medium is always well mixed, so that abundances are uniform throughout and each stellar generation is formed with zero abundance dispersion. At each time step in the evolution of a model galaxy, typically 5 million years, the gas mass fraction, the metallicity of forming stars, and the mass of gas transformed into stars are recorded.
The galaxy models were intended to be very schematic. The
galaxies were initially entirely composed of gas with zero metallicity and no gas
infall was allowed. Unless specifically noted below, all models use a Salpeter
(1955) initial mass function, i.e., 
, where
m is the stellar mass and k is a normalization constant defined such that
the integral of the initial mass function is unity. For this project, the only
significant modification that was made to the galaxy modelling code was to
implement tracking of the interstellar medium oxygen abundance.
A separate code, called the planetary nebula population code (PNP
code), was developed to compute the global properties of a galaxy's planetary
nebula population. The planetary nebula population comprises the planetary
nebulae produced by each stellar generation that is old enough to produce
planetary nebulae, i.e., age 
. At each time step, the
galaxy modelling code records the mass of gas turned into stars, the metallicity
of these stars, and the oxygen abundance in the interstellar medium. The PNP
code uses these data for each generation of stars to predict the luminosity
function and the mean oxygen abundance for the planetary nebula population.
Since these global properties are calculated from the abundances and luminosity
functions for planetary nebulae in each stellar generation, the discussion that
follows focuses upon this process within a single stellar generation.
The PNP code uses stellar
lifetimes based upon the stellar evolution models of Bressan et al.
(1993) and Fagotto et al. (1994a,b). These models are
attractive because they span wide mass and metallicity ranges, they are based
upon recent opacity calculations, and they incorporate homogeneous input
physics. In addition, these models are evolved to the early AGB phase, so
there is negligible error in using their lifetimes to that point as their
total lifetimes. These stellar lifetimes differ from those used by the galaxy
modelling code (Arimoto & Yoshii 1986), but these more realistic
lifetimes are necessary to correctly predict the rate at which each stellar
generation produces planetary nebulae (e.g., Renzini & Buzzoni
1986). For these stellar models, the dividing mass between those stars
that go on to become supernovae and those that become white dwarfs is between
and 
. Here, all stars with masses below 
are assumed to become
planetary nebulae.
For any single stellar generation, its age and metallicity fix
the initial masses of its planetary nebula progenitors. At any particular epoch,
the mass range for the planetary nebula progenitors in any stellar generation is
fixed by the nebular expansion rate, since this determines how long the planetary
nebulae remain visible. Planetary nebulae are assumed to be visible so long as
their densities exceed 
.
Now, knowing the initial masses of the planetary nebula progenitors, the PNP code integrates the initial mass function over the appropriate mass range to determine the mass fraction of this stellar generation that is producing planetary nebulae. The total number of planetary nebulae from each stellar generation is then
Given the
initial masses of the planetary nebula progenitors in each generation, we
assign a planetary nebula central star mass, 
, according to an
initial-to-final mass relation
where 
is the initial mass of the
planetary nebula progenitor. We determined a and b by comparing the PNLFs
from the models with those observed in real galaxies.
The PNP code models the
evolution of planetary nebula central stars by interpolating the evolutionary
tracks for the hydrogen-burning models of Vassiliadis & Wood
(1994). Fortunately, it is not necessary to interpolate the
Vassiliadis & Wood (1994) models directly, as their
temperature and luminosity evolution are completely characterized by the
core mass, 
, and the time, 
, to evolve from a
temperature of 
to the maximum temperature. Consequently, it
is possible to define scaling parameters, which are functions of 
and 
, that transform the evolutionary track for central
stars of any mass into a ``normalized" evolutionary track. Using the
normalized temperature and luminosity evolution as a function of time, in
units of 
, the temporal evolution of a central star of any
mass may be calculated by re- scaling the normalized temperature and
luminosity according to the value of 
. The evolutionary tracks
are only followed to a time of 40 000 years after the central star reaches
a temperature of 
. None of the planetary nebulae in our models
is visible for times longer than this.
Figure 3 (click here) shows several of the Vassiliadis & Wood (1994) models along with the corresponding tracks calculated according to the scheme outlined above. Note that the interpolated tracks are calculated for the same time points as the Vassiliadis & Wood (1994) models. The tracks in Fig. 3 (click here) are labelled according to the mass of the central star. As this figure demonstrates, the predicted time variation of the luminosity and temperature are in good accord with the models of Vassiliadis & Wood (1994).
Figure 3: A comparison of the Vassiliadis & Wood (1994) models with those computed
by the PNP code. The PNP code points are calculated for the same times as the
Vassiliadis & Wood (1994) models. Central star evolution is followed for 40 000
years from the time the temperature attains 10 000 K
luminosities
Once the
luminosity and temperature of its central star are known, it is relatively
straightforward to calculate the 
luminosity of a planetary
nebula's shell. The energy distribution for the central star is approximated
by a blackbody flux distribution (see Gabler et al. 1991 for
justification). Given the central star temperature, T, the data in
Allen (1973) were interpolated to calculate the fraction,
, of photons emitted by the star that are capable of ionizing
hydrogen:
where 
. For a
blackbody, the total number of photons emitted can be written as
(Allen 1973) where L is the stellar luminosity and 
is the Stefan-Boltzman constant. In ionization equilibrium, the rate of
recombinations must equal the rate of emission of ionizing photons, so the
luminosity can be determined via (e.g., Osterbrock
1989)
where 
and 
are, respectively, the effective recombination
coefficient for the 
line and the hydrogen recombination
coefficient summed over all levels except the ground level (Case B).
is the nebular electron temperature. We adopted the values of
and 
for a temperature of
from Osterbrock (1989).
The nebular mass and the optical
depth to ionizing photons modify the 
luminosity, however. The
nebular geometry is assumed to be a filled spherical shell. The mass of
this nebular shell, 
, is either a fixed maximum of 
or the difference between the progenitor's initial mass and the
mass of the central star it produces, whichever is smaller. Whether this
nebular mass is sufficient to absorb all of the ionizing photons from the
central star depends upon the nebular expansion velocity, V, for this
fixes the nebular density, 
. At any time, t, the nebular density
is given by
where 
and 
are the
initial radius and density of the nebulae. The initial radius was chosen
arbitrarily, while the initial density was fixed by considering the typical
values of the 
luminosity, electron density, and expansion
velocity of bright planetary nebulae in the Magellanic Clouds. Based upon
the complete sample, 
, 
and 
are typical for the
brightest planetary nebulae in the Magellanic Clouds. For a uniform
density nebula,
which yields a typical
nebular volume of 
, or a typical radius of
(0.07 pc) for a spherical nebula. For
, this radius is achieved after 
. Given this time, solving Eq. (7) for 
yields the
initial density given above. The mass that the central star may ionize,
, is given by re-arranging Eq. (8), noting the relationship
between mass, volume, and density
When
the density is sufficiently low that 
, the
nebula only absorbs the fraction 
of the
central star's ionizing flux.
Once the 
luminosity is
known, assigning an 
ratio fixes
the 
luminosity. For a planetary nebula whose
central star's temperature exceeds 
, 
is set to the maximum value
appropriate for the nebular oxygen abundance, 
, given by Eq. (3) of RM95.
For central stars with temperatures between 
and
, the value of 
given by the prescription for hotter stars is reduced by a factor of
to be
consistent with the observed correlation between central star temperature and
(Kaler & Jacoby 1991;
Méndez
et al. 1993). This reduction factor accounts for the lower 
ratios that occur while the central stars are
evolving from low to high temperatures. The 
ratios for planetary nebulae whose central stars are cooler than 
are set to zero.
Given the high initial density, there are occasions when emission
of 
is quenched by collisional de-excitation.
We have implemented this correction according to
(Osterbrock
1989) where 
is the rate of collisional
de-excitation per unit volume and 
is the spontaneous
de-excitation coefficient. We adopted the definitions and values
for these quantities from Osterbrock (1989).
The PNP code uses two 
ratios: a mean value when calculating
the luminosity function, and a maximum value when determining the PNLF
peak luminosity. When calculating the PNLF peak luminosity, the 
ratio, either 
or the modified
value from Eq. (10), is used directly. When calculating the
luminosity function, the mean 
ratio for that oxygen abundance is more appropriate, so the maximum
ratio, either 
or the modified
value from Eq. (10), is reduced by 0.145dex (see RM95 for details).
The PNP code follows the
temporal evolution of planetary nebulae from each stellar generation
through the H-R diagram and, using the maximum 
ratio, notes the maximum 
luminosity from each generation. The largest sets
the maximum 
luminosity for the entire
population.
Next, using the average 
ratio, the PNP code evolves the planetary nebulae from each
stellar generation through the H-R diagram and determines the time
intervals during which their luminosities are within 1, 2, 3, 4, and
5 mag of the maximum 
luminosity (the
luminosity thresholds). Dividing these five time intervals by
the planetary nebula lifetime yields the fraction of their lifetime
that the planetary nebulae spend above each luminosity threshold.
Since planetary nebulae from a single generation will occupy all
possible stages of evolution at any time, the fraction of planetary
nebulae with luminosities above any particular threshold is equal to
the fraction of their lifetime spent above that threshold.
Multiplying the total number of planetary nebulae in this generation
by the fraction above each luminosity threshold then gives the actual
number of planetary nebulae above each threshold for that generation.
To obtain the luminosity function for the entire planetary nebula population, the process just described is repeated for all stellar generations. The total number of planetary nebulae above each luminosity threshold is then just the sum of the number from each stellar generation. Compared to Monte Carlo-type algorithms, this method is very efficient for computing the luminosity function for a planetary nebula population. However, it is a ``high signal-to-noise" method in the sense that it does not allow for the fluctuations that occur when small numbers of planetary nebulae are involved.
Once the number of planetary nebulae above each luminosity threshold from each stellar generation are known, the mean abundance and its dispersion within each luminosity bin are calculated.
Throughout this
description of the PNP code, we have omitted a complication that
occurs in real galaxies: stars of a given age in real galaxies do not
all have the same metallicity (e.g., Boesgaard 1989;
Rana 1991). The PNP code was designed to allow for
an arbitrary metallicity dispersion among the stars formed within a
single stellar generation, and simulates the effect of a Gaussian
abundance dispersion by splitting the planetary nebula population
from each stellar generation into three sub-generations. All
planetary nebulae within 
of the mean, 68% of all
objects, are assigned the abundance from the galaxy code. The
remaining planetary nebulae are assigned abundances 
above and below the mean, which is the weighted mean
deviation for points beyond 
. The high and low
abundance subsets each account for 16% of the planetary nebulae
from each stellar generation. An intrinsic abundance dispersion of
0.13dex within each stellar generation was chosen. This is of the
same order of magnitude as the observed abundance dispersion among
bright planetary nebulae in the Magellanic Clouds
(Table 2 (click here); see also Sect. 4).
Two sequences of
model galaxies were calculated. The models in the first sequence, the
star-forming sequence, were designed to schematically represent the
LMC, the SMC, and the disk of the Milky Way. The four models in this
sequence form stars at a constant rate. Their star formation rates
were chosen such that their final interstellar medium oxygen
abundances spanned the current abundances observed in the Magellanic
Clouds and the disk of the Milky Way. The second sequence, the
elliptical sequence, emulates the conditions in ellipticals. Most of
these models turn various fractions of their initial mass into stars
during an initial burst of star formation, and then evolve passively,
i.e., without any further star formation. The remaining elliptical
models undergo a second burst of star formation 10 Gyr after the
beginning of the first. All models were evolved to an age of
15 Gyr. (Age is the time elapsed since the beginning of star
formation). All of the model galaxies have initial gas masses of
except the LMC and SMC
models, which have initial gas masses of
and 
respectively (Lequeux 1984; Russell &
Dopita 1992).
The parameters of the LMC model and one of the elliptical models calculated according to the prescription outlined thus far are tabulated in Table 3 (click here). (The elliptical model is model R2 from Table 4 (click here). Further details will be given below). For comparison, the observed parameters for the LMC and the Henize & Westerlund (1963) distribution (as modified by Ciardullo et al. 1989b), are also tabulated. Note that the first 2 mag of the LMC PNLF in Table 3 (click here) was defined using the LMC's global PNLF, whereas the Jacoby PNLF was used to define the remainder of the LMC PNLF. The interstellar medium oxygen abundance quoted for the elliptical models is the last epoch oxygen abundance, i.e., the oxygen abundance when star formation ceased. For the LMC models, the oxygen abundance is the abundance attained in the interstellar medium at 15 Gyr. For the planetary nebulae, we tabulate the mean oxygen abundances for objects within 1 mag of the PNLF peak and for those with luminosities between 1 and 2 mag below the peak. We normalized the cumulative PNLFs at 3 mag from the PNLF peak, instead of 5 mag, since this reduces our sensitivity to the uncertainties in the model parameters. If our prescription of planetary nebula evolution is incorrect, the predicted cumulative number will be systematically worse the lower the luminosity threshold.
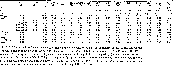
Table 3: Parameters of the planetary nebula population: Naïve
models
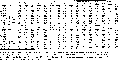
Table 4: Parameters of the planetary nebula population: Final
models
In Cols. 4 through 9,
Table 3 (click here) presents three models of the planetary nebula
populations predicted for the LMC and an elliptical galaxy. The
three models of the planetary nebula population for each galaxy
differ only in the expansion velocity chosen for the planetary
nebulae. In the LMC models, almost all planetary nebulae are
optically thin if the expansion velocity is 
,
but almost all of them are optically thick if the expansion
velocity is 
. In the elliptical models, all the
planetary nebulae are optically thin for expansion velocities of
30 and 
, but they are all optically thick if the
expansion velocity is 
.
These models demonstrate several successes and drawbacks of the simple
model of planetary nebulae described so far. First, in the elliptical
models whose planetary nebulae are optically thin (Cols. 7 and 8), the shape of the
PNLF is in excellent agreement with the Henize & Westerlund
(1963) luminosity function. Ciardullo (1995)
has shown that this luminosity distribution arises naturally from
the evolution of optically thin planetary nebulae. Second, for
the LMC model whose planetary nebulae expand at 
(Col. 4), the shape of the first 4 mag of the PNLF is in
respectable agreement with the luminosity function observed in the
LMC. This suggests that the shape of the PNLF in the LMC differs
from that of the Henize & Westerlund (1963)
luminosity function because the planetary nebulae in the LMC are
not optically thin throughout their entire evolution. Finally,
the planetary nebulae in the elliptical model are able to achieve
the PNLF peak luminosity observed in the LMC, if the planetary
nebulae are optically thick to the central star's ionizing
radiation (Col. 9). Thus, to achieve the observed PNLF peak luminosity in
ellipticals, there is no need to invoke a subset of planetary
nebulae containing more massive central stars (Sect. 2.3). This
is not surprising, for attaining the PNLF peak luminosity requires
only a modest central star mass. As has been found previously
(e.g., Dopita et al. 1992), our model planetary
nebulae attain their maximum 
luminosity
when the central star's temperature is approximately 70 000 K. By
Eq. (4), the fraction of ionizing radiation at this temperature is
0.56. Given 
and 
for the brightest planetary nebulae in the
Magellanic Clouds (RM95), and Eqs. (5) and (6), the necessary
stellar luminosity is 
or 
. According to Eq. (5) of Vassiliadis & Wood
(1994), this corresponds to the luminosity of a central
star with a mass of approximately 
. Thus, while the model of planetary nebula evolution
described so far is able to reproduce many of the observed properties
of planetary nebula populations, these properties are not
simultaneously achieved using a single set of model parameters.
There are two significant difficulties with the models in Cols. 4 through 9, and these indicate the directions in which solutions should be sought. First, the PNLF peak luminosity varies: it is too bright in the LMC models and too faint in the elliptical galaxy models. As noted above, the peak luminosity in the elliptical models can be brought into agreement with that observed if the nebular shells absorb all of the central star's ionizing radiation. Hence, their densities cannot be too low. Second, although this is not apparent from Table 3 (click here), the brightest planetary nebulae in the LMC model are much denser and have lower ionized masses than their observed counterparts. Thus, the massive central stars in the LMC models evolve too quickly compared to the nebular envelopes, whereas the low mass central stars in the elliptical models evolve too slowly compared to the nebular envelopes. This evolution time scale difficulty may be addressed in equivalent ways through either an expansion velocity law that depends upon the central star mass or an adjustment of the central star evolution time scales. However, neither of these solutions will eliminate the already overluminous planetary nebulae in the LMC models, unless the expansion velocities or evolution time scales are large enough to make the planetary nebulae optically thin.
There are two obvious possibilities for
reducing the luminosities of the planetary nebulae in the LMC models.
The nebulae could be optically thin. It is possible to devise a
relation between expansion velocity and central star mass such that
the maximum 
luminosity achieved is equal to
that observed in the LMC. However, the PNLFs for such LMC models are
too steep, being very similar the PNLFs for the elliptical models
(i.e., following the Henize & Westerlund (1963)
luminosity distribution). Another solution is to impose a relation
between central star mass (or the initial mass) and a nebular
covering factor. In this picture, more massive planetary nebula
progenitors produce more asymmetric nebulae or nebulae with smaller
filling factors. For convenience, we have implemented this
covering factor as a function of the central star mass
where 
is the
planetary nebula central star mass and we have set 
. Note that the nebular mass is not affected by the covering
factor, the matter is simply distributed asymmetrically. Columns 10
and 11 of Table 3 (click here) present the same LMC and elliptical
models as Cols. 4 and 7, respectively, but implementing a covering
factor as given by Eq. (12). Adding a covering factor only
affects the LMC model since almost all of the central stars in the
elliptical model have masses below 
. For the model
of the LMC, adding the covering factor reduces the PNLF peak
luminosity to roughly that observed.
The brightest planetary nebulae in the LMC model (Col.
10) still have higher densities and lower ionized masses than are
observed, while the planetary nebulae in the elliptical model (Col.
11) are still too faint. Both of these problems may be addressed
through an expansion velocity law. After much trial and error, we
found that the properties of the brightest planetary nebulae in the
LMC model matched those observed if their expansion velocities
allowed them to begin leaking ionizing photons shortly after
attaining their maximum luminosity. (Here, and in the following,
leakage of photons refers to those directions in which there is
matter. The nebulae always leak ionizing photons over that fraction
of a sphere where there is no matter). Given the evolution time
scales of the Vassiliadis & Wood (1994) models, the
necessary expansion velocities, 
, at which the nebulae
begin leaking photons shortly after attaining maximum luminosity
are
The models shown in Cols. 12 and 13 of Table 3 (click here)
incorporate planetary nebulae with these expansion velocities. The
densities and ionized masses of the brightest planetary nebulae in
the LMC model in Col. 12 are similar to those observed. The LMC and
elliptical models also now have similar PNLF peak luminosities. The
peak luminosities differ only because the mean oxygen abundance is
higher in the elliptical model, resulting in a slightly larger 
ratio. In addition, the oxygen
abundances for the first two luminosity bins in the model of the LMC
now differ, as observed.
However, the PNLF in the elliptical model
in Col. 13 is flatter than the Henize & Westerlund
(1963) luminosity function. Its PNLF is too flat because
the planetary nebulae are all optically thick until after they
attain their maximum luminosity. We can make the PNLF steeper by
imposing a lower limit upon 
. If there is a lower limit
to 
, then, as the central star masses decrease, the
planetary nebulae begin leaking ionizing photons earlier in their
evolution. Consequently, planetary nebulae with lower mass
central stars attain lower maximum luminosities and fade sooner,
reducing the number of bright planetary nebulae and increasing the
number of faint ones, both of which make the PNLF steeper. To
allow us to vary both 
and the initial-to-final mass
relation independently, we implemented 
as a cut-off
velocity corresponding to an initial mass, 
.
Experiment showed that a cutoff corresponding to an initial mass
worked well. Models incorporating this
lower limit to 
are found in Cols. 14 and 15 of
Table 3 (click here). As expected, the PNLF for the elliptical model
is now steeper, and in good agreement with the Henize &
Westerlund (1963) luminosity function. The PNLF peak
luminosity in this model has dropped, however, indicating that
even the brightest planetary nebulae are now somewhat optically
thin to ionizing radiation. The shape of the LMC PNLF is now also
closer to that observed, though the fraction of objects in the
highest luminosity bin is still too low.
The only important discrepancy
remaining between observation and the models presented in Cols. 14
and 15 is the shape of the PNLF in the LMC model. (Note that we are
concentrating only on the first 4 mag of the PNLF). Considering the
very strong dependence of 
upon central star mass (Eq. 13),
the expansion velocities for the more massive model planetary nebulae
are very high, so their lifetimes are short. Indeed, the expansion
velocities predicted by Eq. (13) are not realistic expansion
velocities. The predicted velocities for the planetary nebulae with
massive central stars exceed those observed in the Magellanic Clouds
by over a factor of ten. (Typically LMC planetary nebulae span the
20 to 
velocity range, e.g., Dopita et al.
1988). The model of the LMC has too few planetary nebulae
in the brightest luminosity bin because the planetary nebulae
produced by the youngest progenitors evolve too quickly. The
simplest remedy is to re-map the expansion velocities to a smaller
range. Consequently, we implemented the expansion velocity law,
,
To use the expansion velocities from Eq. (14), we had to modify
the evolution time scales for the central stars by a factor of 
in order to preserve the correct density and ionized
masses of the brightest planetary nebulae in the LMC model. Although
our choice of Eq. (14) is arbitrary, it represents a compromise. As
the dependence upon the central star mass becomes stronger, the
bright end of the PNLF in the LMC model becomes steeper, and the mean
oxygen abundance for the planetary nebulae in the highest luminosity
bin increases. Equation (14) allows a good fit to both the PNLF and
the abundances for the brightest planetary nebulae. Because Eq. (14)
is much less sensitive to central star mass than Eq. (13), the
evolution time scales for massive central stars are increased
considerably while those for low mass central stars are shortened.
However, central stars of high mass still evolve faster than those of
low mass. Models incorporating these new expansion velocities and
corrected central star evolution time scales are found in Cols. 16
and 17 of Table 3 (click here). These changes have very little effect
upon the elliptical model because its central stars span such a
narrow mass range, but they modify the shape of the PNLF for the
LMC model, bringing it into excellent agreement with the observed
PNLF.
The
initial-to-final mass relation we adopted for the models in
Table 3 (click here), 
,
is steeper than that tabulated by Weidemann (1987). A
fit to his table yields 
for solar
metallicity. Our slope was constrained to be significantly steeper
than Weidemann's (1987) in order to produce
planetary nebulae near the PNLF peak in the most metal-poor
elliptical models (see Table 4 (click here)). Physically, we require a
steeper slope because the mass range spanned by our planetary
nebula progenitors is narrower than that spanned by the models
Weidemann (1987) used to derive his white dwarf
masses. Adding a metallicity term to the initial- to-final mass
relation has only a very minor effect, both within a single model
and differentially between models of different mean metallicity.
The models in Cols. 16 and 17 of Table 3 (click here) represent our final prescription for planetary nebula evolution, and it is this prescription we adopt for the models that follow. Although our models predict more faint planetary nebulae than are observed or predicted, they otherwise reproduce the first 4 mag of the PNLFs in galaxies with and without star formation, and also populate the bright end of the PNLF in the LMC model with planetary nebulae having physical properties and abundances like those observed.
The models in Cols. 16 and 17 of Table 3 (click here) are complex. To our simple initial prescription, we had to add a nebular covering factor, an expansion velocity law, and adjust the evolution time scales of the central stars. Conceivably, the covering factor could be related to the manner in which matter is lost from the planetary nebula progenitor, which is very poorly constrained by observations. Asymmetry exists in a large fraction of post-AGB stars, for their light is polarized (e.g., Trammell et al. 1994; Johnson & Jones 1991). Although the total number of objects observed in these studies is small, it would be interesting to learn whether the degree of polarization is correlated with luminosity. The need for an expansion velocity law and an adjustment of the evolution time scale for the central star amount to coordinating the evolution of the central star and its surrounding nebular envelope. Observationally, the precise form of this connection is unknown, but its existence seems likely, e.g., the correlation of expansion velocities with the central star temperature and luminosity observed for Magellanic Cloud planetary nebulae (Dopita & Meatheringham 1990). Observationally, it is straightforward to estimate the evolution time scale of the nebular shell from expansion velocities, but it is much more difficult to study the evolution time scale of the central star. In their study of the ages of central stars (most of them massive) and their surrounding nebulae, McCarthy et al. (1990) found that many nebular shells appear to be older than their central stars. To reconcile the nebular and stellar ages, they favoured slower central star evolution, arguing that massive central stars would evolve more slowly if they stopped losing mass at a fixed envelope mass instead of at a fixed effective temperature. This would lead to larger envelope masses for massive central stars, which would slow their evolution (e.g., Schönberner 1987). The large fraction of massive central stars among those studied by Méndez et al. (1992) also argues, qualitatively, that the lifetimes of these stars is not as short as models predict. Clearly, the need for a covering factor and the connection between the nebular shell and the central star represent the greatest liabilities of the models presented here. This is not especially surprising, perhaps. Quantitatively, observations provide only very loose constraints upon the way planetary nebula progenitors lose matter, how or when it stops, and whether the subsequent evolution of the central star and nebular envelope are coupled.
The
parameters for the remaining galaxy models are presented in
Table 4 (click here). The format of Table 4 (click here) is identical to
that of Table 3 (click here), though we have suppressed listing 
, 
, and the velocity law since these are all
identical to those of the final two models in Table 3 (click here).
In Table 4 (click here), there are five series of elliptical galaxy
models. The models within a single series differ from one another
by the fraction of their initial mass that they convert into stars. The model series
differ from one another by their histories of star formation. The first series of
elliptical galaxy models is the ``rapid" elliptical series (models
RX, where 
, in Table 4 (click here)).
These model galaxies formed all of their stars in the first billion
years of their existence and subsequently evolved passively. The
second series, the ``slow" ellipticals (SX in Table 4 (click here)),
is identical to the rapid series, but the models in this series
formed their stars over a 4 Gyr period, then evolved passively.
The star formation rate in the rapid and slow elliptical series
decreased exponentially with time, and was chosen so that the
distribution of stellar ages was the same in all the models in each
series. The models in the third elliptical series, the ``constant
SFR" ellipticals (CX in Table 4 (click here)), also formed their
stars over a 4 Gyr period, but at a constant star formation rate.
The models in the fourth series, the two-burst ellipticals (BX
in Table 4 (click here)), also employed a constant star formation
rate, but they formed their stars in two 1 Gyr bursts beginning at
ages of 0 and 10 Gyr. Models B1, B2, and B3, formed 50%, 33%,
and 20%, respectively, of their total stellar mass during the
second burst. The final series of elliptical models, the ``flat
IMF" ellipticals (FX in Table 4 (click here)), is identical to the
rapid series, but it was computed using an initial mass function
with a slope of -2.05 instead of the Salpeter
(1955) value of -2.35.
Inspection of the
PNLFs for the elliptical models in Table 4 (click here) shows that they
vary. We chose our model parameters so that the PNLFs for the
elliptical models with last epoch oxygen abundances between one
and two times the solar value had the same shape as the
Henize & Westerlund (1963) luminosity function (the
two-burst models excepted). On either side of this abundance
range, however, our PNLFs for the elliptical models deviate
systematically from the Henize & Westerlund (1963)
function. Observationally, the shape of the PNLF in environments
where the metallicity exceeds that in the bulge of M 31 is unknown.
As for the lower metallicity regime, based upon the data from
Ciardullo et al. (1989b), the first 3 mag of NGC
205's PNLF is in excellent agreement with the Henize & Westerlund
(1963) luminosity function. Some of the variation in the
models occurs because of limitations to the ingredients.
Principally, the abundance-dependence of the stellar lifetimes is
held constant for metallicities exceeding solar metallicity, and
the variation of the 
ratio is
fixed for oxygen abundances exceeding 
, where
the calibrating data runs out (RM95). We found that we could
obtain better agreement for the models of low metallicity
ellipticals by adopting a smaller value for 
or a
larger zero point in our initial-to-final mass relation. In
Table 4 (click here)
we present a second series of flat IMF elliptical models (the
FX b series) that was calculated with a larger value of 
, 
and their PNLFs are in good
agreement with the Henize & Westerlund (1963)
luminosity function. Our choice of 
is a compromise, allowing a reasonable fit over a wide
range of metallicity.
Although the PNLF
shape in the elliptical models depends somewhat upon the model
parameters, the abundances predicted for the brightest planetary
nebulae are not too sensitive to these parameters. Considering the
two series of flat IMF ellipticals, there is a systematic offset in
the abundances of the brightest planetary nebulae by only 
(see Fig. 5 (click here)). Similarly, had we chosen a
value of 
or our initial-to-final mass relation to
achieve a good fit to the PNLF for the low metallicity ellipticals,
the oxygen abundances for the brightest planetary nebulae in the
RX, SX, CX, and FX models would decrease by 
.
In Fig. 4 (click here),
we plot the PNLFs for the R2, S2, C2, F5, and B1 elliptical models,
which all have last epoch oxygen abundances between
. Clearly, our models predict that
the shape of the PNLF is insensitive to the history of star formation
in an elliptical galaxy if star formation ended long ago. The PNLF
for model B1 is flatter at the bright end than the other models shown
here, but it is also an extreme case, having formed half of its stars
only 5 Gyr before the present. Were the fraction of late-forming
stars smaller, as in models B2 and B3, the differences seen in
Fig. 4 (click here) would be smaller as well.
Figure 4: The PNLFs for the R2, S2, C2, F5, and B1 elliptical galaxy models (Table 4).
These models predict that the history of star formation has a negligible effect upon the
shape of the PNLF in elliptical galaxies, unless they have suffered a significant, recent
episode of star formation
Figure 5: The abundance gap for all of the models from Table 4. The dashed line is a
straight line fit to the rapid (RX) and flat IMF (FX) model series and is
given by Eq. (15). Although the abundance gaps depend primarily upon the final
oxygen abundance attained in the interstellar medium, there is also some
dependence upon the history of star formation
There are four star-forming galaxy models
in Table 4 (click here). There is a slight systematic change in the
shape of the PNLF in the star-forming galaxies as the final
metallicity increases. The reduced sensitivity of the 
ratio to oxygen abundance at high
abundance is responsible for this change in the PNLF shape.
Because the 
ratio changes more
slowly with increasing oxygen abundance at high abundance, there
are smaller luminosity differences between the planetary nebula
offspring from stellar generations of different metallicity. Thus,
a larger fraction of all stellar generations produce planetary
nebulae whose maximum luminosities fall in the highest luminosity
bin, so the PNLFs become flatter at the bright end.
These models do not fit the observed trends in planetary nebula specific density (Sect. 2.3). Observations show that the planetary nebula specific density decreases in redder galaxies. Between models of different metallicity, however, the planetary nebula specific density increases in redder galaxies. It is unclear whether this is due to a deficiency in our model of planetary nebula evolution or to modes of stellar evolution that are not included in our process of planetary nebula production. In particular, a process that prevents larger fractions of stars from producing planetary nebulae at higher metallicities, e.g., the AGB-manqué route, could help solve several problems. Such a planetary nebula ``sink" would not only help reverse the specific density trends found in our models, but it would also help to avoid the metallicity-dependent changes in the PNLF shape discussed earlier.