Great care has been taken to ensure a good calibration of the LECS. Each of the critical components has been separately calibrated and then the entire calibration has been verified at instrument level. The measurements have been performed using SSD's 6 meter X-ray beam, the Berlin synchrotron facility (BESSY), and the PANTER long-beam X-ray facility of the Max Planck Institut für Extraterrestrische Physik near Munich. All measurements reported here were performed in vacuum with the nominal voltages of -20 kV on the cell and 1082 V on the PMT.
Initial functional tests were carried out using SSD's
X-ray beam facility.
During these tests, the LECS was mounted behind a pin-hole
plate and illuminated with Al (1.49 keV) and Fe (6.41 keV) radiation from
a source located 5 meters away. The pin-hole plate consists of a
130 
m
thick Ni sheet with 1 mm diameter holes in a rectangular grid with a 4 mm
pitch.
Figure 7 (click here) shows a representative image obtained with Fe
K
illumination to illustrate the overall performance of the
LECS. The two 
Fe calibration sources are visible
in the upper left and lower right corners.
The off-axis pin-hole images are asymmetric and
extended towards the outside of the FOV. This is caused
by the penetration of 
keV X-rays into the cell gas
before absorption.
Because of the driftless design (see Sect. 2.2 (click here)), these
penetrating X-rays will give rise to lower PHA and BL values
than those absorbed directly beneath the entrance window.
In addition, the variation in viewing angle and footprint
of the scintillation light will cause the measured position to be shifted.
The dependence of mean penetration depth on energy under the LECS
nominal operating conditions is shown in Fig. 8 (click here).
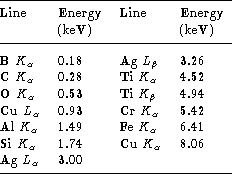
Table 2: PANTER calibration lines
Figure 7: Multi pin-hole array 6.41 keV image. The calibration
sources are the bright spots in the upper left
and lower right corners. The circles indicate the regions used for
gain mapping. The circular FOV of the LECS is approximately
bounded by the outermost pin-holes
Figure 8: Mean absorption depth in Xe as a function of X-ray energy
using the absorption coefficients of Henke et al. (1993). The positions
of the Xe absorption edges and the energies of the lines used in the LECS
PANTER calibration are indicated
The effect of penetration on the LECS event data is further illustrated in
Fig. 9 (click here). This shows
BL versus energy for incident X-ray energies just above and
just below the Xe 
edge, where there is a large discontinuity in
mean X-ray absorption depth (see Fig. 8 (click here)).
At an energy of 4.77 keV (i.e. just below
the Xe 
edge) the mean penetration depth is large and
the extended tail of events in the upper panel of Fig. 9 (click here)
towards lower
energy and BL values (1) is caused by penetration.
The events labeled as (2) are due to
multiple events occurring within the EU sampling window i.e.
event pile-up. This
feature is prominent due to the high count rates used for these calibration
measurements, but will be negligible for most astronomical sources.
In contrast, the lower panel of Fig. 9 (click here) is an exposure at
4.79 keV, i.e. just above the edge.
As expected, the effects of penetration are greatly
reduced with only a small tail towards lower energies and BL values
evident (1). In addition the fraction of escape photons
(3) has increased due to the incident photons having sufficient
energy to liberate electrons from the Xe 
shell.
A further discussion of these effects can be found in
Simons & de Korte (1989) and Bavdaz et al. (1995a).
Figure 9: BL versus PHA channel for 4.77 keV (upper panel) and 4.79 keV
photons (lower panel), i.e. just below and above the Xe 
edge. See the text for a description of the labels
A primary concern is to understand the ``gain'' of the instrument. This is the relation between the energy of an event and the mean PHA channel at which it is detected. The instrument functional tests were performed over a range of temperatures allowing the temperature dependence of the instrument performance to be investigated. The DU thermistor is used as temperature sensor, since this will be the in-orbit reference.
Each instrument functional test was divided into intervals of constant
temperature and for each
of these segments the average PHA channel of each calibration
source was determined (see Fig. 10 (click here)).
The results from the two calibration sources only
differ by a scaling factor which probably arises from a small
misalignment of the PMT and gas cell fundamental axes.
Both calibration sources show a linear dependence of gain
with temperature in the range studied.
The best-fit coefficient is -1.25% 
at a PHA channel of 410.
The scatter in the figure can be attributed to the 0.4 
resolution of the temperature measurement in
the region around 
. The same procedure was performed
using Fe 
and Al 
data from within the FOV to confirm that
the temperature dependence is independent of both position and energy.
The temperature dependence of the gain can be
corrected for by defining a nominal calibration source PHA
channel of 410 and normalizing all energy signals to this. If
the original energy channel = PHA, then the corrected channel is given
by:
where cal
and cal
are the mean PHA channels of the two calibration
sources. Note that the nominal calibration source channel of 410 is that
expected at the predicted in-orbit LECS temperature of 
.
Figure 10: PHA channel versus temperature for the two
Fe calibration sources. The dotted lines show the best-fit
linear relations
Spatial gain maps were obtained by computing the gain at
each of the pin-hole locations indicated by
circles in Fig. 7 (click here). The gain of each image pixel was
then estimated by spline interpolation.
Temperature effects were removed by
dividing the data into intervals of constant temperature and using the
average calibration source PHA to normalize the amplitude of each individual
X-ray event according to Eq. (5 (click here)).
The peak PI channel was determined by fitting a model consisting of a
Gaussian profile plus a constant background to the data.
The interpolated gain maps are shown in Fig. 11 (click here)
for Fe 
and for Al 
X-rays.
The region of maximum gain is offset slightly from the center of the FOV,
probably because of the small misalignment between the PMT and gas cell
fundamental. At the edge of the FOV the gain is 
% of the
maximum.
The two gain maps only differ by a scaling factor of 0.238, consistent
with the Al/Fe X-ray energy ratio of 0.232 and the energy discontinuities
at the Xe L edges.
Additional multi pin-hole measurements were taken at the PANTER facility, where other X-ray energies are available. During this campaign, the pin-hole array was stepped in the XY plane, parallel to the focal plane, to increase the spatial sampling. These measurements confirm the smooth surfaces and extend the calibration to lower and higher energies. Again, the spatial gain maps are well behaved, differing only by a scaling factor consistent with the X-ray energy ratios and detector gas edge discontinuities.
Figure 11: Gain maps at 1.49 and 6.41 keV. The crosses indicates the
center of the FOV. The numbers indicate the gain relative to the
average of the calibration sources
Due to the driftless design of the gas cell, X-rays that penetrate
into the cell prior to absorption
give rise to events with lower PI and BL values than events of the
same energy which are detected just beneath the cell entrance window
(see Figs. 9 (click here) and 12 (click here)).
In order to correct the observed PI spectra
for this effect, data obtained at the PANTER facility have been
used to determine the mean PI channel as a function of BL
for incident energies 
. (Below this energy there is
no worthwhile improvement in spectral resolution when this correction
is applied).
For each line a reference PI channel, 
, was determined.
This corresponds approximately to the mean channel of events
absorbed directly beneath the cell entrance window. In order to
determine 
for each line, the function described
in Eq. (8 (click here)) together with a constant background
were fit to the BL spectra and events with BL values
greater than the peak of the distribution selected.
A PI spectrum of these selected events was then accumulated and the
same function fit in order to account for the
remaining small penetration tail. The value of 
is then given by the best-fit value of m.
Thus, for a known
energy, 
, the observed PI spectrum can be corrected for
penetration using:
Here PIC is the corrected channel and 
is the mean PI channel for the observed BL value and
incident energy.
From an examination of the 
distributions
it is apparent that the BL resolution of the
instrument is insufficient to fully correct for
penetration effects in the energy range of interest.
This explains the remaining small exponential tail visible in the corrected
spectrum in the lower panel of Fig. 12 (click here).
During normal astronomical observations there is a further complication
that the actual energy of a detected event, 
, is not
known a priori and only the probability that an event has a certain
incident energy can be estimated. In the LECS data analysis software
a value of 
is assigned to each event taking into account
this probability. The penetration correction can then be
applied using Eq. (6 (click here)). This lack of a priori knowledge of the
incident energy means that e.g. the measured FWHM energy resolution of 9.0%
at Fe 
(6.41 keV) can only be corrected to 8.6% using this
technique, rather than 8.1% if the energy of the incident X-rays is known.
The overall energy gain of the LECS is expected to be linear, with discontinuities at the absorption edges of the detector gas caused by discrete changes in the final ionization state, and hence the amount of energy retained by the Xe atoms across the absorption edges. In order to measure the overall gain, results from the PANTER measurement campaign were utilized since these covered almost the entire energy range of the instrument. The lines used and their energies (Bearden 1967) are given in Table 2 (click here). For each of these lines, the PHA data were first corrected for the overall temperature and position dependence of the gain using Eq. (5 (click here)) and the mean gain map (see Fig. 11 (click here)).
Figure 12: The response of the LECS to monochromatic radiation at
energies of 0.28 keV (upper panel) and 8.06 keV (center panel). The
statistical uncertainties are comparable to the symbol size.
The ``knee'' visible in the 
spectra at channel 
is from Cu 
radiation.
The lower panel shows the effect of performing the penetration correction
described in Sect. 3.3 (click here) on the Cu
spectrum assuming
an incident energy of 8.06 keV
The resulting spectra, 
, can either be represented by a
Gaussian or, at energies 
keV, a Gaussian plus an
exponential low-energy tail.
The upper two panels in Fig. 12 (click here) show observed line profiles
at 0.28 keV, where the mean absorption depth is small, and 8.06 keV, where
it is large (see Fig. 8 (click here)).
The 0.28 keV line profile is well fitted by a Gaussian function,
demonstrating the good low-energy performance of the instrument since the
loss of significant numbers of electrons would result in a
tail towards low energies, which is not evident. The 8.06 keV line
shows an exponential tail extending towards lower energies. This
results from the penetration of X-rays into the gas cell prior to
absorption.
The observed line profiles were modeled using a constant background
together with the following functions:
lines in Table 2 (click here)
where the effects of penetration are not evident:
is the break channel between the two components,
is the e-folding index, m is the peak PI channel of the Gaussian,
is the width of the Gaussian distribution in standard deviations
and 
and 
are the normalizations of the exponential and
Gaussian components, respectively.
Since the two components connect
smoothly at 
, their first derivatives are equal at this point.
(This implies that 
). Some idea of
the quality of fits can be obtained from the upper two panels in
Fig. 12 (click here) where the fitted models are shown as continuous lines.
The penetration correction given in Eq. (6 (click here)) was then
applied to the data from all lines with energies > 2.9 keV
(below this energy the PI and PIC channels are equivalent).
Equations (7 (click here)) or (8 (click here))
were then fit to the PIC spectra, as appropriate, to derive the best-fit
values of m which are used for the PIC to energy conversion. A
linear relation between PIC value and energy was assumed, allowing for a
discontinuity at the Xe 
edge at 4.782 keV.
The result of this fitting gives:
The discontinuity at the Xe L edge is 31 eV. This value is smaller then the 129 eV measured by Bavdaz et al. (1995a) using a prototype detector at BESSY. This difference probably arises because these authors selected only a small fraction of the available data to minimize penetration effects. Such a technique cannot be usefully applied to astronomical measurements. No evidence for a gain discontinuity at the Xe M edge was found in the PANTER data.
The energy resolution of the LECS was determined at each of the energies
listed in Table 2 (click here) using either Eqs. (7 (click here))
or (8 (click here)) and corrected for penetration effects using
Eq. (6 (click here)), as appropriate. No a priori knowledge of the
line energy was assumed, since this will be the case during astronomical
observations. The full width at half-maximum (FWHM) of the PIC energy
resolution, 
, is related to the width of the Gaussian distribution
by 
. The LECS energy
resolution is given by:
and is shown plotted versus energy in Fig. 13 (click here).
The deviation from the expected 
relation has been
previously noted (Simons & de Korte 1989) and explained as
being due to variations in the footprint of the electron cloud
viewed by the PMT.
Figure 13: The LECS penetration corrected energy resolution versus energy.
The best-fit relation given in Eq. (10 (click here)) is shown as a
solid line. The uncertainties are smaller than the symbol size
The coordinate transformation required to translate the
RAWX, RAWY pixel coordinates into absolute position on the focal plane
were obtained using multi pin-hole mask (MP) exposures taken at PANTER.
Due to the finite source distance of
130 m the actual distance between consecutive pinholes projected on
the focal plane is magnified by 
%. This effect is taken into
consideration in the analysis.
The data used for this analysis were obtained using lines of C
(0.28 keV), Al (1.49 keV) and Fe (6.41 keV). For each exposure,
the relation between pixel coordinates and pin-hole
position, as shown in Fig. 14 (click here), was established.
Based on this data, the coordinate transformation required to assign
to each RAWX, RAWY pixel its true
distance along the X and Y axes from the physical center of the
FOV have been determined. A cubic polynomial function has been fit to
the data:
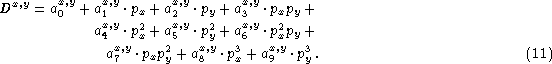
Here, 
is the distance in mm from the physical center of the
FOV (which is located at pixel coordinates RAWX, RAWY = 131.44, 124.12)
along the X and
Y axes, 
, 
and 
are the fitted coefficients
(one set for each axis).
The rms residuals between the data and the fit
along both axes are 
. This corresponds to
about half a pixel and is of the order of the systematics inherent to the
experimental set up. From a comparison of the pin-hole images taken
at different energies, any energy dependence corresponds
to a positional difference of 
, except at the edge of the
FOV where these may be as large as 
.
The positions in mm are converted to linearized pixels by the LECS data
analysis software assuming a pixel size of 8''.
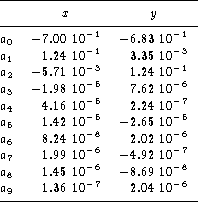
Table 3: Coefficients required to map pixel coordinates into absolute
position on the focal plane
Figure 14: Correspondence between 
, 
pixels (left panel) and
physical space (right panel). Each data point represents the
position of one pinhole
The overall encircled energy function (EEF) of the LECS is a convolution
of those of
the MU and detector modulated by the obscuration of the
entrance window strongback and support grid. Its shape can therefore not be
easily parameterized in a similar manner to that of the MECS (Boella et al.
1996a). Measured, azimuthally averaged, on-axis EEFs are shown in
Fig. 15 (click here).
At low energies the EEF is dominated by
the contribution of the detector, which is approximately
.
This results in
the narrowing of the EEF core visible in Fig. 15 (click here) with increasing
energy. Above 
keV, the broad scattering wings of the mirror response
become important (see Fig. 19 (click here)).
The FWHM of the LECS EEF is given by:
At 6 keV this relation is valid in the central 8' of the FOV. The range
of validity increases with decreasing energy, such that at 0.28 keV it is
valid over the entire FOV.
Figure 15: Measured, azimuthally averaged, on-axis LECS encircled
energy functions at various energies.
Each plot has been offset from the next by 0.1 for clarity. The dotted lines
show the asymptotic values
The effective area of the LECS is primarily limited at low-energies by the transmission of the entrance window and at high-energies by the loss in reflectivity of the MU. The predicted on-axis effective area of the LECS is shown in Fig. 16 (click here). This figure includes the theoretical mirror efficiency (Sacco 1995, private communication), detector absorption efficiency and plasma grid transmission and the measured entrance and plasma protection window transmissions. A constant geometric obscuration due to the window support structure of 17% is assumed. The large change in effective area at 0.28 keV is due to the C K-edge. The effect of the K-edges of N, O, and Al, which are all constituents of the windows, are also visible. The structure between 2-4 keV is caused by the M-edges of the Au mirror material. At the edge of the FOV (i.e. an offset angle of 18'), the effective area of the LECS is 0.4 times that on-axis.
Figure 16: Predicted LECS on-axis effective area
In the PANTER configuration the effective mirror collecting area is reduced to
, including obscuration by the mirror spider (Conti et al. 1994).
The MU effective area was measured at each of the energies listed in
Table 2 (click here) (except that the measurements for the two Ag and
Ti lines were combined, and an additional P (2.01 keV)
measurement was included).
The MU effective area was derived by comparing the count rate
with the MU in place to that during a flat-field exposure (i.e. with
the MU removed).
The derived values were corrected for the effects of strongback and
fine grid obscuration and deadtime and are shown plotted in
Fig. 17 (click here).
This figure also shows the theoretical MU response derived from
ray-tracing simulations of a source at the same distance as that at PANTER.
The agreement between
measurement and theory is good except at low energies (the B and
C measurements at 0.18 and 0.28 keV) where the measured areas are a factor
too high. Such an effect may be related to the
location of the LECS in the PANTER chamber and the complicated behavior
of the MU to off-axis X-rays. In particular, X-rays from within a 
offset angle which are reflected by either one of the first or second
mirror cones only, can reach the focal plane. In addition, for particular
offset angles, X-rays can reach the focal plane without reflection
(Conti et al. 1994).
Thus, it is possible that low-energy X-rays scattered off the
chamber walls during the mirror exposures enter the detector, resulting
in the anomalous area measurements.
An additional effect may be due to molecular contamination of the mirror
surfaces (e.g., Elsner et al. 1994).
However, there is no totally convincing
explanation for this phenomenon and we await the results of in-flight
measurements to verify the low-energy LECS effective area.
Figure 17: Measured and theoretical (solid line) on-axis MU effective area
versus energy in the PANTER configuration
The construction of the strongback and grid are shown in Figs. 4 (click here) and 5 (click here), respectively. The strongback and grid together obscure an average of 17% of normally incident X-rays. However, this obscuration depends on both position in the FOV and X-ray energy in a complex way. The energy dependence arises because:
Figure 18: A scan across the central part of the LECS window
centered on 0.28 keV showing the effects of strongback and fine grid
obscuration.
The distance scale indicates the approximate angular distance from the center
of the FOV
The effect of strongback and fine grid obscuration is illustrated in
Fig. 18 (click here) which shows the LECS counting rate at 0.28 keV
during a 3.9 mm long scan of the central region of the detector
in a direction parallel to the Y axis, using a constant intensity X-ray
beam. The two large (
%)
decreases in count rate delineate the 2.2 mm central strongback square
and are caused by the strongback ribs. A smaller amplitude (
%)
modulation due to the fine grid is also visible. The overall trend
of increasing count rate with distance along the Y axis is probably
due to a small misalignment between the mirror and detector units.
These obscuration effects are treated by means of a Monte-Carlo simulation in the LECS data analysis system. The first stage of this process is a ray-tracing model of the mirror system. This is based on the commercial ray tracing software package, IRT, from Parsec Technology Inc. which has been ``tuned'' to give good agreement with the mirror EEF's obtained at the PANTER facility using the flight MU and the ROSAT Position Sensitive Proportional Counter (PSPC) as a focal plane detector. The spatial resolution of the PSPC is much better than that of the LECS, and is sufficient to allow the intrinsic shape of the MU EEF to be reliably determined. Figure 19 (click here) shows the good agreement between observed MU EEFs and those predicted by the ray-tracing model.
A geometric model of the support structure and the fine grid is then used to determine the fate of an X-ray with given energy and arrival direction. X-rays which exit the MU can reach the entrance window undisturbed, or be absorbed in the fine grid, or interact with the strongback. In the latter case, the photon can be either absorbed or reflected, with a probability that depends on the energy and the angle of incidence with the strongback. Reflected photons may be absorbed by the fine grid. Using the processes described above, it is possible to generate the EEF of the concentrators for any given energy and position in the FOV and to propagate this through the support structure. The effect of this obscuration on the analysis of both extended and variable sources will be evaluated during the Science Verification Phase of the mission.
Figure 19: Azimuthally averaged mirror unit EEFs at two energies
obtained by ray-tracing (squares) and measured using the ROSAT
PSPC at two energies (solid lines). The plots have been offset by
0.5 units for clarity. The dotted lines show the asymptotic values
The primary goal of the LECS is to perform low-energy spectroscopy. Since the low-energy response of the detector is primarily defined by the transmission of the entrance window, a well calibrated window transmission is vital. With this in mind, great care was taken to determine the window transmission paying particular attention to variations near the edges of the constituent materials and to the position dependence of the overall transmission.
Measurements using the available lines at PANTER (Table 2 (click here))
are inadequate for
this purpose, and instead a thorough investigative campaign was performed
at BESSY. The PTB SX-700 plane grating
monochromator beamline was used which
provided energy resolution, 
, of between 5000 at 0.06 keV
to 400 at 1.8 keV, scaling as 
.
Since the entrance window is highly transparent at energies
, measurements were only made in the energy range
0.1 to 1.8 keV.
Transmissions at 500 energy values were measured at five positions in the
central window area. Energy steps
as small as 0.2 eV were used around the absorption edges of the constituents.
These measurements were complemented by a series of measurements in
the center of each of the 8 by 8 fine grid positions in the central 3 by 3
central strongback squares (see Fig. 4 (click here)).
Between 18 and 30 energies were used for these
scans.
The 99% flux width of the beam was 
, smaller than
the fine grid mesh size. This allowed the transmission of the window
to be measured separately from the obscuration caused by the support
structure.
The absolute errors on the transmission are 
% and
the variations in transmission with position < 3%.
A detailed discussion of these measurements is to be found in
Bavdaz et al. (1994, 1995b).
The X-ray cross sections used by Bavdaz et al. (1994) were derived from
tables in
Veigel et al. (1971). Another, more recent, set of coefficients has
been published by Henke et al. (1993). They differ from the
older ones mainly around the absorption edges and are used for the
LECS calibration.
The usual approach to modeling X-ray transmission, T, through an
absorbing layer is to use:
where 
is the density, x the thickness and
the mass absorption coefficient, which for compounds is given
by:
where 
is the mass absorption coefficient of element i and
its fractional weight. By defining 
as the area density
of element i, we can write:
Using the measurements at different energies, gives the area
densities required to describe the X-ray transmission properties of the
window. Unfortunately the chemical state and thickness of the absorber
change the edge absorption characteristics e.g., Bearden & Burr (1967)
and Owens et al.
(1996) and Eq. (14 (click here)) is only a good approximation away from the
edges. As an example, Fig. 20 (click here) shows the actual transmission
around the O K edge compared to the Veigel et al. (1971)
(solid line) and Henke et al. (1993) mass absorption
coefficients (dashed line).
In order to precisely model the LECS window transmission,
the following empirical function has been used:
where the correction factor, 
, is defined as the ratio of the
measured data to that predicted using the
Henke et al. (1993)
coefficients outside the edge regions:
The correction factor is derived from the average of the five high
resolution energy scans and is plotted in Fig. 21 (click here).
As expected, it has a value close to one (i.e. no correction) away from
the edges of constituent materials and above 1.8 keV.
Figure 20: Entrance window transmission around the O K edge.
Predictions using
theVeigel et al. (1971) and theHenke et al. (1993) mass
absorption coefficients are shown as solid and dashed lines,
respectively. The measured data are shown as crosses
Figure 21: The correction factor used to model the transmission of the
entrance window around the absorption edges
The area densities for each of the window constituents were fit at each
position by minimizing the parameter, Q:
where the index ``j'' denotes the energy dependence and ``k'' the window
constituents of H, C, N, O, and Al. Energy regions close to the
absorption edges were excluded.
Table 4 (click here) summarizes
the theoretical composition, based on the design shown in
Fig. 3 (click here).
Figure 22 (click here) shows the measured transmission of the
entrance window and compares it with a 
thick
Be window as used on the ASCA GSPC (Tanaka et al. 1994).
The derived area densities are given in Table {5 (click here).
The fitted curve matches the data well, but is not
superposed for clarity. The complex structure near
the edges is clearly visible.
Figure 22: The measured transmission of the LECS entrance window at one
position. Absorption edges of the constituent
materials are indicated. The theoretical transmission of a
Be window is also shown for comparison
Table 4: Nominal entrance window composition
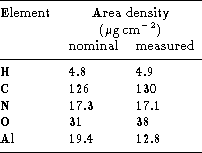
Table 5: Measured entrance window composition
The transmission of the plasma protection window was also measured at BESSY. A high resolution energy scan (500 energy measurements between 0.1 and 1.8 keV) at the center of the window and a high position resolution scan at 3 energies (0.27, 0.90 and 1.55 keV) were performed. The scan revealed < 1% rms spatial variations in transmission. Since this window is located 5 cm above the focal plane, any small transmission variations will be smoothed out and we therefore assume a uniform absorption with position. The absorption of the window has been modeled in a similar manner to that of the entrance window, except that the effect of the support grid is included. The resulting function is plotted in Fig. 23 (click here).
Figure 23: The measured transmission of the plasma protection
window and strongback. Absorption edges of the constituent materials
are indicated
Nearly all incident X-rays with energies in the range 0.1-10 keV that
pass through the entrance window are
absorbed in the 5 cm deep LECS gas cell. The absorption efficiency decreases
slightly at the upper end of the energy range, being 0.996 at 10 keV.
Following photo-electric absorption an
excited ion may relax by the emission of an Auger electron or a
fluorescent photon. The probability that a fluorescent photon
will escape from the detection volume is geometry dependent, and has been
measured for the LECS using data obtained at BESSY and PANTER.
The values given in Table 6 (click here) have
been adopted for use in the LECS calibration and show that 1.68% of
incident X-rays with energies just above the Xe 
edge
produce fluorescent X-rays which are lost from the instrument,
resulting in escape peaks.
This figure is less than the Xe L shell fluorescent
yield of 
% due to the probability that an emitted fluorescent photon
is absorbed within the detector.
Table 6 (click here) gives the escape
fractions for energies between the Xe 
and
Xe 
edges. Above the Xe 
edge the escape fraction
is assumed to decrease linearly with energy, falling to 1.12% at 8.06 keV.
Table 6: LECS escape line data
The VETO and BL signals can be used to minimize the residual background counting rate seen in the LECS. The definition of these signals is given in Sects. 2.2 (click here) and 2.3 (click here). Briefly, the VETO signal is a measure of the fraction of the total light collected by the central anode of the PMT (see Fig. 6 (click here)) and, in general, an on-axis event will have a higher value than an off-axis or extended event. The BL signal is a measure of the duration of scintillation of an event and will, on average, be shorter for events that penetrate into the detector prior to absorption.
Figure 24: BL plotted against VETO at two energies
Figure 24 (click here) shows BL plotted against VETO
for on-axis B (0.18 keV) and Cu
(8.06 keV) events.
Events falling outside the
FOV are excluded. The events with VETO values of 
result from
multiple calibration source events being detected during a single
EU sampling window.
The effects of penetration are clearly seen in the Cu
image,
where a tail towards lower BL and higher VETO
values is evident.
This change in VETO value is caused by the increased PMT viewing angle
of penetrating events which are absorbed closer to the central
anode (see Fig. 6 (click here) and Eq. (4 (click here))). At 0.18 keV,
because of low signal strength, the BL signal distribution
is significantly broadened by the EU circuitry. In addition, at low
energies there
is an unexpectantly large number of events with high BL values.
The magnitude of this effect appears to be inversely correlated with mean
absorption depth.
It is possible that these events are absorbed
very close to the entrance window where the electric field is non-uniform
due to the undulating window surface. Figure 25 (click here) shows an
optical image of part of an entrance window foil and illustrates
the irregular nature of the foil in each of the 250 by 
squares
which correspond to the gridlets of the window support grid
(see Fig. 5 (click here)).
Figure 25: An optical image of part of an entrance window foil showing
the irregular nature of the foil in each of 250 by 
gridlets. The lightly colored thin lines show the location
of part of the window support grid. Part of a strongback rib
is located over the thicker line
Figure 26: The allowed BL range for 90% X-ray acceptance efficiency
shown as a hatched region
Figure 26 (click here) shows the allowed range of BL plotted
against PI energy channel for a 90% X-ray acceptance as a hatched area.
The broadening of the BL distribution at low-energies
discussed above is visible, as is the effect of change in
mean absorption depth around the Xe L edge at a PI channel of 
.
This figure has been obtained using PANTER data for the lines shown
in Table 2 (click here) (except that the results for the
Ag 
and 
and Ti
and 
lines have been combined)
and by making a series of ``box cuts'' centered
on the calibration energies.
The LECS background counting rate within the FOV has been estimated using a
exposure taken in SSD's X-ray beam.
A VETO acceptance interval of 30 to 65 combined with BL cuts
of the type described above were applied to the data to give count rates
of 
for 90%
X-ray acceptance and
for 99%
X-ray acceptance.
(Note that the 
in the count rate units refers to the window area).
Figure 27 (click here) shows the effect of these selections.
The increase in counts observed in the incident spectrum around PI channel
600 is primarily due to event pile up from the calibration sources. As
Fig. 27 (click here) illustrates, these events are efficiently removed
by the VETO selection. At the lowest PI channels there
is an increase in detected event rate which is probably due to electronic
noise. The EU analog thresholds were modified following the
PANTER calibration and this effect is not expected to occur in space.
Figure 27: The effect of VETO and BL selection on the laboratory background
spectrum within the FOV. The observed spectrum is shown as a
dashed histogram and the spectrum remaining following selection as a
solid histogram. 1
uncertainties are indicated.
The count rate scale is given by the right ordinate.
The efficacy of each of the selection techniques is given by the
left ordinate. See the text for a description of the spectra