The results of the present calculations include the following sets of data: (a) energies of computed LS bound states of Fe I, (b) dipole oscillator strengths among all LS multiplets, and (c) total photoionization cross sections of the LS bound states, and partial cross sections for photoionization into specific states of Fe II (the ground state and several other excited states).
As the first step energies for bound state terms of Fe I are obtained,
and
a total of 1 117 states in LS coupling were found up to 
.
Table 4 compares a small sample of the computed energy levels
separately for septets,
quintets, triplets, and singlets with
experimental values from Nave et al. (1994).
The agreement for septets is good even for highly excited multiplets.
the overall error of calculated energies with respect to observed values,
weighted over the energy of the
multiplet
(
),
is about 1.9%.
The agreement for quintet states can be
regarded as satisfactory, particularly for terms with absolute energies
greater than 0.2 Ry. It is noticed that the calculated energy for
the 
ground state of Fe I agrees with the observed energy
to about 1.2%, and the averaged difference between calculated and
observed energies weighted over the multiplet energies is about 4.4%.
As expected,
the results for the calculated energies of the triplets and singlets present
the largest discrepancy with experiment. The overall difference
with observed energies for triplets is
about 8.9%. Calculated energies for singlet are in reasonable agreement
with experiment for terms with absolute energy greater than 0.2 Ry;
however, greater discrepancies are observed for higher excitation terms
and the averaged difference with experiment is about 10.6%.
Dipole oscillator strengths (f-values) for 32 316 transitions among the calculated states of Fe I were obtained in LS coupling. This set includes transitions when the lower state lies below the first ionization threshold and the upper state lies above. These transitions are important because they might contribute to the total photo-absorption, but do not appear as resonances in the photoionization cross sections.
There are two criteria commonly used in assessment of the accuracy
of oscillator strengths. First, both length and velocity forms of
the oscillator strengths are calculated and compared with each other.
This provides a check on the accuracy of the wavefunctions and,
therefore, on the accuracy of the f-values (Berrington et al. 1987).
Figure 1 (click here) shows the log of the absolute value of the velocity form of
the gf-values, plotted against the log of the length form of the
gf-values separately for septets, quintets, triplets, and singlets. In
each panel the statistical dispersion of the plot for 
is indicated. It is observed that dispersion in the gf-values for each
symmetry is consistent with the differences found between the calculated
energies and the experimental ones. Septets, whose calculated energies
agree well with experiment, exhibit the lowest
dispersion in the gf-values of only 11%. Transitions among quintet terms
have a greater dispersion of about 20%. Triplets present the largest
dispersion (
) consistently with the discrepancies found
for the energy levels; however, for transitions with
the dispersion is about 22%.
The dispersion for transitions among
singlet states is about 27%.
The second accuracy evaluation is the comparison of a limited number
of individual gf values with those observed experimentally by
Nave et al. (1994), and those in the critical compilation of
transition probabilities by Fuhr et al. (1988). For this comparison,
presented in Table 4, the fine
structure gf values presented by Nave et al. and Fuhr et al. were
summed, though for some multiplets the experimental data is
incomplete. Some improvement to the accuracy of the calculated gf values
can be obtained by correcting the calculated energy difference for the
transitions with experimental energies, i.e.
where 
and 
are the corrected and
calculated gf-values respectively and 
and
are the experimental and calculated energy differences
between the levels.
Table 4: Comparison of calculated (cal) energy levels in Ry with
the observed (obs) levels from Nave et al. (1994)
Table 5: Comparison of calculated and corrected gf-values
with experimental measurements from Nave et al. (1994) and
Fuhr et al. (1988)
Figure 1: log 
plotted against log 
for transitions
between calculated LS terms
Table 5 shows some significant differences
with the two sources of experimental data. In most cases these differences
arise from incompleteness of the set of fine structure f-values, measured
within an LS multiplet, in
the earlier compilation by Fuhr et al. (1988) as compared to the more
complete work by Nave et al. (1994). In some other cases,
however, differences up to 40% come from the
experimental measurements themselves. It is also noted that the effect
of correcting the calculated gf-values using experimental energy differences
is quite significant, and in most cases seems to bring the gf-values closer
to those measured experimentally. Unfortunately, it is difficult to
derive conclusions regarding the accuracy of the gf-values
for transitions among septets since there
seems to be no complete experimental data for any multiplets. Thus the
values given in Table 5, summed over the available fine structure
components, should be considered as lower limits to the total LS
multiplet strength.
Oscillator strengths for quintets compare reasonably well with experiment,
the differences being within 
with only two exceptions.
Once again, triplets and singlets present the largest discrepancies
with respect to observed values, though most values are in good
agreement, 
, with experiment.
The dispersion between length and velocity forms of the oscillator strengths
and the comparison of a sample of values with experimental measurements
suggests
that for septets and quintets the present gf may be accurate to the
, gf-values for singlets to about 30%,
and for triplets to about
. The present gf-values could be
considerably improved if corrected using experimental energy separations;
this is recommended for practical applications.
The importance of including ionization of the inner 3d shell in the
calculation of photoionization cross sections of Fe I
was investigated in a previous paper (Bautista
& Pradhan 1995). Figures 1a and 1b of this paper show that
when the inner-shell ionization channels into 
and 
terms of Fe II are included in the CC expansion, both the background and the
resonance structures of the photoionization cross
sections of Fe I are considerably enhanced. Moreover, the CC
result including coupling to the 3d subshell differs by more than three
orders of magnitude in the energy region below about 1 Ry from earlier
results by Reilman & Manson (1979) using the central field
approximation and Verner et al. (1993) in the Dirac-Hartree-Slater
approximation. This is because both of these approximations
neglect the complex correlation effects,
such as the coupling to inner-shell channels, that give rise to an unphysical
discontinuous jump of several orders of magnitude. For
energies of the ionizing photon greater than 1 Ry our results agree
well with these earlier results.
Figure 2 (click here) compares the present ground state cross section with that
from Kelly & Ron
(1972) and Kelly (1972).
The first of these papers concerns the
small range of energy from the ionization threshold to 10 eV (
), and the second paper deals with the cross section for a more extended
range of energies.
The agreement
between the present work and both of these cross sections
is remarkably good below 0.73 Ry, where the cross
section is dominated by correlations involving the terms of the core ion
, 
, 
, and 
.
Beyond this energy Kelly's calculations
underestimate the actual cross section; most likely due to missing
correlations from the 
, 
and 
terms. Nevertheless, Kelly
included contributions from 
that produce a sharp jump of the
cross section near 0.79 Ry. An interesting feature in Kelly's cross section is
the series of resonances due to 
autoionizing
states (see Fig. 7 of Kelly & Ron 1972). The position of the
strongest set of these resonances obtained by Kelly was about 0.89 Ry while the
actual structure of the peak and its hight were rather uncertain. The present
calculations reproduce such a feature but at 0.94 Ry and it is considerably
higher than in Kelly's results. Some other
resonances of this series found by Kelly are also seen in the present
cross section. Another important characteristic of the cross section is its
sharp jump at the position of the thresholds for ionization of the
inner 3d subshell. Kelly's calculations give a single edge at 1.16 Ry
for all the contributions due to 
and 
.
In the present calculation separate edges are obtained for each of these
thresholds, as well as for those of 
and 
which were not
considered by Kelly. Finally, Kelly's cross section at high energies
(above the thresholds associated with 3d inner-shell ionization)
agrees well with
both the present results and those from central field type approximations
(Reilman & Manson 1979; Verner et al. 1993).
Figure 2: Photoionization cross section (
(Mb))
of the ground state 
of Fe I as a function of
photon energy in Ry: full curve, present result; broken curve, Kelly (1972).
Thresholds from all electronic configurations included in present computation
are marked
Photoionization cross sections were calculated for all computed bound states
with energy below the first ionization potential of Fe I.
In order to delineate in detail the autoionization resonances
near the ionization thresholds a very fine mesh of energies,
typically about 2000 points, was used in the range of up to 0.3 Rydberg
above the threshold.
Figure 3 (click here) shows the
photoionization cross section of the two lowest excited terms of Fe I
and 
.
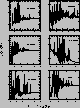
Figure 3: Photoionization cross sections (
(Mb)) as a function of
photon energy in Ry for a sample of excited states of Fe I
In practical applications, particularly non-LTE spectral models, it is important to determine accurately the level population in the excited levels of the residual ion following photoionization. Therefore, partial cross sections for photoionization of the ground state of Fe I into the ground and excited terms of Fe II have been calculated. A few examples of these partial cross sections were given in an earlier paper (Bautista & Pradhan 1995). Also in that paper, we show examples of the so called photoexcitation-of-core (PEC) resonances in photoionization cross sections along Rydberg series of Fe I. Such PEC resonances result from strong dipole couplings between opposite parity terms within the target ion (Yu & Seaton 1987). The present work entails the full set of calculations for all 1 117 bound states, including partial cross sections into the ground and excited states with multiplicity (2L+1) = 5 and 7 of Fe II.
