According to the core aperture photometry technique (Bushouse 1993), the HST instrumental magnitudes are usually defined as
where F is the total number of counts within the aperture radius, B is
the background value within a suitably chosen annulus centered on each
star peak, 
is the aperture area, t is
the exposure time, 
is the fraction of energy falling
into the core aperture with respect to that in the annulus, and
is the
inverse sensitivity of the instrument
mode used (detector + filters), and finally
stands for the pass-band under consideration.
The quantity
is the flux of photons per unit time
measured by the instrument.
To derive the theoretical counterpart of the above magnitudes,
first we calculate
from spectral energy distribution of given 
's
gravities (
) and chemical
composition the quantity
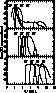
Figure 1: The functions 
for the indicated pass-bands of the WFPC2
(see the text for more details)
The wavelength 
is in Å. Each 
is normalized to
its peak value. The top Panel shows the filters
F170W (solid), F218W (dotted), F255W (dashed), and F300W (long-dashed). The
middle panel is for F336W (solid), F439W (dotted), F450W (dashed), F555W
(long-dashed). The bottom panel is for F606W (solid), F702W (dotted), F814W
(dashed) and F850LP (long-dashed)
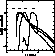
Figure 2: The functions 
for the indicated pass-bands of the FOC
(see the text for more details).
The wavelength 
is in Å. Each 
is normalized to
its peak value. The filters are F150W+F130LP (long dashed), F175W
(dotted-dashed), F220W (dotted), and F342W (dashed)
where 
is the spectral energy distribution of the source,
is the product of the filter
transmission 
and the response function 
of the telescope assembly and detector in
use, and all other symbols have their usual meaning (h is the
Planck constant and c is the speed of light).
According to its definition,
is the number of photon emitted per unit of time
by an idealsource with 
and detected by the
filter in use. This quantity is then scaled to that received by a collector of
unit area when the source is located at the distance of 10 pc.
Finally, large grids of 
are computed at varying
, gravity, and chemical composition.
Figure 3: WFPC2: the colours 
, 
,
, 
and
versus 
for the solar composition
[Y=0.28, Z=0.020]
and 
Figure 4: WFPC2: the colours 
, 
,
,
and 
versus 
for the solar composition
[Y=0.28, Z=0.020] and log g=5
Figure 5: WFPC2: the colours 
, 
,
, 
, and
versus 
for the solar composition
[Y=0.28, Z=0.020] and log g=5
Figure 6: WFPC2: the colours 
,
,
, 
, 
, and
versus 
for the solar composition [Y=0.28, Z=0.020]
and log g=5
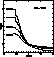
Figure 7: WFPC2: the colours 
, 
,
, and 
versus 
for the solar composition [Y=0.28, Z=0.020]
and log g=5
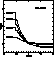
Figure 8: WFPC2: the colours 
, 
,
, and 
versus 
for the solar composition [Y=0.28, Z=0.020]
and log g=5
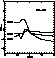
Figure 9: FOC: the colours
, 
and 
versus 
for the solar composition [Y=0.28, Z=0.020]
and log g=5
Figure 10: FOC: the colours
, 
and 
versus 
for the solar composition [Y=0.28, Z=0.020]
and log g=5
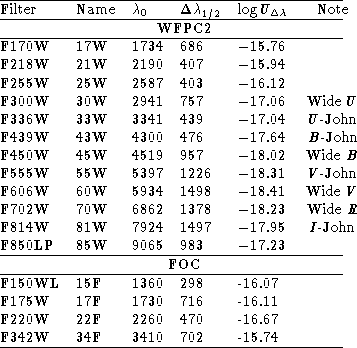
Table 1: Main characteristics of the filters in use. All wavelengths are
in Å
Second, we calculate the Bolometric Corrections defined as
where 
is the area of the collecting surface, and 
is
the absolute bolometric magnitude of the Sun, for which we adopt 4.72.
The
are
functions of the 
, gravity, and chemical composition.
Finally,
the real absolute magnitude 
of a star of any luminosity,
, gravity, and chemical composition is given by
The apparent magnitudes follow from taking into account distance modulus and extinction.
The optical characteristics of the filters in use are given in the
WFPC2 and FOC Instrumental Handbooks and do not need to be
presented here. Suffice it to recall the main characteristics defining each
filter, i.e. the peak wavelength 
and the half-peak width
together with the
inverse sensitivity 
of the instrument
mode used (detector + filters). These parameters are summarized in
Table 1 (click here).
The constants 
for the WFPC2 pass-bands are
derived from the calibrated WFPC2 synthetic photometric system
of Holtzman et al. (1995a,b)
where the zero points refer
to Vega. These constants are calculated for the gain
factor 14e
/DN and aperture radius of 0.5''. Wherever possible the
correction to the aperture of 3'' has been applied using the data
contained in Table 5B of
Holtzman et al. (1995a,b) for the WF3. This has been feasible for the
pass-bands 17W, 21W, 25W, 30W, 33W, 43W, 45W, 55W and 81W.
The magnitudes for the remaining pass-bands (45W, 60W, 70W, and 85W)
refer to the aperture of 0.5'' radius.
In the case of the FOC pass-bands, the constants
are taken directly from the Instrumental Handbook.
The functions
for the WFCP2
are shown in Fig. 1 (click here)
whereas those for the FOC are given in Fig. 2 (click here).
The functions 
s are displayed in
Figs. 1 (click here) and 2 (click here) normalized to
their peak value. Notice in Fig. 1 (click here) that all the filters short-ward of
45W have long tails toward the visible/red wavelength region, some of
them showing secondary peaks. This anomalous behavior of the filters will
immediately reflect into a non monotonic behavior of the colours (see below).
Figure 11: Left Panel: three isochrones in the CMD for the
WFPC pass-bands 17W and 21W. Dashed line, solid line and dotted line
are for the 10 Gyr, 1 Gyr and 0.01 Gyr ages, respectively.
Right Panel: the same but for the pass-bands 25W and 30W
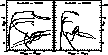
Figure 12: Left Panel: three isochrones in the CMD for the
WFPC pass-bands 33W and 43W. Dashed line, solid line and dotted
are for the 10 Gyr, 1 Gyr and 0.01 Gyr ages, respectively.
Right Panel: the same but for the pass-bands 45W and 55W
Figure 13: Left Panel: three isochrones in the CMD for the
WFPC pass-bands 60W and 70W. Dashed line, solid line and dotted line
are for the 10 Gyr, 1 Gyr and 0.01 Gyr ages, respectively.
Right Panel: the same but for the pass-bands 81W and 85W
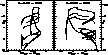
Figure 14: Left Panel: three isochrones in the CMD for the
FOC pass-bands 15F and 17F. Dashed line, solid line and dotted
line are for the 10 Gyr, 1 Gyr and 0.01 Gyr ages, respectively.
Right Panel: the same but for the pass-bands 22F and 34F
Figure 15: Integrated colours as function of the age for the SSP with solar
composition [Y=0.28, Z=0.02] and the Salpeter initial mass function
Figure 16: Integrated colours as function of the age for the SSP with solar
composition [Y=0.28, Z=0.02] and the Salpeter initial mass function. Left Panel:
(dotted), 
(dashed), and
(solid). For each
colour the lower curve refers to Z=0.0004, the upper curve to Z=0.02.
Right panel: two colour plane 
versus 
The library of stellar spectra in use is the one
developed by Bressan et al. (1994) and
Tantalo et al. (1996). The main body of the spectral library is from
Kurucz (1992)
however extended in the high and low temperatures ranges.
For 
K pure black-body spectra is assigned.
For 
K, the new catalog of stellar fluxes
by Fluks et al. (1994) together with their scale of
is adopted.
All other details can be found in the studies quoted above.
