As a basis for our database we have taken the flux density
measurements published by Lorimer et al. (1995). These
observations were made between July 1988 and October 1992 using the
76-m Lovell radio telescope at Jodrell Bank, at frequencies 408, 606,
925, 1408 and 1606 MHz. Lorimer et al. (1995) excluded from
their sample those pulsars which were too weak to obtain reliable flux
density measurements as well as the millisecond pulsars. We have
extended this database by observations made at higher frequencies by
different authors mentioned earlier or those unpublished but made
available at MPIfR archives in Bonn. All observations at frequency
range from 1.4 GHz to 43 GHz were made with the 100-m radio telescope
of the MPIfR at Effelsberg and are available in European Pulsar
Network Database (Lorimer et al. 1998). Some values at 1.4
and 1.6 GHz were also published by Lorimer et al. (1995). We
performed additional observations at 4.85 GHz of 43 very weak pulsars
in August 1998. We managed to detect 30 objects and those undetected
are listed in Table 1. The detection limit of
![]() mJy for
the survey published by Kijak et al. (1998) is clearly visible
from this table. The observations published by Izvekova et
al. (1981) and Malofeev et al. (2000) were
performed at the Pushchino Radio Astronomical Observatory of the
Lebedev Physical Institute.
mJy for
the survey published by Kijak et al. (1998) is clearly visible
from this table. The observations published by Izvekova et
al. (1981) and Malofeev et al. (2000) were
performed at the Pushchino Radio Astronomical Observatory of the
Lebedev Physical Institute.
| PSR B | Time |
|
PSR B | Time |
|
| [min] | [mJy] | [min] | [mJy] | ||
| 0621-04 | 30 | 0.02 | 1820-14 | 20 | 0.02 |
| 1246+22 | 50 | 0.01 | 1834-04 | 30 | 0.01 |
| 1534+12 | 20 | 0.01 | 1839-04 | 25 | 0.03 |
| 1600-27 | 25 | 0.01 | 1848+12 | 20 | 0.01 |
| 1811+40 | 20 | 0.01 | 2210+29 | 100 | 0.01 |
| 1813-17 | 25 | 0.01 | 2323+63 | 20 | 0.03 |
In order to calibrate the flux density of a pulsar using a system in
the Effelsberg Radio-observatory, a noise diode installed in every
receiver is switched synchronously with the pulse period. The energy
output for the noise diode is then compared with energy received from
the pulsar, since the first samples of an observed pulse profile
contain the calibration signal while the remaining samples contain the
pulse. The energy of the noise diode itself can be calibrated by
comparing its output to the flux density of a known continuum
sources. This pointing procedure is generally performed on well known
reliable flux calibrators, e.g. 3C 123, 3C 48, etc. From these pointing
observations a factor
![]() translating the height of the
calibration signal into flux units, is derived. The energy of a pulse
is given as the integral beneath its waveform which in arbitrary units
yields
translating the height of the
calibration signal into flux units, is derived. The energy of a pulse
is given as the integral beneath its waveform which in arbitrary units
yields
 |
(1) |
 |
(2) |
 |
(3) |
 |
(4) |
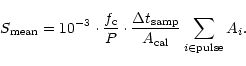 |
(5) |
Pulsars are generally known to be stable radio sources although the measured flux density varies due to diffractive and refractive scintillation effects (e.g. Stinebring & Condon 1990). Interstellar scintillations are caused by irregularities in the electron density of the interstellar medium. The observed flux variations are frequency and distance dependent and also depend on the observing set-up, i.e. on the relative width of observing and scintillation bandwidth (e.g. Malofeev et al. 1996; Malofeev 1996). Unless the receiver bandwidth is significantly larger than the scintillation bandwidth, which increases with frequency, strong variations in the observed flux densities are to be expected. Usually, however, the amplitude of scintillation decreases towards higher frequencies, so that those data are less influenced by the scintillation effects. Nevertheless, the question of intrinsic variations on very short and very long time scales remains still open (cf. Stinebring & Condon 1990). Assessing the situation is hampered by the fact that many authors do not estimate the always present influence of interstellar scintillations or do not quote error estimates at all. Given the difference in the observing set-ups for given observatories, a careful analysis is difficult. We try to circumvent this unpleasant situation by estimating errors for the pulsar flux densities in our sample from published values, wherever available, and standard deviations of the average of single measurements. If only one measurement was available, an error estimate could not be computed although it may happen that form of the spectrum changes when new measurements are added.
Since a robust theory of pulsar radio emission does not exist, the
true shape of pulsar spectra is still not known. A fair first attempt
is to model them by simple power laws. Previous studies (e.g. Sieber
1973; Malofeev et al. 1994) showed however
that some pulsar spectra cannot apparently be described by this
simple approach. Usually, such a conclusion is reached after a visual
inspection of the data, i.e. after a power law fit has been
done. However, if pulsar spectra are indeed more complicated, the
usual next step to fit a composite (or "broken'') power law is just
another approximation, where the undersampling of the spectrum in the
observed range of frequencies would place any fitted "break'' naturally
in the range of a few GHz, i.e. the range where they are indeed
usually observed as it was clearly pointed out by Thorsett
(1991). Nevertheless, even if two power laws are just
another approximation to a "true'' spectrum, any need to fit a break in
order to describe the data adequately would represent a valuable hint
on the true nature of pulsar spectra. It is therefore very important
to search for such breaks in the spectra, while keeping just discussed limitations
in mind. We believe, however, that one has
to be more quantitative when describing the need for fitting a two power laws
rather than a simple power law. This is even more important in the
light of the latest results on millisecond pulsar spectra (Kramer
et al. 1999; Kuzmin & Losovski 2000), where no significant
break (not even a low frequency turn-over) has been found. Hence, we
adopted in this work the following approach: firstly, we fitted a
simple power law to the flux density data, assuming that this
describes the data sufficiently. We calculated a ![]() and the
probability Q that a random
and the
probability Q that a random ![]() exceeds this value for a given
number of degrees of freedom. These computed probabilities give a
quantitative measure for the goodness-of-fit of the model. If Q is
very small then the apparent discrepancies are unlikely to be chance
fluctuations. Much more probably either the model is wrong, or the
measurement errors are larger than stated, or measurement errors might
not be normally distributed. Generally, one may accept models with
exceeds this value for a given
number of degrees of freedom. These computed probabilities give a
quantitative measure for the goodness-of-fit of the model. If Q is
very small then the apparent discrepancies are unlikely to be chance
fluctuations. Much more probably either the model is wrong, or the
measurement errors are larger than stated, or measurement errors might
not be normally distributed. Generally, one may accept models with ![]() 0.001 (Press et al. 1996). Secondly, we assumed that
a two power law had to be fitted to the data, using the following
rules:
0.001 (Press et al. 1996). Secondly, we assumed that
a two power law had to be fitted to the data, using the following
rules:
 |
(6) |
| PSR B | Freq. range |
|
Q | PSR B | Freq. range |
|
Q | |||
| [GHz] | ||||||||||
| 0011+47 | 0.4 - 4.9 | -1.3 | 0.10 | 8.3E-01 | 0950+08 | 0.4 - 10.6 | -2.2 | 0.03 | 1.7E-02 | |
| 0031-07 | 0.4 - 10.7 | -1.4 | 0.11 | 4.1E-03 | 1010-23 | 0.4 - 0.6 | -1.9 | |||
| 0037+56 | 0.4 - 4.8 | -1.8 | 0.05 | 6.3E-03 | 1016-16 | 0.4 - 1.4 | -1.7 | 0.28 | 9.1E-01 | |
| 0045+33 | 0.4 - 1.4 | -2.5 | 0.26 | 1039-19 | 0.4 - 1.4 | -1.5 | 0.28 | 6.8E-01 | ||
| 0052+51 | 0.4 - 1.4 | -0.7 | 0.14 | 6.1E-01 | 1112+50 | 0.4 - 4.9 | -1.7 | 0.11 | 6.0E-02 | |
| 0053+47 | 0.4 - 4.9 | -1.6 | 0.09 | 1133+16 | 0.4 - 32.0 | -1.9 | 0.06 | 7.4E-02 | ||
| 0059+65 | 0.4 - 1.6 | -1.6 | 0.13 | 1.4E-01 | 1254-10 | 0.4 - 1.6 | -1.8 | 0.16 | 6.4E-01 | |
| 0105+65 | 1.4 - 1.4 | -1.9 | 0.19 | 4.3E-01 | 1309-12 | 0.4 - 1.4 | -1.7 | 0.16 | 2.8E-01 | |
| 0105+68 | 0.4 - 1.4 | -1.8 | 0.22 | 1322+83 | 0.4 - 1.4 | -1.6 | 0.30 | 8.7E-01 | ||
| 0114+58 | 0.4 - 1.4 | -2.5 | 0.21 | 8.5E-01 | 1508+55 | 0.4 - 4.9 | -2.2 | 0.07 | 5.2E-02 | |
| 0138+59 | 0.4 - 1.4 | -1.9 | 0.16 | 7.0E-01 | 1530+27 | 0.4 - 4.9 | -1.4 | 0.10 | 1.3E-01 | |
| 0144+59 | 0.4 - 14.6 | -1.0 | 0.04 | 6.1E-04 | 1540-06 | 0.4 - 4.9 | -2.0 | 0.11 | 4.0E-02 | |
| 0148-06 | 0.4 - 1.4 | -2.7 | 0.58 | 4.6E-01 | 1541+09 | 0.4 - 4.9 | -2.6 | 0.04 | 2.7E-03 | |
| 0149-16 | 0.4 - 1.4 | -2.1 | 0.26 | 2.3E-01 | 1552-23 | 0.4 - 4.9 | -1.8 | 0.08 | 1.1E-02 | |
| 0153+39 | 0.4 - 0.6 | -2.2 | 1552-31 | 0.4 - 1.4 | -1.6 | 0.19 | 3.0E-04 | |||
| 0154+61 | 0.4 - 1.4 | -0.9 | 0.12 | 1.4E-03 | 1600-27 | 0.4 - 1.4 | -1.7 | 0.13 | 4.0E-04 | |
| 0320+39 | 0.4 - 1.4 | -2.9 | 0.24 | 5.2E-01 | 1604-00 | 0.4 - 4.9 | -1.5 | 0.08 | 6.8E-01 | |
| 0329+54 | 1.4 - 23.0 | -2.2 | 0.03 | 7.5E-04 | 1607-13 | 0.4 - 0.6 | -2.1 | 0.45 | ||
| 0331+45 | 0.4 - 1.4 | -1.9 | 0.24 | 1.5E-01 | 1612+07 | 0.4 - 1.4 | -2.6 | 0.30 | 1.7E-01 | |
| 0339+53 | 0.4 - 1.4 | -2.2 | 0.28 | 2.5E-02 | 1612-29 | 0.4 - 0.6 | -0.8 | 0.98 | ||
| 0353+52 | 0.4 - 1.4 | -1.6 | 0.12 | 7.4E-01 | 1620-09 | 0.4 - 4.9 | -1.7 | 0.13 | 1.5E-01 | |
| 0402+61 | 0.4 - 1.4 | -1.4 | 0.08 | 1.4E-01 | 1633+24 | 0.4 - 1.4 | -2.4 | 0.31 | ||
| 0410+69 | 0.4 - 1.4 | -2.4 | 0.13 | 8.1E-04 | 1642-03 | 0.4 - 10.6 | -2.3 | 0.05 | 6.7E-01 | |
| 0447-12 | 0.4 - 1.4 | -2.0 | 0.11 | 1.4E-02 | 1648-17 | 0.4 - 1.4 | -2.5 | 0.26 | 5.9E-02 | |
| 0450+55 | 0.4 - 4.9 | -1.5 | 0.04 | 6.0E-02 | 1649-23 | 0.4 - 1.4 | -1.7 | 0.09 | 5.6E-01 | |
| 0450-18 | 0.4 - 4.9 | -2.0 | 0.05 | 2.9E-08 | 1657-13 | 0.4 - 0.6 | -1.7 | 0.36 | ||
| 0458+46 | 0.4 - 1.4 | -1.3 | 0.05 | 1.2E-05 | 1700-18 | 0.4 - 1.4 | -1.9 | 0.23 | 4.8E-05 | |
| 0523+11 | 0.4 - 1.4 | -2.0 | 0.06 | 1.4E-01 | 1700-32 | 0.4 - 0.6 | -3.1 | 0.27 | ||
| 0525+21 | 0.4 - 4.9 | -1.5 | 0.12 | 4.4E-01 | 1702-19 | 0.4 - 4.9 | -1.3 | 0.05 | 5.3E-01 | |
| 0531+21 | 0.4 - 1.4 | -3.1 | 0.18 | 5.7E-01 | 1706-16 | 0.4 - 32.0 | -1.5 | 0.04 | 1.1E-01 | |
| J0538+2817 | 1.4 - 4.9 | -1.2 | 0.57 | 1709-15 | 0.4 - 4.9 | -1.7 | 0.06 | 8.7E-01 | ||
| 0559-05 | 0.4 - 4.9 | -1.7 | 0.04 | 7.6E-01 | 1714-34 | 0.4 - 1.4 | -2.6 | 0.34 | ||
| 0609+37 | 0.4 - 1.4 | -1.5 | 0.25 | 3.5E-01 | 1717-16 | 0.4 - 4.9 | -2.2 | 0.05 | 5.7E-01 | |
| 0611+22 | 0.4 - 2.7 | -2.1 | 0.04 | 8.5E-01 | 1717-29 | 0.4 - 1.4 | -2.2 | 0.20 | 8.8E-01 | |
| 0621-04 | 0.4 - 1.4 | -0.4 | 0.29 | 5.0E-01 | 1718-02 | 0.4 - 1.4 | -2.2 | 0.16 | 1.6E-06 | |
| 0626+24 | 0.4 - 4.9 | -1.6 | 0.08 | 1.2E-03 | 1718-32 | 0.4 - 1.4 | -2.3 | 0.06 | 3.9E-01 | |
| 0628-28 | 0.4 - 10.6 | -1.9 | 0.10 | 6.8E-01 | 1726-00 | 0.4 - 0.6 | -2.3 | 0.47 | ||
| 0643+80 | 0.4 - 4.9 | -1.9 | 0.08 | 2.3E-01 | 1727-33 | 0.4 - 1.4 | -1.3 | |||
| 0655+64 | 0.4 - 1.4 | -2.1 | 0.30 | 1.0E-01 | 1730-22 | 0.4 - 1.4 | -2.0 | 0.15 | 1.4E-01 | |
| 0656+14 | 0.4 - 1.4 | -0.5 | 0.17 | 1.3E-01 | 1732-07 | 0.4 - 1.4 | -1.9 | 0.12 | 1.4E-09 | |
| 0727-18 | 0.4 - 1.4 | -1.6 | 0.11 | 1.3E-02 | 1734-35 | 0.6 - 1.4 | -1.6 | 0.30 | ||
| 0740-28 | 0.4 - 10.6 | -2.0 | 0.03 | 1.1E-07 | 1735-32 | 0.4 - 1.6 | -0.9 | 0.12 | 2.1E-02 | |
| 0751+32 | 0.4 - 4.9 | -1.5 | 0.07 | 1.8E-01 | 1736-31 | 0.6 - 1.6 | -0.9 | 0.20 | 4.2E-01 | |
| 0756-15 | 0.4 - 4.9 | -1.6 | 0.13 | 6.0E-04 | 1737+13 | 0.4 - 4.9 | -1.5 | 0.10 | 2.8E-01 | |
| 0809+74 | 0.4 - 10.6 | -1.4 | 0.06 | 6.7E-02 | 1737-30 | 0.4 - 1.4 | -1.3 | 0.10 | 4.5E-01 | |
| 0818-13 | 0.4 - 4.9 | -2.3 | 0.05 | 3.4E-01 | 1738-08 | 0.4 - 4.9 | -2.2 | 0.08 | 6.9E-02 | |
| 0820+02 | 0.4 - 4.9 | -2.4 | 0.08 | 9.5E-01 | 1740-03 | 0.4 - 1.4 | -1.5 | |||
| 0834+06 | 0.4 - 4.9 | -2.7 | 0.11 | 2.1E-02 | 1740-13 | 0.4 - 1.4 | -2.0 | 0.19 | 2.3E-02 | |
| 0853-33 | 0.4 - 1.4 | -2.4 | 0.20 | 5.4E-01 | 1740-31 | 0.6 - 1.4 | -1.9 | 0.11 | ||
| 0906-17 | 0.4 - 1.4 | -1.4 | 0.16 | 2.0E-01 | 1742-30 | 0.4 - 4.9 | -1.6 | 0.04 | 1.5E-06 | |
| 0917+63 | 0.4 - 1.4 | -1.7 | 0.37 | 1745-12 | 0.4 - 1.4 | -2.1 | 0.12 | 3.4E-03 | ||
| 0919+06 | 0.4 - 10.6 | -1.8 | 0.05 | 7.6E-01 | 1746-30 | 0.4 - 1.4 | -1.5 | 0.39 | ||
| 0940+16 | 0.4 - 1.4 | -1.3 | 0.30 | 5.3E-01 | 1747-31 | 0.6 - 1.4 | -1.2 | 0.31 | ||
| 0942-13 | 0.4 - 1.4 | -3.0 | 0.30 | 8.8E-01 | 1750-24 | 0.9 - 4.9 | -1.0 | 0.07 | 1.1E-06 | |
| 0943+10 | 0.4 - 0.6 | -3.7 | 0.36 | 1753+52 | 0.4 - 4.9 | -1.6 | 0.08 | 5.8E-04 |
| PSR B | Freq. range |
|
Q | PSR B | Freq. range |
|
Q | |||
| [GHz] | ||||||||||
| 1753-24 | 0.4 - 1.6 | -0.7 | 0.14 | 3.2E-01 | 1845-19 | 0.4 - 0.6 | -2.0 | 0.46 | ||
| 1754-24 | 0.4 - 1.4 | -1.1 | 0.09 | 9.1E-02 | 1846-06 | 0.4 - 1.4 | -2.2 | 0.10 | 8.4E-01 | |
| 1756-22 | 0.4 - 4.9 | -1.7 | 0.09 | 5.3E-01 | 1848+04 | 0.6 - 1.4 | -1.4 | |||
| 1757-24 | 0.4 - 0.6 | -3.6 | 1848+12 | 0.4 - 1.6 | -1.9 | 0.16 | 4.3E-02 | |||
| 1758-03 | 0.4 - 1.4 | -2.6 | 0.11 | 2.3E-01 | 1848+13 | 0.4 - 1.6 | -1.4 | 0.18 | 1.2E-01 | |
| 1758-23 | 1.4 - 4.9 | -2.5 | 0.10 | 8.3E-04 | 1849+00 | 1.4 - 4.9 | -2.4 | 0.12 | 4.8E-01 | |
| 1800-27 | 0.4 - 1.4 | -1.4 | 1851-14 | 0.4 - 0.6 | -0.8 | 0.42 | ||||
| 1802-07 | 0.4 - 1.4 | -1.3 | 0.31 | 1853+01 | 0.4 - 0.6 | -2.5 | ||||
| 1804-08 | 0.4 - 4.9 | -1.2 | 0.08 | 6.1E-07 | 1855+02 | 0.6 - 4.9 | -1.2 | 0.09 | 9.5E-02 | |
| 1804-27 | 0.6 - 1.4 | -3.0 | 0.21 | 1857-26 | 0.4 - 10.7 | -2.1 | 0.06 | 1.2E-03 | ||
| 1805-20 | 0.6 - 4.9 | -1.5 | 0.07 | 1859+01 | 0.4 - 0.6 | -2.9 | 0.21 | |||
| 1806-21 | 0.6 - 1.6 | -2.0 | 0.34 | 7.5E-02 | 1859+03 | 0.4 - 4.9 | -2.8 | 0.08 | 3.8E-02 | |
| 1810+02 | 0.4 - 1.4 | -1.7 | 0.21 | 3.1E-02 | 1859+07 | 0.4 - 1.6 | -1.0 | 0.15 | 8.2E-01 | |
| 1811+40 | 0.4 - 1.4 | -1.8 | 0.22 | 5.0E-02 | 1900+01 | 0.4 - 4.9 | -1.9 | 0.15 | 3.3E-01 | |
| 1813-17 | 0.6 - 1.6 | -1.0 | 0.14 | 5.0E-01 | 1900+05 | 0.4 - 4.9 | -1.7 | 0.08 | 3.9E-02 | |
| 1813-26 | 0.4 - 0.6 | -1.4 | 0.33 | 1900+06 | 0.4 - 4.9 | -2.2 | 0.10 | 1.4E-01 | ||
| 1815-14 | 0.9 - 1.6 | -1.6 | 0.22 | 8.5E-04 | 1900-06 | 0.4 - 0.6 | -1.8 | 0.19 | ||
| 1817-13 | 0.6 - 1.6 | -1.7 | 0.37 | 3.7E-01 | 1902-01 | 0.4 - 1.4 | -1.9 | 0.11 | 1.1E-02 | |
| 1817-18 | 0.4 - 1.4 | -1.1 | 0.27 | 1903+07 | 0.6 - 1.4 | -1.3 | 0.10 | 2.6E-01 | ||
| 1818-04 | 0.4 - 4.9 | -2.4 | 0.06 | 9.7E-02 | 1904+06 | 0.4 - 1.6 | -0.7 | 0.21 | 9.6E-01 | |
| 1819-22 | 0.4 - 1.4 | -1.7 | 0.07 | 2.1E-01 | 1905+39 | 0.4 - 1.4 | -2.0 | 0.16 | 9.0E-02 | |
| 1820-11 | 0.4 - 4.9 | -1.5 | 0.05 | 1.9E-04 | 1907+00 | 0.4 - 1.4 | -2.0 | 0.11 | 5.6E-08 | |
| 1820-14 | 0.6 - 1.4 | -0.7 | 0.22 | 1907+02 | 0.4 - 1.4 | -2.8 | 0.11 | 3.8E-02 | ||
| 1820-30B | 0.4 - 0.6 | -1.9 | 0.33 | 1907+03 | 0.4 - 4.9 | -1.8 | 0.07 | 1.4E-01 | ||
| 1820-31 | 0.4 - 1.4 | -2.1 | 0.20 | 4.8E-01 | 1907+10 | 0.4 - 1.4 | -2.5 | 0.09 | 5.6E-01 | |
| 1821+05 | 0.4 - 1.4 | -1.7 | 0.18 | 2.1E-02 | 1907-03 | 0.4 - 1.4 | -2.7 | 0.12 | 7.4E-05 | |
| 1821-11 | 0.6 - 4.9 | -2.3 | 0.10 | 1.2E-01 | 1910+20 | 0.4 - 1.4 | -1.6 | 0.16 | 5.9E-01 | |
| 1821-19 | 0.4 - 4.9 | -1.9 | 0.06 | 2.2E-01 | 1911+11 | 0.4 - 0.6 | -1.4 | |||
| 1822+00 | 0.4 - 1.4 | -2.4 | 0.26 | 4.0E-01 | 1911+13 | 0.4 - 4.9 | -1.5 | 0.06 | 8.5E-03 | |
| 1822-09 | 0.4 - 10.6 | -1.3 | 0.08 | 1.3E-02 | 1911-04 | 0.4 - 1.4 | -2.6 | 0.11 | 3.3E-01 | |
| 1822-14 | 1.4 - 4.9 | -0.7 | 0.08 | 3.6E-01 | 1913+10 | 0.4 - 1.6 | -1.9 | 0.15 | 5.6E-01 | |
| 1823-11 | 0.4 - 1.6 | -2.4 | 0.10 | 9.9E-01 | 1913+16 | 0.4 - 1.4 | -1.4 | 0.24 | ||
| 1823-13 | 0.6 - 10.6 | -0.6 | 1913+167 | 0.4 - 0.6 | -1.4 | 0.59 | ||||
| 1826-17 | 0.4 - 4.9 | -1.7 | 0.06 | 5.1E-05 | 1914+09 | 0.4 - 1.4 | -2.3 | 0.11 | 2.1E-03 | |
| 1828-10 | 0.4 - 1.6 | -0.4 | 0.14 | 2.3E-01 | 1914+13 | 0.4 - 4.9 | -1.6 | 0.10 | 3.0E-02 | |
| 1829-08 | 0.4 - 1.6 | -0.8 | 0.06 | 1.5E-04 | 1915+13 | 0.4 - 4.9 | -1.8 | 0.09 | 3.7E-02 | |
| 1829-10 | 0.4 - 1.6 | -1.3 | 0.15 | 1.4E-01 | 1916+14 | 0.4 - 1.4 | -0.3 | 0.43 | 1.0E+00 | |
| 1830-08 | 0.6 - 4.9 | -1.1 | 0.05 | 1.2E-21 | 1917+00 | 0.4 - 4.9 | -2.2 | 0.07 | 6.3E-01 | |
| 1831-00 | 0.4 - 0.6 | -1.4 | 1918+19 | 0.4 - 1.4 | -2.4 | 0.16 | 9.4E-01 | |||
| 1831-03 | 0.4 - 1.4 | -2.7 | 0.08 | 1.1E-04 | 1919+14 | 0.4 - 4.9 | -1.3 | 0.14 | 9.2E-01 | |
| 1831-04 | 0.4 - 4.9 | -1.3 | 0.07 | 9.5E-01 | 1919+21 | 0.4 - 4.9 | -2.6 | 0.04 | 0.0E+00 | |
| 1832-06 | 0.6 - 1.6 | -0.4 | 0.35 | 2.9E-01 | 1920+20 | 0.4 - 0.6 | -2.5 | 0.70 | ||
| 1834-04 | 0.6 - 1.6 | -1.9 | 0.30 | 5.8E-01 | 1920+21 | 0.4 - 4.9 | -2.2 | 0.07 | 2.8E-02 | |
| 1834-06 | 0.6 - 1.6 | -1.2 | 0.24 | 9.5E-01 | 1923+04 | 0.4 - 0.6 | -2.7 | 0.50 | ||
| 1834-10 | 0.4 - 1.6 | -2.1 | 0.09 | 3.1E-01 | 1924+16 | 0.4 - 1.4 | -1.5 | 0.16 | 2.9E-01 | |
| 1838-04 | 0.9 - 1.6 | -1.3 | 0.21 | 2.0E-01 | 1929+10 | 0.4 - 24 | -1.6 | 0.04 | 1.5E-07 | |
| 1839+09 | 0.4 - 1.4 | -2.0 | 0.07 | 3.1E-01 | 1929+20 | 0.4 - 1.4 | -2.5 | 0.22 | 7.4E-01 | |
| 1839+56 | 0.4 - 1.4 | -1.5 | 0.22 | 3.2E-01 | 1930+22 | 0.4 - 1.6 | -1.5 | 0.09 | 3.9E-02 | |
| 1839-04 | 0.4 - 1.6 | -1.6 | 0.08 | 1.7E-01 | 1931+24 | 0.4 - 0.6 | -4.0 | |||
| 1841-04 | 0.4 - 1.6 | -1.6 | 0.07 | 5.8E-03 | 1933+16 | 0.4 - 4.9 | -1.7 | 0.03 | 8.1E-03 | |
| 1841-05 | 0.6 - 4.9 | -1.7 | 0.10 | 5.3E-01 | 1935+25 | 0.4 - 1.4 | -0.7 | 0.20 | 5.6E-02 | |
| 1842+14 | 0.4 - 4.9 | -1.6 | 0.09 | 1.7E-02 | 1937-26 | 0.4 - 1.4 | -0.9 | 0.30 | 1.9E-01 | |
| 1842-02 | 0.6 - 1.6 | -0.9 | 0.27 | 4.1E-02 | 1940-12 | 0.4 - 1.4 | -2.4 | 0.20 | 5.1E-01 | |
| 1842-04 | 0.6 - 1.4 | -0.8 | 0.29 | 1.4E-01 | 1941-17 | 0.4 - 1.4 | -2.3 | 0.30 | ||
| 1844-04 | 0.4 - 4.9 | -2.2 | 0.06 | 8.2E-02 | 1942-00 | 0.4 - 1.4 | -1.8 | 0.17 | 2.5E-02 | |
| 1845-01 | 0.4 - 10.6 | -1.6 | 0.05 | 4.0E-01 | 1943-29 | 0.4 - 1.4 | -2.0 | 0.25 | 8.9E-01 |
| PSR B | Freq. range |
|
Q | PSR B | Freq. range |
|
Q | |||
| [GHz] | ||||||||||
| 1944+17 | 0.4 - 4.9 | -1.3 | 0.12 | 1.9E-01 | 2111+46 | 0.4 - 10.6 | -2.1 | 0.04 | 2.1E-02 | |
| 1946+35 | 0.4 - 4.9 | -2.4 | 0.04 | 6.9E-09 | 2113+14 | 0.4 - 1.4 | -1.9 | 0.13 | 3.7E-02 | |
| 1946-25 | 0.4 - 1.4 | -2.0 | 0.22 | 5.4E-01 | 2148+52 | 0.4 - 1.6 | -1.3 | 0.05 | 1.1E-04 | |
| 1951+32 | 0.4 - 1.6 | -1.6 | 0.11 | 5.2E-03 | 2148+63 | 0.4 - 2.7 | -1.8 | 0.09 | 1.1E-03 | |
| 1953+50 | 0.4 - 4.9 | -1.6 | 0.09 | 8.5E-01 | 2152-31 | 0.4 - 1.4 | -2.3 | 0.40 | 3.9E-01 | |
| 2000+32 | 0.4 - 4.9 | -1.1 | 0.04 | 3.1E-02 | 2154+40 | 0.4 - 4.9 | -1.6 | 0.09 | 3.6E-02 | |
| 2000+40 | 0.4 - 4.9 | -2.2 | 0.03 | 5.5E-30 | 2210+29 | 0.4 - 1.4 | -1.5 | 0.20 | 1.3E-01 | |
| 2002+31 | 0.4 - 1.4 | -1.7 | 0.06 | 2.3E-20 | 2217+47 | 0.4 - 4.9 | -2.6 | 0.19 | 4.5E-01 | |
| 2003-08 | 0.4 - 1.4 | -1.4 | 0.20 | 9.4E-02 | 2224+65 | 0.4 - 4.6 | -1.9 | 0.11 | 3.9E-01 | |
| 2016+28 | 0.4 - 10.6 | -2.2 | 0.04 | 4.7E-01 | 2227+61 | 0.4 - 1.4 | -2.6 | 0.10 | 5.7E-03 | |
| 2022+50 | 0.4 - 4.9 | -0.8 | 0.05 | 5.3E-01 | 2241+69 | 0.4 - 1.4 | -1.4 | 0.46 | 5.8E-01 | |
| 2027+37 | 0.4 - 1.4 | -2.5 | 0.10 | 4.6E-02 | 2255+58 | 0.4 - 4.9 | -2.1 | 0.07 | 1.0E+00 | |
| 2035+36 | 0.4 - 1.7 | -1.6 | 0.39 | 9.8E-01 | 2303+30 | 0.4 - 1.4 | -2.3 | 0.16 | 3.6E-03 | |
| 2036+53 | 0.4 - 1.4 | -2.0 | 0.27 | 2.2E-01 | 2303+46 | 0.4 - 1.6 | -1.6 | |||
| 2044+15 | 0.4 - 1.4 | -1.7 | 0.15 | 3.4E-03 | 2306+55 | 0.4 - 4.9 | -1.9 | 0.06 | 3.1E-01 | |
| 2045+56 | 0.4 - 1.4 | -2.4 | 2310+42 | 0.4 - 10.6 | -1.9 | 0.03 | 5.1E-05 | |||
| 2045-16 | 0.4 - 10.6 | -2.1 | 0.07 | 1.8E-01 | 2315+21 | 0.4 - 1.4 | -2.1 | 0.44 | 6.9E-01 | |
| 2053+21 | 0.4 - 1.4 | -0.8 | 0.35 | 2323+63 | 0.4 - 1.4 | -0.8 | 0.23 | 6.4E-02 | ||
| 2053+36 | 0.4 - 1.4 | -1.9 | 0.04 | 3.5E-03 | 2327-20 | 0.4 - 1.4 | -2.0 | 0.29 | 8.7E-01 | |
| 2106+44 | 0.4 - 4.9 | -1.4 | 0.06 | 7.5E-04 | 2334+61 | 0.4 - 1.4 | -1.7 | 0.23 | 6.3E-01 | |
| 2110+27 | 0.4 - 1.4 | -2.2 | 0.18 | 5.6E-01 | 2351+61 | 0.4 - 10.6 | -1.1 | 0.13 | 3.1E-01 |
| PSR B | Freq. range |
|
Q1 |
|
Q2 |
|
||
| [GHz] | [GHz] | |||||||
| 0136+57 | 0.4-4.9 | -1.1 | 0.13 | 8.7E-02 | -2.3 | 0.35 | 1.3E-02 | 1.0 |
| 0226+70 | 0.4-1.4 | -0.5 | 0.24 | 5.8E-01 | -4.0 | 0.85 | 0.9 | |
| 0301+19 | 0.4-4.9 | -0.9 | 0.38 | 5.0E-01 | -2.3 | 0.34 | 0.9 | |
| 0355+54 | 0.4-23.0 | -0.7 | 0.19 | 1.0E-02 | -1.2 | 0.04 | 3.9E-01 | 1.9 |
| 0540+23 | 0.4-32.0 | -0.3 | 0.14 | 8.3E-01 | -1.6 | 0.09 | 6.0E-05 | 1.4 |
| 0823+26 | 0.4-14.8 | -0.7 | 0.43 | 4.5E-01 | -2.1 | 0.08 | 3.1E-05 | 1.3 |
| 1237+25 | 0.4-10.7 | -0.9 | 0.19 | 7.4E-08 | -2.2 | 0.25 | 2.5E-04 | 1.4 |
| 1749-28 | 0.4-10.7 | -2.4 | 0.06 | 3.8E-02 | -4.3 | 0.36 | 1.5E-01 | 2.7 |
| 1800-21 | 0.4-4.9 | -0.2 | 0.07 | 1.3E-01 | -1.0 | 0.32 | 1.4 | |
| 1952+29 | 0.4-10.7 | -0.6 | 0.52 | 9.2E-01 | -2.7 | 0.10 | 6.8E-01 | 1.2 |
| 2011+38 | 0.4-4.9 | -0.9 | 0.13 | 1.5E-01 | -1.9 | 0.10 | 7.3E-03 | 1.4 |
| 2020+28 | 0.4-32.0 | -0.7 | 0.40 | 3.3E-01 | -1.9 | 0.17 | 6.9E-01 | 2.3 |
| 2021+51 | 0.4-23.0 | -0.8 | 0.20 | 1.8E-01 | -1.5 | 0.07 | 2.0E-01 | 2.6 |
| 2319+60 | 0.4-10.6 | -1.1 | 0.12 | 7.3E-07 | -2.1 | 0.05 | 6.6E-03 | 1.4 |
| 2324+60 | 0.4-4.9 | -1.2 | 0.12 | 5.8E-01 | -2.5 | 0.27 | 1.4 |
Copyright The European Southern Observatory (ESO)