In any 2D non-axisymmetric potential the main families of orbits are the
so-called loop and box (BT87). Which family dominates the orbital
structure depends mainly on the relative value of the rotational kinetic energy
with respect to the degree of flatness of the potential (see below). To
describe the problem in a more general context, let us consider a spatial
axisymmetric galaxy, where we assume that the potential depends on the position
through
![]() ,
,
![]() being cylindrical
coordinates and q<1 the semiaxis ratio of isopotential curves
in the Rz-plane. The potential is then
being cylindrical
coordinates and q<1 the semiaxis ratio of isopotential curves
in the Rz-plane. The potential is then
![]() where
where ![]() is a smooth function of its argument.
is a smooth function of its argument.
In any case, 3D motion reduces to 2D motion in Cartesian coordinates if we introduce the
effective potential
![]() ,
where
,
where
![]() is a global integral. As the second term is
the same for any
is a global integral. As the second term is
the same for any ![]() ,
we focus the attention on the motion of a star in the
2D potential
,
we focus the attention on the motion of a star in the
2D potential
![]() where x,y are coordinates in some
meridian plane by setting
where x,y are coordinates in some
meridian plane by setting
![]()
![]() . Alternatively,
. Alternatively, ![]() could represent the motion
in the equatorial plane (z=0) of a barlike galaxy, being then x,y
coordinates in the latter plane.
could represent the motion
in the equatorial plane (z=0) of a barlike galaxy, being then x,y
coordinates in the latter plane.
The equations of motion, in these variables, are
A "physical'' interpretation is the following. The angular momentum (or the
rotational kinetic energy) plays a crucial role in the existence of both
families of orbits. Indeed, take polar coordinates in the xy-plane:
![]() ,
,
![]() ,
so
,
so
![]() ,
where
,
where
![]() .
Due to the lack of
central symmetry, a test star will be acted by a torque
.
Due to the lack of
central symmetry, a test star will be acted by a torque
![]() .
If
.
If
![]() then for any r>0the torque is null at
then for any r>0the torque is null at ![]() ,
,
![]() (and
(and ![]() ,
,
![]() ), that is,
on the x and y axis. Recalling that
), that is,
on the x and y axis. Recalling that
![]() ,
where
,
where
![]() is the angular momentum of the star, we conclude that an orbit
with
is the angular momentum of the star, we conclude that an orbit
with
![]() will follow a rectilinear orbit along the x or y axis.
A simple inspection of the expression for N shows that the torque is negative
in the first and third quadrant, being positive in the others. Therefore, we
see why the x-axis periodic orbit is stable while the y-axis one is
unstable. The torque confines near the x-axis and pulls away near the
y-axis. On the other hand, a simple epicycle approximation (see BT87, Lees
& Schwarzschild 1992) shows that the 1:1 (circular) periodic orbit is
naturally stable for
will follow a rectilinear orbit along the x or y axis.
A simple inspection of the expression for N shows that the torque is negative
in the first and third quadrant, being positive in the others. Therefore, we
see why the x-axis periodic orbit is stable while the y-axis one is
unstable. The torque confines near the x-axis and pulls away near the
y-axis. On the other hand, a simple epicycle approximation (see BT87, Lees
& Schwarzschild 1992) shows that the 1:1 (circular) periodic orbit is
naturally stable for ![]() not too large.
not too large.
Let us recall that this description is true provided that ![]() is a smooth
function of
is a smooth
function of
![]() .
If the potential has a singularity or a cusp at the
origin, then the analysis may be different. Therefore the discussion given
above is suitable for potentials that are not "hard'' at the origin, that is,
those for which the deflection angle
.
If the potential has a singularity or a cusp at the
origin, then the analysis may be different. Therefore the discussion given
above is suitable for potentials that are not "hard'' at the origin, that is,
those for which the deflection angle
![]() is close to
is close to ![]() when
when
![]() (see BT87, MS89 for details).
(see BT87, MS89 for details).
Let us write the full Hamiltonian in polar coordinates
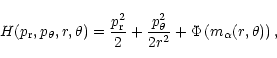
The unperturbed system is just a central field. So r oscillates
between two boundaries,
![]() ,
with frequency
,
with frequency
![]() ,
while
,
while
![]() varies on the circle
varies on the circle ![]() .
The frequency in the tangential direction is
.
The frequency in the tangential direction is
![]() where
where
![]() is, in general, irrational. The time
evolution of
is, in general, irrational. The time
evolution of ![]() can be written as
can be written as
![]() where
where ![]() is a
is a
![]() -periodic
function of time.
-periodic
function of time.
Let us focus the attention, in the perturbed system, on the dynamics in the
tangential direction. Keeping terms up to first order in ![]() in (3) we get
in (3) we get
Since ![]() is a measure of the amplitude of the torque, we conclude
that the relevant parameter that defines the orbital family is the relative
value of the rotational energy with respect to the strength of the
torque, which in turn depends on the degree of flatness of the potential.
is a measure of the amplitude of the torque, we conclude
that the relevant parameter that defines the orbital family is the relative
value of the rotational energy with respect to the strength of the
torque, which in turn depends on the degree of flatness of the potential.
From the above discussion it turns out that a limit angle,
![]() ,
could exist
,
could exist
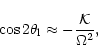
The frequency ![]() ,
depends on the average
,
depends on the average
![]() over
the unperturbed motion (Eqs. (6) and (8)). As defined
in (2), f1(r) can be put in terms of the circular speed,
over
the unperturbed motion (Eqs. (6) and (8)). As defined
in (2), f1(r) can be put in terms of the circular speed, ![]() :
:
![]() .
So from (8) follows that
.
So from (8) follows that

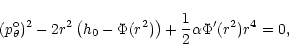
The invariant ![]() is in some sense local, since unperturbed orbits with
different angular momentum will have different values of the frequency:
is in some sense local, since unperturbed orbits with
different angular momentum will have different values of the frequency:
![]() .
From (9) and (10)
it is not difficult to conclude that the largest
.
From (9) and (10)
it is not difficult to conclude that the largest ![]() is expected for
minimum
is expected for
minimum
![]() ;
;
![]() ,
i.e., for
radial orbits, while the smallest one for maximum
,
i.e., for
radial orbits, while the smallest one for maximum
![]() ,
i.e., for circular orbits (see also Sect. 2.2).
,
i.e., for circular orbits (see also Sect. 2.2).
For the case of the 1:1 periodic orbit we can write,
One should remark that ![]() given by (8) was obtained
neglecting high order terms, assuming quasiperiodicity in the unperturbed
motion and averaging to zero the oscillating part. Thus the pendulum model is a
rough first approximation to the dynamics and other perturbing terms should be
present. However, the main effect of perturbations to the pendulum is to distort
somehow the invariant curves and to give rise to a stochastic layer around the
separatrix. That is, box and loop should be actually separated by a stochastic
layer instead of a separatrix. The larger the strength of
the perturbation, the larger is the width of the layer (for details about the
dynamics of the pendulum model and perturbation effects, see
Chirikov 1979).
given by (8) was obtained
neglecting high order terms, assuming quasiperiodicity in the unperturbed
motion and averaging to zero the oscillating part. Thus the pendulum model is a
rough first approximation to the dynamics and other perturbing terms should be
present. However, the main effect of perturbations to the pendulum is to distort
somehow the invariant curves and to give rise to a stochastic layer around the
separatrix. That is, box and loop should be actually separated by a stochastic
layer instead of a separatrix. The larger the strength of
the perturbation, the larger is the width of the layer (for details about the
dynamics of the pendulum model and perturbation effects, see
Chirikov 1979).
The derivation given above for ![]() is a justification of the invariant
introduced ad-hoc to compute certain models of elliptical galaxies that respect
a third integral. Indeed, if the potential has the form
is a justification of the invariant
introduced ad-hoc to compute certain models of elliptical galaxies that respect
a third integral. Indeed, if the potential has the form
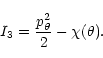
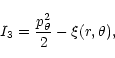
Note, however, that for a bar-like galaxy the multipolar expansion of
![]() has as dominant terms
has as dominant terms
The logarithmic potential has the form:
As we showed in the previous section, one of the main differences between loop and
box orbits is that the latter pass through the origin (projected on the
configuration space, the (x,y)-plane) while the former do not. Since for
boxes
![]() ,
,
![]() is a suitable choice for the
initial angular momentum for that orbits, while
is a suitable choice for the
initial angular momentum for that orbits, while
![]() is enough to ensure a loop orbit (see Eq. (8)
and discussion below). In Cartesian variables, since
is enough to ensure a loop orbit (see Eq. (8)
and discussion below). In Cartesian variables, since
![]() ,
in any case we can set, for instance, y0=0 and then px0=0for loops and x0=0 for boxes. Therefore, for the energy level h, x0 and
px0 parameterize, respectively, loop and box orbits. The same applies if
we exchange
,
in any case we can set, for instance, y0=0 and then px0=0for loops and x0=0 for boxes. Therefore, for the energy level h, x0 and
px0 parameterize, respectively, loop and box orbits. The same applies if
we exchange
![]() .
This choice of a single
Cartesian variable to label orbits in each family will help us later
(Sect. 4.2), but to investigate the connection between the actual
motion and the pendulum model, we will proceed with polar coordinates.
.
This choice of a single
Cartesian variable to label orbits in each family will help us later
(Sect. 4.2), but to investigate the connection between the actual
motion and the pendulum model, we will proceed with polar coordinates.
![\begin{figure}
{$q=0.9$\quad$q=0.8$\quad $q=0.7$ }
\includegraphics[angle=-90,wi...
...5mm]{H1686f2.ps}\includegraphics[angle=-90,width=61.5mm]{H1686f3.ps}\end{figure}](/articles/aas/full/2000/20/h1686/Timg189.gif) |
Figure 1:
Surfaces of section
|
A suitable map that should reveal the dynamics in the tangential direction is
a
![]() section for constant r and, for instance, with
section for constant r and, for instance, with
![]() .
Nevertheless one should ensure that the trajectory actually intersects
this surface. We expect that box orbits always cross any surface
.
Nevertheless one should ensure that the trajectory actually intersects
this surface. We expect that box orbits always cross any surface
![]() provided that
provided that
![]() .
However, this is not the case for all loop
orbits. For instance, in the limiting case when
.
However, this is not the case for all loop
orbits. For instance, in the limiting case when
![]() ,
the 1:1
periodic orbit becomes circular and it is fully contained in r=a.
Another restriction is that
,
the 1:1
periodic orbit becomes circular and it is fully contained in r=a.
Another restriction is that
![]() because, as mentioned,
for
because, as mentioned,
for
![]() ,
,
![]() is not well defined.
is not well defined.
In Fig. 1 we show
![]() surfaces of section for
surfaces of section for
![]() and three different values of q, 0.9, 0.8 and 0.7. Note that for
these values of q, the corresponding values of
and three different values of q, 0.9, 0.8 and 0.7. Note that for
these values of q, the corresponding values of ![]() are not small, 0.234,
0.562 and 1.04 respectively. Nevertheless the global motion resembles a pendulum
model. The origin corresponds to the long-axis periodic orbit while the
unstable points
are not small, 0.234,
0.562 and 1.04 respectively. Nevertheless the global motion resembles a pendulum
model. The origin corresponds to the long-axis periodic orbit while the
unstable points
![]() to the short-axis periodic orbit. The outermost
curves correspond to loop orbits relatively close to the 1:1 periodic orbit
(for both senses of rotation). Indeed, from (12) one immediately
finds that for this orbit
to the short-axis periodic orbit. The outermost
curves correspond to loop orbits relatively close to the 1:1 periodic orbit
(for both senses of rotation). Indeed, from (12) one immediately
finds that for this orbit
![]() ,
0.42, 0.38 for q=0.9, 0.8, 0.7
respectively. Because
,
0.42, 0.38 for q=0.9, 0.8, 0.7
respectively. Because ![]() ,
a gives an estimation of the mean value of
the semiaxis of this elliptic orbit (see Sect. 4.2 for a more
accurate determination).
,
a gives an estimation of the mean value of
the semiaxis of this elliptic orbit (see Sect. 4.2 for a more
accurate determination).
From Fig. 1 we see that box and loop families are separated by a
relatively narrow stochastic layer and, for large values of the angular
momentum, the latter is nearly an integral of motion. As q decreases from 0.9
the departures of the actual motion from the pendulum model become significant.
For instance, for q=0.7 we observe that the x-axis periodic orbit
becomes unstable and a bifurcation to a 2-periodic orbit appears
(see footnote at the end of next section). This sub-family of box family is
conformed by the well-known banana orbits (see, for instance, MS89). Note the
thin chaotic layer that separates bananas and boxes. We distinguish several
resonances and a comparatively large stochastic layer separates boxes and loops.
Some small islands are also present in the loop domain. Nevertheless, only a
few loop orbits appear in this figure (q=0.7) because almost all the
intersections with the surface
![]() correspond to box orbits.
Anyway the domain of box family increases against that of loops
as the flatness of the potential increases.
correspond to box orbits.
Anyway the domain of box family increases against that of loops
as the flatness of the potential increases.
![\begin{figure}
\par\includegraphics[angle=-90,width=84mm]{H1686f4.ps}\end{figure}](/articles/aas/full/2000/20/h1686/Timg198.gif) |
Figure 2:
|
In Fig. 2 we show the computed values of ![]() (actually
(actually ![]() )
for several (about 1500) orbits with initial conditions along the
)
for several (about 1500) orbits with initial conditions along the
![]() axis. We average
axis. We average
![]() over 1500 units
of time which is
over 1500 units
of time which is ![]() periods of the x-axis periodic orbit, using the
values of r obtained by solving the equations of motion corresponding
to (15) with q=0.9, 0.8, 0.7. We checked that the oscillating part,
g1(r(t)) - see Eq. (6) - averages to zero. For q=0.9 and 0.8
almost all orbits are either box or loop while for q=0.7, those for
periods of the x-axis periodic orbit, using the
values of r obtained by solving the equations of motion corresponding
to (15) with q=0.9, 0.8, 0.7. We checked that the oscillating part,
g1(r(t)) - see Eq. (6) - averages to zero. For q=0.9 and 0.8
almost all orbits are either box or loop while for q=0.7, those for
![]() belong to the banana sub-family (see Fig. 1). In
any case
belong to the banana sub-family (see Fig. 1). In
any case ![]() does not change too much over the whole range, less than by
a factor 2. This variation of
does not change too much over the whole range, less than by
a factor 2. This variation of ![]() can be computed
using (9), (10), (11) and (12). It is immediate that the
change in
can be computed
using (9), (10), (11) and (12). It is immediate that the
change in ![]() from radial (
from radial (
![]() )
to circular (maximum
)
to circular (maximum
![]() )
orbits is
)
orbits is
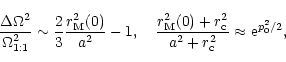
![\begin{figure}
\par\includegraphics[angle=-90,width=84mm]{H1686f5.ps}\end{figure}](/articles/aas/full/2000/20/h1686/Timg206.gif) |
Figure 3:
|
From this figure, for q=0.9 and 0.8 we see a similar, smooth behaviour of
![]() ,
except in those narrow intervals where a small island seems to be
present. Since the width of the stochastic layer for these two values of q is
rather small (particularly due to the fact that we are crossing the layer
through the thinest part), almost no evidence of its existence could be
inferred from the figure. However for q=0.7,
,
except in those narrow intervals where a small island seems to be
present. Since the width of the stochastic layer for these two values of q is
rather small (particularly due to the fact that we are crossing the layer
through the thinest part), almost no evidence of its existence could be
inferred from the figure. However for q=0.7, ![]() looks noisy in the
vicinity of the long-axis periodic orbit as well as on the separatrix,
revealing the existence of chaotic zones. Much more discontinuities can be also
observed, certainly due to the existence of many resonances. For the banana
family, as expected, the behaviour is different. In the latter case
looks noisy in the
vicinity of the long-axis periodic orbit as well as on the separatrix,
revealing the existence of chaotic zones. Much more discontinuities can be also
observed, certainly due to the existence of many resonances. For the banana
family, as expected, the behaviour is different. In the latter case ![]() is
almost constant in all this range. This can be understood looking back to
Fig. 1 and recalling that we are taking initial conditions along the
is
almost constant in all this range. This can be understood looking back to
Fig. 1 and recalling that we are taking initial conditions along the
![]() axis; in all cases the banana orbits are close to the marginal one.
axis; in all cases the banana orbits are close to the marginal one.
Having the small oscillation frequency we compute ![]() .
First we took a
set of representative orbits and we studied the time evolution of
.
First we took a
set of representative orbits and we studied the time evolution of ![]() .
We observed a nearly constant value of
.
We observed a nearly constant value of ![]() but, for box orbits, a
periodical peak structure was observed. This was not the case for loop orbits.
These peaks are due to the fact that
but, for box orbits, a
periodical peak structure was observed. This was not the case for loop orbits.
These peaks are due to the fact that ![]() is not an invariant when
is not an invariant when
![]() ;
all of them appeared at minimum r. To reduce their effect on the
instantaneous value of the invariant, we averaged
;
all of them appeared at minimum r. To reduce their effect on the
instantaneous value of the invariant, we averaged ![]() over the whole
time interval. This procedure, however, leads to slightly larger values of
over the whole
time interval. This procedure, however, leads to slightly larger values of
![]() due to the cumulative effect.
due to the cumulative effect.
In Fig. 3 we show the computed values of
![]() for the
same ensemble of orbits than in Fig. 2. For the long-axis periodic
orbit
for the
same ensemble of orbits than in Fig. 2. For the long-axis periodic
orbit
![]() (a zoom around
(a zoom around
![]() reveals that
the initial value of
reveals that
the initial value of
![]() also for q=0.7). The line
also for q=0.7). The line
![]() separates box and loop domains and a simple comparison
with Fig. 1 shows that the separatrix (to be precise, the stochastic
layer) is very close to that line. The maximum value observed for
separates box and loop domains and a simple comparison
with Fig. 1 shows that the separatrix (to be precise, the stochastic
layer) is very close to that line. The maximum value observed for ![]() is, in all cases, within the interval derived in (13).
is, in all cases, within the interval derived in (13).
![\begin{figure}
{$q=0.9$\quad$q=0.8$\quad$q=0.7$ }
\includegraphics[angle=-90,wid...
...=59mm]{H1686f7.ps}\includegraphics[angle=-90,width=59mm]{H1686f8.ps}\end{figure}](/articles/aas/full/2000/20/h1686/Timg210.gif) |
Figure 4:
Theoretical surfaces of section
|
Figure 3 is illustrative to show which family dominates the dynamics at
given level of energy and to identify other sub-families of the
principal ones. For instance, for q=0.9 box and loop orbits populate the
phase space and no other sub-family seems to be significant. On the other hand
for q=0.7 almost all the phase space is filled by box orbits but the
banana family occupies a fraction of the phase space (see Sect. 4.2).
Loops are scanty and some chaotic domains seems to become important. Recall
that the actual volume of the phase space occupied by any of these families
would not be measured by the size of the corresponding ![]() intervals.
We also include in Fig. 3 the theoretical value of
intervals.
We also include in Fig. 3 the theoretical value of ![]() which,
for the ensemble considered, is
which,
for the ensemble considered, is
![]() ,
where we take for
,
where we take for ![]() the computed values given in Fig. 2.
Note the good agreement between
the computed values given in Fig. 2.
Note the good agreement between ![]() and
and
![]() for loops and boxes
but, of course, they differ for the banana sub-family.
for loops and boxes
but, of course, they differ for the banana sub-family.
In Fig. 4 we show the surfaces of section,
![]() ,
computed using
,
computed using
![]() and
and ![]() obtained numerically. A comparison
with Fig. 1 reveals that the actual motion is well approximated by a
pendulum model for q=0.9 and for q=0.8, but the agreement is not so
good, as expected, for q=0.7.
obtained numerically. A comparison
with Fig. 1 reveals that the actual motion is well approximated by a
pendulum model for q=0.9 and for q=0.8, but the agreement is not so
good, as expected, for q=0.7.
Copyright The European Southern Observatory (ESO)