The eclipsing binary Y Sex
(also HD 87079, BD
![]() 2394, HIP 49217, PPM 156443,
AN 358.1934, FL 1156, P 3375;
2394, HIP 49217, PPM 156443,
AN 358.1934, FL 1156, P 3375;
![]() ,
,
![]()
![]() ,
,
![]() mag; Sp. F8)
is a relatively bright and well-known A-type contact binary
with an extremely low mass ratio.
It was discovered to be a variable star by Hoffmeister (1934).
Later, the system was observed photographically by Prikhodko (1947)
and Gaposchkin (1953).
The first photoelectric observations of Y Sex were presented by
Tanabe & Nakamura (1957) and Hill (1979) who derived a relatively
low value of the mass ratio of the components q = 0.175. Radial
velocities were obtained by McLean & Hilditch (1983), resulting
in
mag; Sp. F8)
is a relatively bright and well-known A-type contact binary
with an extremely low mass ratio.
It was discovered to be a variable star by Hoffmeister (1934).
Later, the system was observed photographically by Prikhodko (1947)
and Gaposchkin (1953).
The first photoelectric observations of Y Sex were presented by
Tanabe & Nakamura (1957) and Hill (1979) who derived a relatively
low value of the mass ratio of the components q = 0.175. Radial
velocities were obtained by McLean & Hilditch (1983), resulting
in
![]() ,
with good agreement with the photometrically
determined value. Herczeg (1993), in his period study, derived
these linear light elements:
,
with good agreement with the photometrically
determined value. Herczeg (1993), in his period study, derived
these linear light elements:
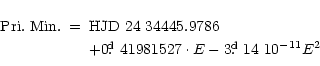
| System | Spectral | Period |
|
|
Reference |
| type | [days] | [10-10 days/cycle] | [
|
||
| AP Aur* | A2 | 0.56937 | 18.13 | 15.5 | Agerer & Splittgerber (1993) |
| BX Dra* | A3 | 0.57903 | 11.12 | ** | Agerer & Dahm (1995) |
| XY Boo | F5V | 0.37055 | 6.20 | 1.34 | Molík & Wolf (1998) |
| UZ Leo | A7 | 0.61804 | 6.07 | 1.30 | Hegedüs & Jäger (1992) |
| V839 Oph | F8V | 0.40900 | 3.46 | 3.31 | Wolf et al. (1996) |
| AH Vir | K0V | 0.40752 | 2.66 | 0.76 | Demircan et al. (1991) |
| GO Cyg * | B9+A0 | 0.71776 | 2.26 | 4.01 | Sezer et al. (1985), Rovithis (1997) |
| V401 Cyg | F0 | 0.58272 | 1.48 | 0.20 | this paper |
| 44 i Boo | G2V+G2V | 0.26782 | 1.24 | 1.15 | Gherega et al. (1994) |
| DK Cyg | A8V | 0.47069 | 1.15 | 0.29 | this paper |
| CT Eri | F0 | 0.63420 | 1.02 | 0.38 | Lipari & Sistero (1987) |
P3 (period) =
![]() days, i.e. 57.6 years;
days, i.e. 57.6 years;
T0 (time of periastron) = JD
![]() ;
;
A (semiamplitude) =
![]() day;
day;
e3 (eccentricity) =
![]() ;
;
![]() (length of periastron) =
(length of periastron) =
![]() .
.
These values were obtained together with the new mean linear ephemeris
![]()
![]()
![]()
by the least squares method.
Assuming a coplanar orbit (
![]() )
and a total mass
of the eclipsing pair according to the spectral type F8,
)
and a total mass
of the eclipsing pair according to the spectral type F8,
![]() (Harmanec 1988),
we can obtain a lower limit for the mass of the
third component
(Harmanec 1988),
we can obtain a lower limit for the mass of the
third component
![]() .
The value of the mass function
is
.
The value of the mass function
is
![]() ,
from which the minimum mass
of the third body follows as
,
from which the minimum mass
of the third body follows as
![]() .
A possible third component of spectral type M4-M5 with the bolometric
magnitude about +9.6 mag could be practically invisible
in this system with an F8 primary (
.
A possible third component of spectral type M4-M5 with the bolometric
magnitude about +9.6 mag could be practically invisible
in this system with an F8 primary (
![]() mag).
Therefore, new high-accuracy timings of this eclipsing binary are
necessary in order to confirm the light-time effect in this system.
mag).
Therefore, new high-accuracy timings of this eclipsing binary are
necessary in order to confirm the light-time effect in this system.
Copyright The European Southern Observatory (ESO)