A CR model with 80 levels for Fe VI is employed to calculate level
populations, Ni, relative to the ground level. The emitted flux
per ion for transition
![]() ,
or the emissivity
,
or the emissivity
![]() (ergs cm-3 s-1), is given by,
(ergs cm-3 s-1), is given by,
| (10) |
We can write the rate coupled equations of statistical equilibrium
in CR matrix form:
| (11) |
| (12) |
In a thermal continuum radiation field of optically thick
gaseous nebulae, the ion can be excited by photon
pumping or de-excited by induced emission.
With the FLE mechanism for excitation or de-excitation in the CR model,
Eqs. (10, 11) should be replaced by
| Cij | = | qijNe+JijBij (j>i) | |
| Cij | = | qijNe+Aij+JijBij (j<i) | (13) |
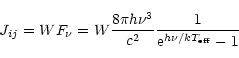 |
(14) |
With the notations used and explanations given above, the equation of statistical equlibrium for the k-th level has the form
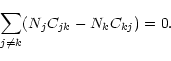 |
(15) |
The attenuation effect in continuum intensity Jij has been neglected in the above rate equations, i.e. there are no optical depths along the line of observation in the nebula to the continuum radiation source. This approximation may be responsible for part of the difference between the calculated and observed line ratios as shown in Table 6 below. With this approximation, the rate coefficients Cij are independent of level population Nk; the rate equations are therefore linear and can be solved directly.
Copyright The European Southern Observatory (ESO)