The EIE calculations are described in detail in CP99a,b, and compared with previous works. Below, we briefly summarise the qualitative aspects of those results. The next subsection discusses in detail the present calculations for the forbidden and allowed A-values for Fe VI.
With the exception of two calculations two decades ago, there were no other calculations until the recent work reported in CP99a,b. It is difficult to consider the relativistic effects together with the electron correlation effects in this complex atomic system, and the coupled channel calculations necessary for such studies are very computer intensive. The two previous sources for the excitation rates of Fe VI are the non-relativistic close coupling (CC) calculations by Garstang et al. (1978) and the distorted-wave (DW) calculations by Nussbaumer & Storey (1978). Although the Garstang et al. (1978) calculations were in the CC approximation, they used a very small basis set and did not obtain the resonance structures; their results are given only for the averaged values. The Nussbaumer & Storey (1978) calculations were in the DW approximations that does not enable a treatment of resonances. Therefore neither set of calculations included resonances or the coupling effects due to higher configurations. Owing primarily to these factors we find that the earlier excitation rates of Nussbaumer and Storey are lower by up to factors of three or more when compared to the new Fe VI rates presented in CP99b.
The target expansions in the present work are based on
the 34-term wave function expansion for Fe VI developed by Bautista (1996)
using the SUPERSTRUCTURE program in the non-relativistic
calculations for photoionization cross sections of Fe V.
The SUPERSTRUCTURE calculations for Fe VI were extended to include relativistic
fine structure using the Breit-Pauli Hamiltonian (Eissner et al. 1974;
Eissner 1998).
The designations for the 80 levels (34 LS terms)
dominated by the configurations
![]() ,
,
![]() and
and
![]() and their observed energies (Sugar & Corliss 1985),
are shown in Table 1.
and their observed energies (Sugar & Corliss 1985),
are shown in Table 1.
| i | Term | 2J | Energy | i | Term | 2J | Energy | |||
| 1 | 3d3 | 4F | 3 | 0.0 | 41 | 3d2(3F)4p | 4F |
5 | 3.101443 | |
| 2 | 5 | 0.004659 | 42 | 7 | 3.110750 | |||||
| 3 | 7 | 0.010829 | 43 | 9 | 3.120492 | |||||
| 4 | 9 | 0.018231 | 44 | 3d2(3F)4p | 2F |
5 | 3.121742 | |||
| 5 | 3d3 | 4P | 1 | 0.170756 | 45 | 7 | 3.131189 | |||
| 6 | 3 | 0.172612 | 46 | 3d2(3F)4p | 4D |
1 | 3.131290 | |||
| 7 | 5 | 0.178707 | 47 | 3 | 3.127568 | |||||
| 8 | 3d3 | 2G | 7 | 0.187870 | 48 | 5 | 3.137250 | |||
| 9 | 9 | 0.194237 | 49 | 7 | 3.147723 | |||||
| 10 | 3d3 | 2P | 1 | 0.241445 | 50 | 3d2(3F)4p | 2D |
3 | 3.140706 | |
| 11 | 3 | 0.238888 | 51 | 5 | 3.152138 | |||||
| 12 | 3d3 |
|
3 | 0.260877 | 52 | 3d2(3F)4p | 2G |
7 | 3.179977 | |
| 13 | 5 | 0.259568 | 53 | 9 | 3.189597 | |||||
| 14 | 3d3 | 2H | 9 | 0.261755 | 54 | 3d2(3P)4p | 2S |
1 | 3.205891 | |
| 15 | 11 | 0.266116 | 55 | 3d2(3P)4p | 4S |
3 | 3.240986 | |||
| 16 | 3d3 | 2F | 5 | 0.424684 | 56 | 3d2(1D)4p | 2P |
1 | 3.272354 | |
| 17 | 7 | 0.421163 | 57 | 3 | 3.260106 | |||||
| 18 | 3d3 | 2D1 | 3 | 0.656558 | 58 | 3d2(1D)4p | 2F |
5 | 3.265386 | |
| 19 | 5 | 0.653448 | 59 | 7 | 3.279505 | |||||
| 20 | 3d2(3F)4s | 4F | 3 | 2.386075 | 60 | 3d2(3P)4p | 4D |
1 | 3.275057 | |
| 21 | 5 | 2.390877 | 61 | 3 | 3.278569 | |||||
| 22 | 7 | 2.397871 | 62 | 5 | 3.287005 | |||||
| 23 | 9 | 2.406823 | 63 | 7 | 3.301248 | |||||
| 24 | 3d2(3F)4s | 2F | 5 | 2.452586 | 64 | 3d2(1D)4p | 2D |
3 | 3.297495 | |
| 25 | 7 | 2.466551 | 65 | 5 | 3.304281 | |||||
| 26 | 3d2(1D)4s | 2D | 3 | 2.562646 | 66 | 3d2(3P)4p | 4P |
1 | 3.316518 | |
| 27 | 5 | 2.559763 | 67 | 3 | 3.320593 | |||||
| 28 | 3d2(3P)4s | 4P | 1 | 2.565008 | 68 | 5 | 3.330627 | |||
| 29 | 3 | 2.570092 | 69 | 3d2(1G)4p | 2G |
7 | 3.326827 | |||
| 30 | 5 | 2.578448 | 70 | 9 | 3.328555 | |||||
| 31 | 3d2(3P)4s | 2P | 1 | 2.623713 | 71 | 3d2(3P)4p | 2D |
3 | 3.376592 | |
| 32 | 3 | 2.630266 | 72 | 5 | 3.376970 | |||||
| 33 | 3d2(1G)4s | 2G | 7 | 2.663908 | 73 | 3d2(1G)4p | 2H |
9 | 3.390785 | |
| 34 | 9 | 2.663752 | 74 | 11 | 3.405461 | |||||
| 35 | 3d2(1S)4s | 2S | 1 | 3.065870 | 75 | 3d2(3P)4p | 2P |
1 | 3.408944 | |
| 36 | 3d2(3F)4p | 4G |
5 | 3.082420 | 76 | 3 | 3.412018 | |||
| 37 | 7 | 3.093542 | 77 | 3d2(1G)4p | 2F |
5 | 3.454410 | |||
| 38 | 9 | 3.106829 | 78 | 7 | 3.444151 | |||||
| 39 | 11 | 3.123191 | 79 | 3d2(1S)4p | 2P |
1 | 3.719860 | |||
| 40 | 3d2(3F)4p | 4F |
3 | 3.094115 | 80 | 3 | 3.739745 |
| i | j |
|
|
i | j |
|
|
||
| 36 | 1 | 9.34e-02 | 9.68e-02 | 1.19e+09 | 80 | 2 | 9.64e-06 | 9.10e-06 | 2.70e+05 |
| 40 | 1 | 4.64e-01 | 4.68e-01 | 8.92e+09 | 36 | 3 | 2.91e-04 | 2.88e-04 | 3.68e+06 |
| 41 | 1 | 9.82e-02 | 9.85e-02 | 1.26e+09 | 37 | 3 | 2.14e-04 | 2.67e-04 | 2.04e+06 |
| 44 | 1 | 2.43e-03 | 2.50e-03 | 3.17e+07 | 38 | 3 | 1.75e-01 | 1.80e-01 | 1.34e+09 |
| 46 | 1 | 2.57e-01 | 2.55e-01 | 1.01e+10 | 41 | 3 | 1.05e-01 | 1.05e-01 | 1.34e+09 |
| 47 | 1 | 2.88e-02 | 2.89e-02 | 5.66e+08 | 42 | 3 | 9.02e-01 | 9.05e-01 | 8.71e+09 |
| 48 | 1 | 8.98e-04 | 8.83e-04 | 1.18e+07 | 43 | 3 | 8.20e-02 | 8.14e-02 | 6.37e+08 |
| 50 | 1 | 5.48e-02 | 5.40e-02 | 1.09e+09 | 44 | 3 | 8.66e-02 | 8.58e-02 | 1.12e+09 |
| 51 | 1 | 2.56e-03 | 2.50e-03 | 3.40e+07 | 45 | 3 | 2.86e-02 | 2.91e-02 | 2.80e+08 |
| 54 | 1 | 1.82e-06 | 1.86e-06 | 7.49e+04 | 48 | 3 | 5.06e-01 | 5.01e-01 | 6.62e+09 |
| 55 | 1 | 1.90e-08 | 1.54e-08 | 4.01e+02 | 49 | 3 | 3.99e-02 | 3.90e-02 | 3.95e+08 |
| 56 | 1 | 5.62e-03 | 5.89e-03 | 2.42e+08 | 51 | 3 | 8.14e-02 | 8.18e-02 | 1.07e+09 |
| 57 | 1 | 1.22e-04 | 1.29e-04 | 2.61e+06 | 52 | 3 | 6.25e-04 | 5.87e-04 | 6.30e+06 |
| 58 | 1 | 1.12e-04 | 1.09e-04 | 1.59e+06 | 53 | 3 | 1.30e-03 | 1.17e-03 | 1.06e+07 |
| 60 | 1 | 6.74e-02 | 7.11e-02 | 2.90e+09 | 58 | 3 | 1.12e-02 | 1.16e-02 | 1.58e+08 |
| 61 | 1 | 2.92e-02 | 3.06e-02 | 6.29e+08 | 59 | 3 | 6.04e-03 | 6.33e-03 | 6.48e+07 |
| 62 | 1 | 2.05e-03 | 2.14e-03 | 2.97e+07 | 62 | 3 | 1.71e-01 | 1.77e-01 | 2.45e+09 |
| 64 | 1 | 4.64e-04 | 4.80e-04 | 1.01e+07 | 63 | 3 | 2.73e-02 | 2.80e-02 | 2.97e+08 |
| 65 | 1 | 5.92e-05 | 5.99e-05 | 8.65e+05 | 65 | 3 | 3.28e-03 | 3.35e-03 | 4.77e+07 |
| 66 | 1 | 2.69e-05 | 2.67e-05 | 1.19e+06 | 68 | 3 | 1.32e-04 | 1.28e-04 | 1.95e+06 |
| 67 | 1 | 2.30e-05 | 2.23e-05 | 5.09e+05 | 69 | 3 | 9.30e-05 | 8.67e-05 | 1.03e+06 |
| 68 | 1 | 9.37e-07 | 8.67e-07 | 1.39e+04 | 70 | 3 | 1.45e-06 | 1.80e-07 | 1.28e+04 |
| 71 | 1 | 1.64e-04 | 1.37e-04 | 3.74e+06 | 72 | 3 | 2.46e-04 | 1.83e-04 | 3.74e+06 |
| 72 | 1 | 2.17e-05 | 1.86e-05 | 3.32e+05 | 73 | 3 | 2.64e-06 | 2.50e-06 | 2.42e+04 |
| 75 | 1 | 2.27e-05 | 1.54e-05 | 1.06e+06 | 77 | 3 | 1.38e-05 | 1.58e-05 | 2.19e+05 |
| 76 | 1 | 1.93e-06 | 1.28e-06 | 4.50e+04 | 78 | 3 | 7.28e-07 | 8.26e-07 | 8.62e+03 |
| 77 | 1 | 1.51e-05 | 1.87e-05 | 2.42e+05 | 37 | 4 | 8.83e-04 | 8.95e-04 | 8.38e+06 |
| 79 | 1 | 1.30e-05 | 1.26e-05 | 7.22e+05 | 38 | 4 | 1.59e-03 | 1.52e-03 | 1.22e+07 |
| 80 | 1 | 2.25e-06 | 2.15e-06 | 6.33e+04 | 39 | 4 | 1.86e-01 | 1.90e-01 | 1.20e+09 |
| 36 | 2 | 2.29e-03 | 2.47e-03 | 2.90e+07 | 42 | 4 | 7.97e-02 | 8.01e-02 | 7.66e+08 |
| 37 | 2 | 1.36e-01 | 1.41e-01 | 1.31e+09 | 43 | 4 | 1.29e+0 | 1.29e+0 | 1.00e+10 |
| 40 | 2 | 8.40e-02 | 8.49e-02 | 1.61e+09 | 45 | 4 | 3.29e-01 | 3.28e-01 | 3.20e+09 |
| 41 | 2 | 6.24e-01 | 6.27e-01 | 8.01e+09 | 49 | 4 | 6.18e-01 | 6.10e-01 | 6.07e+09 |
| 42 | 2 | 1.20e-01 | 1.19e-01 | 1.16e+09 | 52 | 4 | 8.53e-05 | 8.03e-05 | 8.57e+05 |
| 44 | 2 | 5.67e-03 | 5.86e-03 | 7.37e+07 | 53 | 4 | 4.35e-03 | 4.02e-03 | 3.52e+07 |
| 45 | 2 | 3.71e-03 | 3.76e-03 | 3.64e+07 | 59 | 4 | 5.10e-02 | 5.22e-02 | 5.45e+08 |
| 47 | 2 | 3.04e-01 | 3.01e-01 | 5.96e+09 | 63 | 4 | 2.30e-01 | 2.36e-01 | 2.49e+09 |
| 48 | 2 | 6.17e-02 | 6.10e-02 | 8.10e+08 | 69 | 4 | 3.62e-04 | 3.81e-04 | 3.97e+06 |
| 49 | 2 | 3.61e-04 | 3.41e-04 | 3.58e+06 | 70 | 4 | 5.33e-05 | 4.02e-05 | 4.70e+05 |
| 50 | 2 | 1.34e-01 | 1.34e-01 | 2.65e+09 | 73 | 4 | 2.09e-07 | 8.11e-08 | 1.91e+03 |
| 51 | 2 | 2.82e-02 | 2.79e-02 | 3.74e+08 | 74 | 4 | 1.18e-05 | 1.07e-05 | 9.04e+04 |
| 52 | 2 | 5.53e-04 | 4.96e-04 | 5.60e+06 | 78 | 4 | 1.12e-04 | 1.21e-04 | 1.32e+06 |
| 55 | 2 | 4.58e-07 | 4.10e-07 | 9.63e+03 | 40 | 5 | 8.03e-04 | 7.85e-04 | 1.38e+07 |
| 57 | 2 | 5.81e-04 | 6.07e-04 | 1.24e+07 | 46 | 5 | 1.14e-01 | 1.09e-01 | 4.03e+09 |
| 58 | 2 | 2.26e-03 | 2.43e-03 | 3.21e+07 | 47 | 5 | 8.80e-02 | 8.41e-02 | 1.54e+09 |
| 59 | 2 | 2.86e-04 | 2.88e-04 | 3.08e+06 | 50 | 5 | 2.53e-02 | 2.40e-02 | 4.48e+08 |
| 61 | 2 | 1.17e-01 | 1.22e-01 | 2.51e+09 | 54 | 5 | 1.56e-03 | 1.57e-03 | 5.78e+07 |
| 62 | 2 | 3.70e-02 | 3.84e-02 | 5.33e+08 | 55 | 5 | 1.66e-01 | 1.67e-01 | 3.15e+09 |
| 63 | 2 | 1.42e-03 | 1.47e-03 | 1.55e+07 | 56 | 5 | 1.88e-03 | 1.90e-03 | 7.28e+07 |
| 64 | 2 | 8.48e-04 | 8.65e-04 | 1.85e+07 | 57 | 5 | 5.31e-03 | 5.48e-03 | 1.02e+08 |
| 65 | 2 | 9.55e-04 | 9.84e-04 | 1.39e+07 | 60 | 5 | 2.36e-02 | 2.32e-02 | 9.15e+08 |
| 67 | 2 | 1.22e-04 | 1.21e-04 | 2.70e+06 | 61 | 5 | 2.81e-02 | 2.77e-02 | 5.46e+08 |
| 68 | 2 | 1.99e-05 | 1.81e-05 | 2.94e+05 | 64 | 5 | 1.97e-03 | 1.97e-03 | 3.88e+07 |
| 69 | 2 | 3.84e-06 | 2.14e-06 | 4.26e+04 | 66 | 5 | 1.95e-02 | 1.95e-02 | 7.75e+08 |
| 71 | 2 | 7.81e-05 | 5.55e-05 | 1.78e+06 | 67 | 5 | 8.78e-02 | 8.79e-02 | 1.75e+09 |
| 72 | 2 | 1.82e-04 | 1.48e-04 | 2.77e+06 | 71 | 5 | 2.20e-04 | 2.10e-04 | 4.55e+06 |
| 76 | 2 | 1.63e-05 | 1.15e-05 | 3.81e+05 | 75 | 5 | 3.78e-04 | 3.79e-04 | 1.59e+07 |
| 77 | 2 | 1.80e-06 | 1.96e-06 | 2.87e+04 | 76 | 5 | 4.32e-05 | 2.90e-05 | 9.11e+05 |
| 78 | 2 | 1.07e-05 | 1.33e-05 | 1.27e+05 | 79 | 5 | 2.11e-05 | 1.94e-05 | 1.07e+06 |
The weighted oscillator strength gf or the Einstein A-coefficient for a
dipole allowed fine-structure transition is proportional to the
generalised line strength (Seaton 1987) defined, in either length
form or velocity form, by the equations
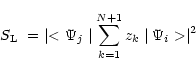 |
(1) |
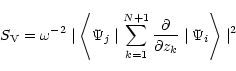 |
(2) |
Using the transition energy, Eij, between the initial and final states,
gifij and Aji for this transition can be obtained from S as
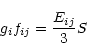 |
(3) |
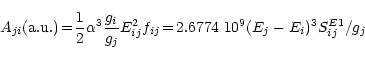 |
(4) |
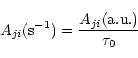 |
(5) |
We can use experimental transition energy
![]() to obtain refined
to obtain refined
![]() and
and
![]() values through
values through
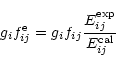 |
(6) |
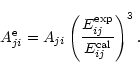 |
(7) |
The Breit-Pauli mode of the SUPERSTRUCTURE code was also used to
calculate the E2 and the M1transitions in Fe VI. The configuration expansion was adapted from that
used to optimise the lowest 34 LS terms by Bautista (1996). The
spectroscopic configurations,
the correlation configurations and the scaling
parameters
![]() for the Thomas-Fermi-Dirac-Amaldi type
potential of orbital nl are listed in Tables 3 and 4 of CP99a.
Much effort was devoted to choosing the correlation configurations
to optimise the target wavefunctions, within the constraint of
computational constraints associated with large memory requirements for
many of the
for the Thomas-Fermi-Dirac-Amaldi type
potential of orbital nl are listed in Tables 3 and 4 of CP99a.
Much effort was devoted to choosing the correlation configurations
to optimise the target wavefunctions, within the constraint of
computational constraints associated with large memory requirements for
many of the ![]() open shell configurations.
The primary criteria in this
selection are the level of agreement with the observed values for (a) the
level energies and fine structure splittings within the lowest LS terms,
and (b) the f-values for a number of the low lying dipole allowed
transitions.
Another practical criterion is that the calculated
A-values should be relatively stable with minor changes in scaling
parameters.
open shell configurations.
The primary criteria in this
selection are the level of agreement with the observed values for (a) the
level energies and fine structure splittings within the lowest LS terms,
and (b) the f-values for a number of the low lying dipole allowed
transitions.
Another practical criterion is that the calculated
A-values should be relatively stable with minor changes in scaling
parameters.
Like the procedure used in the calculation of the dipole allowed and
intercombination E1 gf-values,
the experimental level energies are also used
to improve the accuracy of the computed E2 and M1 transition
probabilities AE2 and AM1,
given as
| (8) |
and
| (9) |
The computed AE2 and AM1 for all 130 transitions among the
first 19 levels are given in Table 3.
| Transition | Present | Garstang et al. | NS | ||||
| i | j | E2 | M1 | E2 | M1 | E2 | M1 |
| 2 | 1 | 5.13e-11 | 5.76e-3 | 0.0 | 5.7e-3 | 4.97-11 | 5.74-3 |
| 5 | 1 | 6.04e-2 | 2.01e-4 | 8.3e-2 | 8.0e-5 | 5.97-2 | 3.31-4 |
| 6 | 1 | 1.27e-2 | 3.40e-3 | 1.7e-2 | 1.2e-3 | 1.26e-2 | 4.05e-3 |
| 7 | 1 | 7.15e-4 | 2.15e-4 | 1.0e-3 | 9.0e-5 | 7.04e-4 | 2.66e-4 |
| 8 | 1 | 1.90e-5 | 0.0 | 1.4e-5 | 0.0 | 1.66-5 | |
| 10 | 1 | 1.99e-3 | 1.54e-3 | 7.0e-3 | 7.3e-4 | 1.54e-3 | 1.99e-3 |
| 11 | 1 | 6.88e-4 | 3.70e-1 | 2.8e-3 | 1.19e-1 | 5.40e-4 | 3.56e-1 |
| 12 | 1 | 3.84e-4 | 3.77e-1 | 6.6e-4 | 4.01e-1 | 2.67e-4 | 3.86e-1 |
| 13 | 1 | 5.71e-7 | 4.97e-2 | 2.8e-6 | 3.36e-2 | 9.53e-7 | 4.34e-2 |
| 16 | 1 | 4.62e-3 | 1.97e-1 | 4.53e-3 | 2.23e-1 | ||
| 17 | 1 | 6.60e-4 | 0.0 | 6.55e-4 | |||
| 18 | 1 | 3.69e-3 | 8.60e-2 | 4.14e-3 | 1.26e-1 | ||
| 19 | 1 | 6.35e-4 | 4.97e-3 | 6.30e-4 | 9.44e-3 | ||
| 3 | 2 | 2.03e-10 | 1.34e-2 | 0.0 | 1.3e-2 | 1.99e-10 | 1.34e-2 |
| 4 | 2 | 6.46e-10 | 0.0 | ||||
| 5 | 2 | 3.47e-2 | 0.0 | 4.85e-2 | 0.0 | 3.42e-2 | |
| 6 | 2 | 3.35e-2 | 1.97e-3 | 4.59e-2 | 6e-4 | 3.32e-2 | 1.78e-3 |
| 7 | 2 | 5.69e-3 | 9.87e-4 | 7.9e-3 | 4.2e-4 | 5.63e-3 | 1.36e-3 |
| 8 | 2 | 1.63e-6 | 2.04e-1 | 1.6e-5 | 1.73e-1 | 1.74e-6 | 2.44e-1 |
| 9 | 2 | 6.00e-6 | 0.0 | 2e-6 | 0.0 | 4.71e-6 | |
| 10 | 2 | 3.19e-3 | 0.0 | 1.5e-3 | 0.0 | 2.75e-3 | |
| 11 | 2 | 3.39e-3 | 5.98e-1 | 6.4e-3 | 1.84e-1 | 2.78e-3 | 5.75e-1 |
| 12 | 2 | 7.96e-4 | 7.82e-1 | 1.2e-3 | 7.1e-1 | 5.37e-4 | 7.30e-1 |
| 13 | 2 | 2.95e-5 | 1.44e-1 | 2.1e-7 | 9.5e-2 | 2.79e-5 | 1.39e-1 |
| 14 | 2 | 2.59e-5 | 0.0 | 2.5e-5 | 0.0 | 2.70e-5 | |
| 16 | 2 | 9.77e-4 | 2.73e-2 | 1.09e-3 | 3.08e-2 | ||
| 17 | 2 | 1.90e-3 | 8.39e-2 | 1.70e-3 | 1.01e-1 | ||
| 18 | 2 | 2.77e-6 | 1.81e-1 | 1.21e-5 | 2.51e-1 | ||
| 19 | 2 | 2.05e-3 | 1.53e-2 | 2.11e-3 | 2.39e-2 | ||
| 4 | 3 | 3.66e-10 | 1.44e-2 | 0.0 | 1.4e-2 | 3.59e-10 | 1.45e-2 |
| 6 | 3 | 3.86e-2 | 0.0 | 5.4e-2 | 0.0 | 3.84e-2 | |
| 7 | 3 | 2.12e-2 | 2.39e-3 | 2.94e-2 | 9e-4 | 2.11e-2 | 2.63e-3 |
| 8 | 3 | 1.83e-5 | 2.19e-1 | 1.2e-5 | 1.85e-1 | 2.02e-5 | 2.61e-1 |
| 9 | 3 | 2.02e-6 | 2.20e-1 | 3.1e-5 | 1.86e-1 | 1.96e-6 | 2.51e-1 |
| 11 | 3 | 4.95e-3 | 0.0 | 6.1e-3 | 0.0 | 4.14e-3 | |
| 12 | 3 | 2.18e-3 | 0.0 | 5.3e-4 | 0.0 | 1.71e-3 | |
| 13 | 3 | 3.82e-4 | 1.12e+0 | 5e-5 | 7.29e-1 | 3.41e-4 | 1.07e+0 |
| 14 | 3 | 6.41e-5 | 2.20e-3 | 1.6e-5 | 4.3e-3 | 7.12e-5 | 4.12e-3 |
| 15 | 3 | 1.83e-5 | 0.0 | 5.0e-5 | 0.0 | 1.94e-5 | |
| 16 | 3 | 9.55e-4 | 3.57e-2 | 1.06e-3 | 3.78e-2 | ||
| 17 | 3 | 4.11e-4 | 1.49e-2 | 5.97e-4 | 1.70e-2 | ||
| 18 | 3 | 1.30e-2 | 0.0 | 1.57e-2 | |||
| 19 | 3 | 4.04e-3 | 1.64e-1 | 4.94e-3 | 2.45e-1 | ||
| 7 | 4 | 5.28e-2 | 0.0 | 7.3e-2 | 0.0 | 5.23e-2 | |
| 8 | 4 | 4.06e-6 | 1.26e-2 | 8.2e-6 | 1.1e-2 | 4.29e-6 | 1.34e-2 |
| 9 | 4 | 7.96e-5 | 5.39e-1 | 7.8e-5 | 4.55e-1 | 8.62e-5 | 6.24e-1 |
| 13 | 4 | 7.74e-4 | 0.0 | 5.1e-4 | 0.0 | 6.12e-4 | |
| 14 | 4 | 5.55e-6 | 3.35e-3 | 2.3e-5 | 7.8e-3 | 4.63e-6 | 6.86e-3 |
| 15 | 4 | 1.56e-4 | 6.73e-4 | 1.9e-4 | 5.7e-4 | 1.68e-4 | 1.01e-3 |
| 16 | 4 | 1.60e-4 | 0.0 | 2.04e-4 | |||
| 17 | 4 | 4.27e-3 | 2.17e-1 | 5.01e-3 | 2.56e-1 | ||
| 19 | 4 | 5.55e-2 | 0.0 | 6.41e-2 | |||
| 6 | 5 | 6.56e-13 | 1.86e-4 | 0.0 | 1.85e-4 | 6.64e-13 | 1.87e-4 |
| 7 | 5 | 5.71e-9 | 0.0 | ||||
| 10 | 5 | 0.0 | 4.42e-1 | 0.0 | 3.3e-1 | 3.76e-1 | |
| 11 | 5 | 6.09e-7 | 1.10e-1 | 2e-7 | 8.1e-2 | 4.88e-7 | 9.29e-2 |
| 12 | 5 | 3.67e-7 | 2.08e-2 | 1.26e-5 | 1.3e-3 | 1.71e-7 | 1.52e-2 |
| 13 | 5 | 3.22e-7 | 0.0 | 5.7e-6 | 0.0 | 2.84e-7 | |
| 16 | 5 | 8.51e-4 | 0.0 | 5.80e-4 | |||
| Transition | Present | Garstang et al. | NS | ||||
| i | j | E2 | M1 | E2 | M1 | E2 | M1 |
| 18 | 5 | 3.83e-2 | 1.26e-1 | 2.99e-2 | 1.37e-1 | ||
| 19 | 5 | 9.70e-3 | 0.0 | 7.16e-3 | |||
| 7 | 6 | 2.08e-9 | 4.70e-3 | 0.0 | 4.6e-3 | 2.09e-9 | 4.73e-3 |
| 10 | 6 | 1.46e-7 | 9.14e-6 | 1.5e-6 | 3.6e-5 | 2.21e-7 | 1.76e-5 |
| 11 | 6 | 3.61e-9 | 2.56e-1 | 9.5e-6 | 1.7e-1 | 1.69e-8 | 2.13e-1 |
| 12 | 6 | 1.00e-5 | 1.02e-2 | 5.4e-6 | 7.4e-4 | 8.43e-6 | 6.67e-3 |
| 13 | 6 | 7.01e-7 | 2.19e-3 | 5.4e-5 | 1.8e-3 | 5.06e-7 | 2.27e-3 |
| 16 | 6 | 1.30e-6 | 5.25e-4 | 2.13e-8 | 1.04e-3 | ||
| 17 | 6 | 3.04e-3 | 0.0 | 2.15e-3 | |||
| 18 | 6 | 1.05e-1 | 4.73e-1 | 8.08e-2 | 5.20e-1 | ||
| 19 | 6 | 1.02e-1 | 2.20e-1 | 7.71e-2 | 2.41e-1 | ||
| 8 | 7 | 4.85e-13 | 1.12e-10 | ||||
| 10 | 7 | 2.97e-6 | 0.0 | 1.0e-5 | 0.0 | 2.45e-6 | |
| 11 | 7 | 5.13e-6 | 1.14e-1 | 1.5e-5 | 1.19e-1 | 4.17e-6 | 1.00e-1 |
| 12 | 7 | 1.31e-6 | 2.19e-1 | 3.6e-6 | 7.4e-2 | 9.72e-7 | 1.76e-1 |
| 13 | 7 | 5.45e-6 | 7.98e-2 | 3.7e-6 | 4.3e-2 | 4.33e-6 | 6.71e-2 |
| 14 | 7 | 1.76e-9 | 0.0 | ||||
| 16 | 7 | 7.10e-5 | 2.32e-3 | 6.11e-5 | 5.47e-3 | ||
| 17 | 7 | 3.12e-4 | 2.11e-4 | 2.69e-4 | 4.95e-4 | ||
| 18 | 7 | 8.14e-4 | 1.06e-1 | 7.99e-4 | 1.23e-1 | ||
| 19 | 7 | 1.49e-3 | 1.30e+0 | 1.18e-3 | 1.41e+0 | ||
| 9 | 8 | 1.41e-12 | 4.03e-3 | 0.0 | 4e-3 | 1.71e-13 | 4.01e-3 |
| 11 | 8 | 1.12e-5 | 0.0 | 4.9e-6 | 0.0 | 7.85e-6 | |
| 12 | 8 | 6.73e-5 | 0.0 | 9.3e-5 | 0.0 | 5.13e-5 | |
| 13 | 8 | 5.80e-6 | 2.08e-6 | 9.6e-6 | 9e-6 | 3.89e-6 | 1.06e-5 |
| 14 | 8 | 1.82e-4 | 8.33e-2 | 1.9e-4 | 1.38e-1 | 1.59e-4 | 1.24e-1 |
| 15 | 8 | 5.32e-6 | 0.0 | 1.7e-5 | 0.0 | 4.28e-6 | |
| 16 | 8 | 1.47e-1 | 1.35e-1 | 1.49e-1 | 1.49e-1 | ||
| 17 | 8 | 1.24e-2 | 2.29e-1 | 1.24e-2 | 2.53e-1 | ||
| 18 | 8 | 1.25e+01 | 0.0 | 1.18e+1 | |||
| 19 | 8 | 9.45e-1 | 1.99e-3 | 9.07e-1 | 2.23e-3 | ||
| 13 | 9 | 5.83e-5 | 0.0 | 5.9e-5 | 0.0 | 4.08e-5 | |
| 14 | 9 | 2.32e-5 | 1.43e-1 | 0.0 | 2.35e-1 | 2.53e-5 | 2.11e-1 |
| 15 | 9 | 1.35e-4 | 7.84e-2 | 2.2e-4 | 1.29e-1 | 1.13e-4 | 1.16e-1 |
| 16 | 9 | 7.32e-5 | 0.0 | 2.06e-5 | |||
| 17 | 9 | 1.24e-1 | 1.07e-1 | 1.26e-1 | 1.17e-1 | ||
| 19 | 9 | 1.07e+1 | 0.0 | 1.00e+1 | |||
| 11 | 10 | 1.32e-12 | 2.19e-4 | 0.0 | 3.2e-4 | 1.21e-12 | 2.30e-4 |
| 12 | 10 | 3.15e-7 | 4.08e-2 | 4.0e-7 | 1.18e-2 | 2.94e-7 | 3.80e-2 |
| 13 | 10 | 7.59e-8 | 0.0 | 1e-7 | 0.0 | ||
| 16 | 10 | 1.63e-2 | 0.0 | 1.41e-2 | |||
| 18 | 10 | 1.54e+0 | 5.98e-3 | 1.43e+0 | 2.21e-3 | ||
| 19 | 10 | 6.28e-1 | 0.0 | 5.87e-1 | |||
| 12 | 11 | 5.15e-8 | 1.04e-1 | 3e-7 | 6.56e-2 | 5.89e-8 | 1.02e-1 |
| 13 | 11 | 8.66e-8 | 5.96e-2 | 8e-7 | 2.6e-2 | 1.10e-7 | 5.56e-2 |
| 16 | 11 | 1.05e-2 | 6.60e-3 | 1.07e-2 | 8.08e-3 | ||
| 17 | 11 | 2.26e-2 | 0.0 | 2.13e-2 | |||
| 18 | 11 | 2.11e+0 | 2.14e-2 | 2.08e+0 | 1.08e-2 | ||
| 19 | 11 | 6.72e-1 | 2.98e-1 | 6.63e-1 | 3.47e-1 | ||
| 13 | 12 | 7.95e-13 | 2.54e-5 | 0.0 | 3.4e-5 | 6.88e-13 | 2.70e-5 |
| 16 | 12 | 2.19e-2 | 5.41e-3 | 2.30e-2 | 7.71e-3 | ||
| 17 | 12 | 9.32e-4 | 0.0 | 4.44e-4 | |||
| 18 | 12 | 5.98e-2 | 9.58e-3 | 2.56e-2 | 3.81e-3 | ||
| 19 | 12 | 1.58e+0 | 2.69e-1 | 1.46e+0 | 3.09e-1 | ||
| 14 | 13 | 6.89e-15 | 0.0 | ||||
| 16 | 13 | 7.25e-3 | 2.75e-2 | 7.66e-3 | 3.63e-2 | ||
| 17 | 13 | 2.92e-2 | 1.02e-2 | 3.10e-2 | 1.36e-2 | ||
| 18 | 13 | 2.73e-1 | 7.48e-1 | 2.96e-1 | 8.64e-1 | ||
| 19 | 13 | 5.79e-1 | 4.77e-3 | 6.22e-1 | 4.80e-3 | ||
| 15 | 14 | 5.22e-11 | 1.33e-3 | 0.0 | 1.3e-3 | 5.33e-11 | 1.32e-3 |
| 16 | 14 | 7.02e-2 | 0.0 | 6.78e-2 | |||
| 17 | 14 | 1.20e-3 | 5.00e-4 | 8.85e-4 | 8.13e-4 | ||
| Transition | Present | Garstang et al. | NS | ||||
| i | j | E2 | M1 | E2 | M1 | E2 | M1 |
| 19 | 14 | 1.19e-1 | 0.0 | 1.50e-1 | |||
| 17 | 15 | 5.18e-2 | 0.0 | 4.99e-2 | |||
| 17 | 16 | 3.12e-12 | 8.88e-4 | 2.88e-12 | 8.86e-4 | ||
| 18 | 16 | 5.14e-1 | 3.95e-1 | 4.67e-1 | 3.72e-1 | ||
| 19 | 16 | 9.09e-2 | 6.41e-1 | 8.26e-2 | 6.01e-1 | ||
| 18 | 17 | 1.05e-1 | 0.0 | 9.67e-2 | |||
| 19 | 17 | 5.24e-1 | 3.73e-1 | 4.75e-1 | 3.50e-1 | ||
| 19 | 18 | 7.24e-11 | 6.42e-4 | 6.68e-11 | 6.41e-4 | ||
| i | j | E2 | M1 | i | j | E2 | M1 | i | j | E2 | M1 | i | j | E2 | M1 |
| 20 | 1 | 4.12e+4 | 6.84e-6 | 30 | 5 | 9.36e+3 | 0.0 | 26 | 10 | 8.54e+3 | 5.52e-5 | 33 | 14 | 6.87e+4 | 2.90e-3 |
| 21 | 1 | 2.68e+4 | 2.50e-5 | 31 | 5 | 0.0 | 2.86e-2 | 27 | 10 | 3.32e+3 | 0.0 | 34 | 14 | 1.68e+3 | 5.30e-3 |
| 22 | 1 | 2.51e+3 | 0.0 | 32 | 5 | 1.12e+2 | 6.88e-3 | 28 | 10 | 0.0 | 2.53e-4 | 22 | 15 | 1.19e+2 | 0.0 |
| 24 | 1 | 2.63e-1 | 7.50e-4 | 35 | 5 | 0.0 | 1.97e-4 | 29 | 10 | 8.11e+3 | 4.29e-6 | 23 | 15 | 1.49e+1 | 9.31e-7 |
| 25 | 1 | 3.57e-2 | 0.0 | 20 | 6 | 4.29e+3 | 3.09e-8 | 30 | 10 | 4.02e+3 | 0.0 | 25 | 15 | 5.88e+4 | 0.0 |
| 26 | 1 | 4.13e+3 | 8.11e-4 | 21 | 6 | 8.71e+3 | 1.42e-6 | 31 | 10 | 0.0 | 2.34e-4 | 33 | 15 | 2.31e+3 | 0.0 |
| 27 | 1 | 1.48e+2 | 7.62e-5 | 22 | 6 | 9.26e+3 | 0.0 | 32 | 10 | 1.07e+4 | 7.71e-5 | 34 | 15 | 6.46e+4 | 2.90e-3 |
| 28 | 1 | 4.20e+4 | 1.93e-6 | 24 | 6 | 1.64e+2 | 1.77e-7 | 35 | 10 | 0.0 | 3.08e-2 | 20 | 16 | 7.74e+0 | 1.87e-3 |
| 29 | 1 | 4.24e+3 | 9.91e-4 | 25 | 6 | 8.96e+1 | 0.0 | 20 | 11 | 2.65e+1 | 1.39e-4 | 21 | 16 | 2.15e+0 | 2.14e-4 |
| 30 | 1 | 2.52e+2 | 6.16e-5 | 26 | 6 | 1.03e+4 | 2.65e-4 | 21 | 11 | 7.38e+1 | 1.50e-4 | 22 | 16 | 1.96e+0 | 3.00e-4 |
| 31 | 1 | 3.18e+0 | 8.46e-6 | 27 | 6 | 1.35e+4 | 7.67e-4 | 22 | 11 | 1.33e+2 | 0.0 | 23 | 16 | 1.27e-1 | 0.0 |
| 32 | 1 | 8.58e-1 | 1.28e-8 | 28 | 6 | 5.62e+3 | 2.54e-3 | 24 | 11 | 1.74e+4 | 1.13e-4 | 24 | 16 | 4.36e+3 | 7.11e-6 |
| 33 | 1 | 1.58e+0 | 0.0 | 29 | 6 | 7.95e+3 | 4.01e-4 | 25 | 11 | 1.47e+3 | 0.0 | 25 | 16 | 4.18e+2 | 2.74e-3 |
| 35 | 1 | 1.71e+1 | 4.03e-8 | 30 | 6 | 1.09e+4 | 2.04e-3 | 26 | 11 | 9.61e+2 | 3.38e-4 | 26 | 16 | 5.33e+3 | 2.20e-4 |
| 20 | 2 | 3.94e+4 | 6.70e-5 | 31 | 6 | 1.01e+3 | 5.91e-6 | 27 | 11 | 1.21e+4 | 6.87e-4 | 27 | 16 | 1.29e+3 | 4.16e-4 |
| 21 | 2 | 2.23e+4 | 2.14e-6 | 32 | 6 | 2.00e+2 | 1.28e-2 | 28 | 11 | 1.44e+2 | 4.15e-5 | 28 | 16 | 3.22e+1 | 0.0 |
| 22 | 2 | 2.64e+4 | 5.43e-5 | 33 | 6 | 5.07e+0 | 0.0 | 29 | 11 | 5.10e+1 | 1.27e-4 | 29 | 16 | 4.78e+3 | 2.44e-4 |
| 23 | 2 | 1.58e+3 | 0.0 | 35 | 6 | 6.08e+1 | 5.35e-4 | 30 | 11 | 1.44e+4 | 6.58e-5 | 30 | 16 | 7.93e+2 | 2.95e-4 |
| 24 | 2 | 8.11e+1 | 1.59e-4 | 20 | 7 | 3.03e+2 | 1.62e-7 | 31 | 11 | 3.62e+4 | 1.53e-3 | 31 | 16 | 7.47e+4 | 0.0 |
| 25 | 2 | 8.71e+0 | 2.89e-4 | 21 | 7 | 1.82e+3 | 2.99e-8 | 32 | 11 | 8.82e+2 | 4.32e-3 | 32 | 16 | 1.05e+4 | 7.40e-6 |
| 26 | 2 | 1.35e+4 | 1.68e-3 | 22 | 7 | 6.14e+3 | 1.67e-6 | 33 | 11 | 7.35e+2 | 0.0 | 33 | 16 | 1.99e+4 | 2.94e-3 |
| 27 | 2 | 1.46e+3 | 1.66e-4 | 23 | 7 | 1.57e+4 | 0.0 | 35 | 11 | 1.35e+4 | 7.76e-3 | 34 | 16 | 1.63e+3 | 0.0 |
| 28 | 2 | 2.79e+4 | 0.0 | 24 | 7 | 1.35e+0 | 3.52e-7 | 20 | 12 | 1.05e+1 | 1.84e-4 | 35 | 16 | 1.65e+0 | 0.0 |
| 29 | 2 | 1.20e+4 | 1.59e-3 | 25 | 7 | 2.62e+1 | 1.38e-7 | 21 | 12 | 2.02e+1 | 1.89e-4 | 20 | 17 | 1.57e+0 | 0.0 |
| 30 | 2 | 2.16e+3 | 1.62e-4 | 26 | 7 | 1.97e+4 | 2.31e-3 | 22 | 12 | 1.15e+1 | 0.0 | 21 | 17 | 8.39e+0 | 4.87e-4 |
| 31 | 2 | 5.90e+1 | 0.0 | 27 | 7 | 7.67e+3 | 3.71e-4 | 24 | 12 | 4.20e+3 | 1.12e-4 | 22 | 17 | 4.52e+0 | 1.60e-4 |
| 32 | 2 | 1.83e+0 | 9.06e-6 | 28 | 7 | 5.16e+4 | 0.0 | 25 | 12 | 9.66e+3 | 0.0 | 23 | 17 | 2.32e+0 | 9.69e-4 |
| 33 | 2 | 9.02e-1 | 4.30e-4 | 29 | 7 | 1.67e+4 | 1.33e-3 | 26 | 12 | 1.58e+4 | 3.10e-4 | 24 | 17 | 8.42e+2 | 4.30e-3 |
| 34 | 2 | 4.37e-1 | 0.0 | 30 | 7 | 8.72e+3 | 1.20e-4 | 27 | 12 | 6.28e+2 | 2.44e-4 | 25 | 17 | 5.30e+3 | 2.47e-6 |
| 35 | 2 | 1.07e+1 | 0.0 | 31 | 7 | 4.13e+1 | 0.0 | 28 | 12 | 2.46e+0 | 8.28e-4 | 26 | 17 | 1.34e+3 | 0.0 |
| 20 | 3 | 4.85e+3 | 0.0 | 32 | 7 | 7.14e+1 | 2.29e-2 | 29 | 12 | 1.98e+4 | 1.02e-3 | 27 | 17 | 7.05e+3 | 1.73e-4 |
| 21 | 3 | 3.42e+4 | 7.43e-5 | 33 | 7 | 1.15e+0 | 1.19e-8 | 30 | 12 | 1.14e+3 | 1.46e-7 | 29 | 17 | 2.32e+3 | 0.0 |
| 22 | 3 | 3.42e+4 | 4.87e-7 | 34 | 7 | 1.33e+1 | 0.0 | 31 | 12 | 8.56e+2 | 1.40e-3 | 30 | 17 | 4.42e+3 | 1.16e-4 |
| 23 | 3 | 1.92e+4 | 5.77e-5 | 35 | 7 | 1.03e+2 | 0.0 | 32 | 12 | 2.18e+4 | 1.60e-3 | 32 | 17 | 6.00e+4 | 0.0 |
| 24 | 3 | 1.39e+1 | 7.62e-5 | 20 | 8 | 3.60e+1 | 0.0 | 33 | 12 | 1.08e+3 | 0.0 | 33 | 17 | 2.56e+3 | 6.63e-3 |
| 25 | 3 | 1.12e+2 | 5.86e-5 | 21 | 8 | 2.84e+1 | 6.92e-7 | 35 | 12 | 1.73e+4 | 7.24e-3 | 34 | 17 | 2.11e+4 | 3.02e-3 |
| 26 | 3 | 1.85e+4 | 0.0 | 22 | 8 | 3.39e+1 | 3.79e-6 | 20 | 13 | 4.21e-2 | 5.84e-5 | 20 | 18 | 9.03e-2 | 6.88e-5 |
| 27 | 3 | 6.86e+3 | 1.79e-3 | 23 | 8 | 4.37e+0 | 2.34e-7 | 21 | 13 | 6.17e-3 | 7.29e-5 | 21 | 18 | 1.49e+0 | 7.92e-5 |
| 29 | 3 | 1.70e+4 | 0.0 | 24 | 8 | 5.13e+4 | 1.57e-3 | 22 | 13 | 2.83e+0 | 4.27e-4 | 22 | 18 | 1.79e-1 | 0.0 |
| 30 | 3 | 9.20e+3 | 1.12e-3 | 25 | 8 | 5.08e+3 | 2.61e-3 | 23 | 13 | 3.95e+1 | 0.0 | 24 | 18 | 1.91e+3 | 5.14e-4 |
| 32 | 3 | 5.14e+1 | 0.0 | 26 | 8 | 2.18e+4 | 0.0 | 24 | 13 | 3.25e+3 | 4.91e-4 | 25 | 18 | 3.05e+2 | 0.0 |
| 33 | 3 | 3.68e+0 | 5.18e-4 | 27 | 8 | 2.78e+3 | 6.25e-6 | 25 | 13 | 1.95e+4 | 2.33e-4 | 26 | 18 | 2.74e-1 | 1.55e-7 |
| 34 | 3 | 1.39e-1 | 4.18e-4 | 29 | 8 | 2.42e+4 | 0.0 | 26 | 13 | 5.49e+3 | 1.78e-3 | 27 | 18 | 2.07e+1 | 1.74e-3 |
| 21 | 4 | 2.56e+3 | 0.0 | 30 | 8 | 1.98e+3 | 3.17e-6 | 27 | 13 | 1.80e+4 | 1.47e-3 | 28 | 18 | 1.00e-1 | 1.11e-6 |
| 22 | 4 | 2.33e+4 | 3.83e-5 | 32 | 8 | 1.50e+2 | 0.0 | 28 | 13 | 1.86e+2 | 0.0 | 29 | 18 | 1.03e+1 | 1.57e-6 |
| 23 | 4 | 6.63e+4 | 3.92e-7 | 33 | 8 | 2.98e+4 | 3.66e-9 | 29 | 13 | 7.66e+3 | 8.91e-6 | 30 | 18 | 6.96e+0 | 1.15e-3 |
| 24 | 4 | 6.64e+0 | 0.0 | 34 | 8 | 2.61e+3 | 3.57e-6 | 30 | 13 | 1.38e+4 | 2.22e-3 | 31 | 18 | 1.75e+4 | 2.77e-6 |
| 25 | 4 | 1.56e+1 | 9.41e-4 | 21 | 9 | 5.39e+1 | 0.0 | 31 | 13 | 6.57e+3 | 0.0 | 32 | 18 | 9.36e+3 | 2.45e-6 |
| 27 | 4 | 2.07e+4 | 0.0 | 22 | 9 | 1.80e+1 | 6.01e-6 | 32 | 13 | 1.20e+4 | 1.77e-3 | 33 | 18 | 7.33e+3 | 0.0 |
| 30 | 4 | 2.88e+4 | 0.0 | 23 | 9 | 5.95e+1 | 1.57e-7 | 33 | 13 | 1.55e+2 | 2.46e-6 | 35 | 18 | 4.70e+4 | 5.07e-8 |
| 33 | 4 | 7.33e-1 | 2.94e-5 | 24 | 9 | 1.07e+4 | 0.0 | 34 | 13 | 2.05e+3 | 0.0 | 20 | 19 | 6.10e-2 | 1.49e-5 |
| 34 | 4 | 1.21e+1 | 1.19e-3 | 25 | 9 | 4.87e+4 | 1.31e-3 | 35 | 13 | 4.51e+4 | 0.0 | 21 | 19 | 8.13e-1 | 5.63e-6 |
| 20 | 5 | 1.07e+4 | 1.55e-7 | 27 | 9 | 2.20e+4 | 0.0 | 21 | 14 | 1.09e+2 | 0.0 | 22 | 19 | 2.28e+0 | 6.04e-5 |
| 21 | 5 | 4.78e+3 | 0.0 | 30 | 9 | 1.72e+4 | 0.0 | 22 | 14 | 2.36e+1 | 6.08e-7 | 23 | 19 | 3.46e-2 | 0.0 |
| 24 | 5 | 2.55e+1 | 0.0 | 33 | 9 | 8.36e+2 | 8.76e-5 | 23 | 14 | 2.01e+0 | 2.23e-6 | 24 | 19 | 4.45e+2 | 1.69e-3 |
| 26 | 5 | 9.80e+2 | 2.75e-4 | 34 | 9 | 3.35e+4 | 1.05e-4 | 24 | 14 | 5.53e+4 | 0.0 | 25 | 19 | 2.46e+3 | 8.39e-4 |
| 27 | 5 | 8.16e+3 | 0.0 | 20 | 10 | 3.97e+1 | 1.06e-7 | 25 | 14 | 5.14e+3 | 7.81e-6 | 26 | 19 | 3.22e+1 | 1.91e-3 |
| 28 | 5 | 0.0 | 2.17e-5 | 21 | 10 | 2.69e+1 | 0.0 | 27 | 14 | 8.39e+2 | 0.0 | 27 | 19 | 6.67e+0 | 9.49e-6 |
| 29 | 5 | 2.04e+3 | 1.39e-3 | 24 | 10 | 6.36e+3 | 0.0 | 30 | 14 | 5.22e+2 | 0.0 | 28 | 19 | 8.86e+0 | 0.0 |
Copyright The European Southern Observatory (ESO)