The PSF is not needed with MVM. This is an advantage when the PSF is unknown, or difficult to estimate, which happens relatively often when it is space-variant. However, when the PSF is well-determined, it becomes a drawback because known information is not used for the object reconstruction. This can lead to systematic errors in the photometry, which depends on the PSF and on the source signal to noise ratio. In order to preempt such a bias, a kind of calibration must be performed using simulations (Starck et al. 1999). This section shows how the PSF can be used in the MVM, leading to a deconvolution.
Consider an image characterized by its intensity
distribution (the "data'') I(x,y), corresponding to the observation
of a
"real image'' O(x,y) through an optical system. If the
imaging system is linear and shift-invariant, the relation between
the object and the image in the same coordinate frame is a
convolution:
A reconstructed and deconvolved object can be obtained
by searching for a signal O such that
the wavelet coefficients of P*O are the same as those of the
detected
structures. If ![]() describes the wavelet transform operator,
and
describes the wavelet transform operator,
and ![]() the projection operator in the subspace of the detected
coefficients,
the solution is found by minimization of
the projection operator in the subspace of the detected
coefficients,
the solution is found by minimization of
Any minimizing method can be used to obtain the solution O. Since we did
not
find any problem of convergence, noise amplification, or ringing
effect,
we chose the van Cittert method on the grounds of its simplicity.
For each detected object, we apply the following algorithm:
| (5) |
Deconvolution methods generally do not take into account the case of space-variant PSF. The standard approach when the PSF varies is to decompose the image into blocks, and to consider the PSF constant inside a given block. Blocks which are too small lead to a problem of computation time (the FFT cannot be used), while blocks which are too large introduce errors due to the use of an incorrect PSF. Blocking artifacts may also appear. Combining source detection and deconvolution opens up an elegant way for deconvolution with a space-variant PSF. Indeed, a straightforward method is derived by just replacing the constant PSF at step 3 of the algorithm with the PSF at the centre of the object. This means that it is not the image which is deconvolved, but its constituent objects.
In many cases, there is no sense in trying to deconvolve an image at the resolution of the pixel (especially when the PSF is very large). The idea to limit the resolution is relatively old, because it is already this concept which is used in the CLEAN algorithm (Högbom 1974). Indeed the Clean-Beam fixes the resolution in the final solution. This principle was also developed by Lannes (1987) in a different form. This concept has been re-invented, first by Gull & Skilling (1991) who have called the Clean-Beam the Intrinsic Correlation Function (ICF), and more recently by Magain (1998) and Pijpers (1999).
The ICF is usually a Gaussian, but in some cases it may be useful to take another function. For example, if we want to compare two images I1 and I2 which are obtained with two wavelengths or with two different instruments, their PSFs P1 and P2 will certainly be different. The classic approach would be to deconvolve I1 with P2 and I2 with P1, so we are sure that both are at the same resolution. But unfortunately we lose some resolution in doing this. Deconvolving both images is generally not possible because we can never be sure that both solutions O1 and O2 will have the same resolution.
A solution would be to
deconvolve only the image which has the worse resolution
(say I1), and to limit the deconvolution to the second image
resolution (I2).
Then, we just have to take P2 for the ICF. The deconvolution problem
is to
find ![]() (hidden solution) such that:
(hidden solution) such that:
| (6) |
Introducing an ICF G in the deconvolution equation leads to
just considering a
new PSF ![]() which is the convolution of P and G.
The deconvolution is carried out using
which is the convolution of P and G.
The deconvolution is carried out using ![]() ,
and the solution
must be
reconvolved with G at the end. In this way, the solution has a constrained
resolution, but aliasing may occur during the iterative process, and it
is
not sure that the artifacts will disappear afer the re-convolution with
G.
Magain (1998) has proposed an original alternative to
this
problem, by assuming that the PSF can be considered as the convolution
product of two terms, the ICF G and an unknown S, P=G*S. Using
S instead of P in the deconvolution process, and a sufficiently large
FWHM value for G, implies that the
Shannon sampling theorem (Shannon 1948) is never
violated. But the problem is now to calculate S, knowing P and G,
which is again a deconvolution problem. Unfortunately,
this delicate point was not discussed in the original paper. Propagation
of the error on the S estimation in the final solution has also until now
not been investigated, even if this issue seems to be quite
important.
,
and the solution
must be
reconvolved with G at the end. In this way, the solution has a constrained
resolution, but aliasing may occur during the iterative process, and it
is
not sure that the artifacts will disappear afer the re-convolution with
G.
Magain (1998) has proposed an original alternative to
this
problem, by assuming that the PSF can be considered as the convolution
product of two terms, the ICF G and an unknown S, P=G*S. Using
S instead of P in the deconvolution process, and a sufficiently large
FWHM value for G, implies that the
Shannon sampling theorem (Shannon 1948) is never
violated. But the problem is now to calculate S, knowing P and G,
which is again a deconvolution problem. Unfortunately,
this delicate point was not discussed in the original paper. Propagation
of the error on the S estimation in the final solution has also until now
not been investigated, even if this issue seems to be quite
important.
This section describes how to calculate the FWHMfor a given sampling, in order not to violate the Shannon
sampling theorem. Gaussian functions are generally chosen for the ICF.
The resolution to be
achieved is fixed by its standard deviation
![]() ,
or its FWHM(FWHM=2.34
,
or its FWHM(FWHM=2.34
![]() ). Since the Fourier transform of a Gaussian
of standard deviation
). Since the Fourier transform of a Gaussian
of standard deviation
![]() is
also a Gaussian of standard deviation
is
also a Gaussian of standard deviation
![]() ,
(N being the number of pixels), we can estimate the smallest FWHM
which
does not violate the Shannon sampling theorem.
In theory, a Gaussian cannot respect it,
but in practice we can consider that values smaller than a given
,
(N being the number of pixels), we can estimate the smallest FWHM
which
does not violate the Shannon sampling theorem.
In theory, a Gaussian cannot respect it,
but in practice we can consider that values smaller than a given
![]() have no practical effect, and the Shannon sampling theorem is
experimentally
respected if
have no practical effect, and the Shannon sampling theorem is
experimentally
respected if
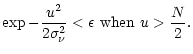 |
(7) |
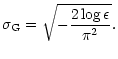 |
(8) |
| ICF
|
ICF FWHM | |
| 10-3 | 1.18 | 2.77 |
| 10-4 | 1.37 | 3.20 |
| 10-5 | 1.53 | 3.57 |
| 10-7 | 1.81 | 4.23 |
| 10-10 | 2.16 | 5.05 |
| 10-20 | 3.05 | 7.15 |
If the PSF is undersampled, it can be used in the same way, but results
may not be optimal due to the fact that the sampled PSF varies
depending on the position of the source. If an oversampled PSF is available,
resulting from theoretical calculation or from a set of observations,
it should be used to improve the solution. In this case, each reconstructed
object will be oversampled. Equation (4) must be replaced by
Copyright The European Southern Observatory (ESO)