The wavelet transform of an image by the à trous algorithm
produces, at each scale j, a set ![]() .
This has
the same number of pixels as the image. The original image
c0 can be expressed as the sum of all the wavelet scales and the
smoothed array
.
This has
the same number of pixels as the image. The original image
c0 can be expressed as the sum of all the wavelet scales and the
smoothed array ![]() by the expression
by the expression
![]() .
A pixel at position x,y can be expressed also as the sum of all
the
wavelet coefficients at this position, plus the smoothed array:
.
A pixel at position x,y can be expressed also as the sum of all
the
wavelet coefficients at this position, plus the smoothed array:
![]() .
.
After applying the wavelet transform on the image, we have to detect, to extract, to measure and to recognize the significant structures. This is done by first computing the multiresolution support of the image, and by applying a segmentation scale by scale. The wavelet space of a 2D direct space is a 3D one. An object has to be defined in this space. A general idea for object definition lies in the connectivity property. An object occupies a physical region, and in this region we can join any pixel to other ones. Connectivity in direct space has to be transported to wavelet transform space (WTS). In order to define the objects we have to identify the WTS pixels we can attribute to the objects. We describe in this section the different steps of this method.
The Multiscale Vision Model (MVM) (Bijaoui & Rué 1995; Rué & Bijaoui 1997) described an object as a hierarchical set of structures. It uses the following definitions:
A multiresolution support of an image describes in a
logical or Boolean way if an image I contains information at a
given scale j and at a given position (x,y).
If
M(I)(j,x,y) = 1 (or ![]() ), then I contains information
at
scale j and at the position (x,y).
M depends on several parameters:
), then I contains information
at
scale j and at the position (x,y).
M depends on several parameters:
The multiresolution support of an image is computed in several steps:
The multiresolution support will be obtained by detecting
at each scale the significant coefficients.
The multiresolution support is defined by:
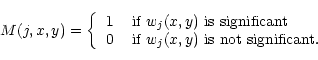 |
(1) |
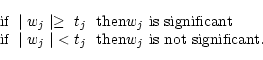 |
(2) |
An object is described as a hierarchical set of structures.
The rule which allows us to connect two structures into a single object
is called "interscale relation''. Figure 2 shows
how
several structures at different scales are linked together, and form
objects.
We have now to define the interscale relation:
let us consider two structures at two successive scales, Skj and
Slj+1. Each
structure is located in one of the individual images of the
decomposition and corresponds to a region in this image where the
signal is significant. Denoting ![]() the pixel position of the maximum
wavelet coefficient value of Skj, Skj is said to be connected
to
Slj+1 if Slj+1 contains the pixel position
the pixel position of the maximum
wavelet coefficient value of Skj, Skj is said to be connected
to
Slj+1 if Slj+1 contains the pixel position ![]() (i.e.
the maximum
position of the structure Skj must also be contained in the
structure
Slj+1).
Several structures
appearing in successive wavelet coefficient images can be connected in
such a way, which we call an object in the interscale connectivity
graph.
(i.e.
the maximum
position of the structure Skj must also be contained in the
structure
Slj+1).
Several structures
appearing in successive wavelet coefficient images can be connected in
such a way, which we call an object in the interscale connectivity
graph.
Hence, a set of structures defines an object W = Skj, ...Sk'j' which can be reconstructed separately from other objects. The coaddition of all reconstructed objects is a filtered version of the input data.
The reconstruction problem
consists of searching for a signal O such that
its wavelet coefficients are the same as those of the detected
structures. If ![]() describes the wavelet transform operator, and
describes the wavelet transform operator, and
![]() the
projection operator in the subspace of the detected coefficients
(i.e. having set to zero all coefficients at scales and positions where
nothing was detected), the solution is found by minimization of
the
projection operator in the subspace of the detected coefficients
(i.e. having set to zero all coefficients at scales and positions where
nothing was detected), the solution is found by minimization of
Copyright The European Southern Observatory (ESO)