- ... LEDA
![[*]](/icons/foot_motif.gif)
- http://leda.univ-lyon1.fr
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pixels
![[*]](/icons/foot_motif.gif)
- Note that all
along this paper the optical densities are defined according to the DSS documentation as
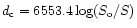 ,
where
,
where 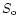 is the intensity of light transmission through an
unexposed part of the plate and S is the transmitted intensity through the considered exposed part.
We frequently use the term of pixel "intensity" for
is the intensity of light transmission through an
unexposed part of the plate and S is the transmitted intensity through the considered exposed part.
We frequently use the term of pixel "intensity" for 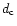 instead of the proper term of pixel
optical "density" which could lead to a confusion with the density in the sense of number of pixels per
area unit.
instead of the proper term of pixel
optical "density" which could lead to a confusion with the density in the sense of number of pixels per
area unit.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 pixels
pixels![[*]](/icons/foot_motif.gif)
- Except for the last row which is
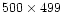 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...

![[*]](/icons/foot_motif.gif)
- The completeness curve
expressed in apparent magnitude m can be written similarly
as:
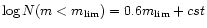 .
We will use this form in Sect. 5.4
when apparent magnitudes will be calibrated. It was used by
Hubble (1934). A
demonstration is given, e.g., by
Zwicky (1957).
.
We will use this form in Sect. 5.4
when apparent magnitudes will be calibrated. It was used by
Hubble (1934). A
demonstration is given, e.g., by
Zwicky (1957).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function
![[*]](/icons/foot_motif.gif)
- The choice of a sigmoid function is justified by the fact that we
are looking for a bimodal answer. Note that this sigmoid function is not applied on inputs Pi which are
not considered as neurones.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.