4 Reddening and temperature determination

In order to discriminate between stars having different reddening and temperature characteristics, a combination of colour indices must be found such that temperature tracks (i.e. curves of constant reddening) do not cross each other in the related colour diagram. In the XMM-OM photometric system, we found only one fully suitable pair of such colour indices: (u-uvw1) and (b-v). The corresponding colour diagram is shown in Fig. 4. This figure is representative of the weakest reddenings, but the diagram keeps its properties up to $A_V \sim 13$. Only a slight adaptation of the lowest temperature bound (9000 K  $\rightarrow 11000$ K) is necessary. We did not plot stars below 9000 K in Fig. 4 because the temperature tracks of MS stars begin to overlay at this temperature, so that nothing can be said for lower temperatures. Uncertainties on the photometry will anyhow probably hamper any temperature determination below 10000 K (a 0.05 mag photometric error can bring any 10000 K star on the 9000 K star locus). Above that value, the precision on the temperature determination depends on the temperature itself, but is typically of a few thousand Kelvins for colour indices accurate to 0.05 mag and for stars in the middle of the temperature domain. Such accuracy allows a reddening determination with a precision of about $\sim$0.3 magnitudes in A_V at any but the "coolest'' temperatures (< 11000 K).

The situation is slightly worse when one includes giant stars as well since the temperature tracks for the giants at a given reddening cross those of the less reddened MS stars. Even worse, they pass below the locus of the 9000 K MS stars at $\sim$10500 K. As any place below this line can be occupied by stars with various combinations of temperature and reddening, the domain in which a temperature determination is possible for giants is restricted to stars above $\sim11000$ K. As one does not know a priori whether or not a star is a giant, this of course also sheds some uncertainty on the temperature and reddening determination for MS stars below $\sim12-13000$ K, where temperature tracks for MS stars and giants begin to significantly differ from each other.

Figure 6: a) The (u-b) vs. (b-v) colour diagram for MS stars reddened according to Cardelli et al. (1989) reddening law with RV=3.1 (filled circles) and RV=5.5 (open circles). Each temperature track runs from 9000 K (bottom) to 35000 K (top). The reddening runs from AV=0. (leftmost track) to AV=4.0 (rightmost track). The additional diamond symbol points to the star with $T_{\rm eff}~=~15000$ K, AV=2. and RV=5.5 (see text). b) The (u-uvw1) vs. (b-v) colour diagram with the same conventions

Other discriminant colour indices than those of Fig. 4 exist in the system, but their combination with other ones only allows to determine the temperature and the reddening of the observed stars on much more restricted ranges of reddening and/or temperature. One can nevertheless design another, independent, reddening determination technique. In Fig. 4, reddening and temperature influence both colour indices plotted on the axes. As we will see now, one can nearly decouple these parameters and obtain better precision on the reddening. To do so, we need to define a colour index that is independent of reddening and another that is proportional to it. The former, that we will call $ic_{\rm0}$, is defined as

$$ic_{\rm0} = (uvw2-uvw1) - \frac{E(uvw2-uvw1)}{E({u-uvw1)}} (u-uvw1)$$

where E(x-y) stands for the colour excess of the (x-y) colour index. ic₀ will remain a reddening free colour index as long as the colour excess ratio remains constant. This property is verified for stars with $T_{\rm eff}\geq 9\,000$ K and $A_V\leq 5.5$. Nevertheless, since $A_{\rm 2000}~\sim~3~A_V$, four magnitudes of absorption in V correspond to more than ten magnitudes of absorption in the uvm2 and uvw2 filters. Hence, from now on, we will only consider the $A_V~\leq~4$ domain. The mean E(uvw2-uvw1)/E(u-uvw1) colour excess ratio over this range is -2.83 ($\pm\,0.27$). It is worth to note that (uvw2-uvw1) and (u-uvw1) are, with (u-b) and (b-v), the only pairs of colour indices allowing the definition of a reddening free index over a reasonable range of stellar parameters.

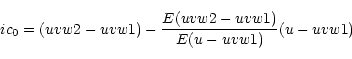
In order to define the reddening dependent index, that we will call $ic_{\rm red}$, the most obvious choice is the empirical

$$ic_{\rm red}~=~uvm2~-~(uvw1~+~uvw2)\,/\,2.$$

This index could be used but it is not really independent from $ic_{\rm0}$ and its reddening dependence can be ameliorated. Indeed, though the uvm2 filter stands on the 2175 Å absorption bump, the uvw1 and uvw2 filters are not symmetric with respect to it, and of more importance, the uvw2 filter is significantly affected by the 2175 Å absorption bump too. To refine the choice, we explored a large number of UV magnitude combinations and were finally brought to the conclusion that the best choice in terms of simplicity and dynamics of the index (and hence in terms of accuracy) is

$$ic_{\rm red}~=~uvm2~-~uvw1.$$

There is in fact a wide variety of reddening-dependent indices in the XMM-OM system and, to give just another very simple one, (uvw2-uvw1) is nearly as good as (uvm2-uvw1). Even (b-v) could be used as reddening-dependent index, so that the whole treatment that we carry on here on the UV filters could be performed on the ubv filters as well. Nevertheless, it is important to note that, although the reddening-free index based on the optical filters is much better than the one based on the ultraviolet filters ( $E(u-b)/E(b-v)~=~0.80~\pm~0.02$; compare the error bar with the UV case), the dynamic of the (b-v) index is smaller than the one of the (uvm2-uvw1) index. Consequently, at equivalent accuracy on the photometry, the reddening determined thanks to the UV filters will be more accurate than the one obtained on the basis of the optical photometry (except for temperatures lower than 10000 K or higher than 25000 K). If UV and optical photometries are available, reddening determinations in both domains should of course be used as a quality check. Indeed, as we will see in Sect. 5, the simultaneous use of visible and UV data allows a control of the consistency of the adopted reddening law.

Although lots of reddening dependent indices exist, none is perfectly independent from temperature and from $ic_{\rm0}$ so that no simple $A_V=A_V(ic_{\rm red})$ relation can be drawn. Instead, one has to perform a bi-dimensional fit over the ( $ic_{\rm0}$, $ic_{\rm red}$) plane (Fig. 5a) to get the $A_V=A_V(ic_{\rm0},~ic_{\rm red})$ relation. We do not present this fit here since its detailed analytical form can only be usefully obtained through actual in-orbit satellite calibrations. The reddening dependency of $ic_{\rm red}$ is illustrated in Figs. 5a and 5b. The solid line in Fig. 5b represents a section of the colour diagram shown in Fig. 5a at $ic_{\rm0}~=~0.6$.

This reddening determination method, based on a reddening free and a reddening dependent index, is more accurate than what can be expected with the procedure outlined in Fig. 4 since error bars of 0.2 and 0.05 mag on $ic_{\rm0}$ and $ic_{\rm red}$ respectively lead to $\leq~0.15$ mag uncertainty on A_V. On the other hand, one can see by comparing Fig. 5a and Fig. 4 that the uncertainties on A_V, due to the fact that the temperature tracks for MS and giant stars diverge at the coolest temperatures in the (u-uvw1) vs. (b-v) colour diagram, are partly removed here for the weakest reddenings. Nevertheless, the colour diagram shown in Fig. 4 remains necessary since the $A_V=A_V(ic_{\rm 0},ic_{\rm red})$ fit is not valid for all temperatures, so that we need an independent determination of temperature, precisely allowed by Fig. 4.