

Up: The Henize sample of
Subsections
3 Geneva photometry
The Henize sample of S stars has been monitored in the Geneva photometric
system on the Swiss telescope at La Silla (Chile). Detailed information
on this photometric system and on the data reduction can be found in
Golay (1980), Rufener (1988) and
Rufener & Nicolet (1988).
Among the 205 S stars of the Henize sample, 179 could
be reached with the 70 cm Swiss telescope,
with an average of 4 good-quality photometric measurements
(in all filters) per star.
Some photometric measurements have been discarded. They concern mostly
misclassified stars, or stars with abnormal
colours:
- Misclassified stars:
Hen 22 and 154 are two stars misclassified as S, as revealed by
low-resolution spectra (Van Eck & Jorissen 1999, hereafter Paper I; see also Paper III).
Hen 22 is a mid-K giant (
 K3-5) and Hen 154 a late-G giant (
K3-5) and Hen 154 a late-G giant ( G8);
G8);
- Single measurement revealing abnormally blue colours:
Only a single very blue measurement (U-B=2.26; B-V=0.48) is available for Hen 82;
a nearby field main-sequence star could well have been measured instead of the
faint and variable S star Hen 82.
In fact, the S star Hen 82 is most probably a Mira
(strong H
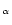 and H
and H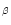 emission are visible on its
low-resolution spectrum; spectral type S5,8 according to Henize
(as listed in Stephenson 1984).
Although Mira stars are known to sometimes exhibit such blue colours,
Hen 82 has been removed from the photometric data set, given the lack of
additional photometry confirming the blue colours
of this star.
The same holds true for Hen 181 (=V407 Sco; U-B=2.17; B-V=-0.53);
emission are visible on its
low-resolution spectrum; spectral type S5,8 according to Henize
(as listed in Stephenson 1984).
Although Mira stars are known to sometimes exhibit such blue colours,
Hen 82 has been removed from the photometric data set, given the lack of
additional photometry confirming the blue colours
of this star.
The same holds true for Hen 181 (=V407 Sco; U-B=2.17; B-V=-0.53);
- Close visual binaries:
Several stars (Hen 47, 94, 105, 155)
were found to be close visual binaries, and their photometric data have
therefore not been considered for the cluster analysis presented in Paper III.
In all these cases, two spectra separated by less than 10'' (angular
separation on the sky projected on the direction perpendicular to the
slit, corresponding
to less than 15 pixels on the CCD frame) have been recorded by the
Boller & Chivens spectrograph (Sect. 7).
Rough estimates of the companion spectral type could be obtained in
all cases, but Hen 94 which is too faint:
Hen 47 (>5''): S + K4V; Hen 105 (>4''): S + late BV or early AV;
Hen 155 (>14''): S + G5 IV-III.
The numbers in parentheses provide a lower limit on the angular
separation.
Hen 47 is the only one among those cases where the physical association between
the two stars is clearly unlikely. The difference in absolute visual magnitudes
between the S star and a K4V star is at least 7 magnitudes, but the observed
difference in apparent visual magnitudes is less extreme, since the available
photometry clearly reveals composite colours.
All these pairs lie within 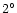 of the galactic
plane (except Hen 155 with
of the galactic
plane (except Hen 155 with
 )
where crowding may be
severe. If some of these pairs would nevertheless turn out to be physical,
the less evolved main sequence companion would allow to set a lower
limit on the mass of the S star, namely >3
)
where crowding may be
severe. If some of these pairs would nevertheless turn out to be physical,
the less evolved main sequence companion would allow to set a lower
limit on the mass of the S star, namely >3
 for Hen 105.
These masses are compatible with S stars being
intermediate-mass stars;
for Hen 105.
These masses are compatible with S stars being
intermediate-mass stars;
- Magnitudes fainter than 16.5:
All magnitudes fainter than 16.5 were rejected, as well
as their associated standard deviations, because at
such faint magnitudes the flux contribution from the sky is dominating.
For our S stars, magnitudes fainter than 16.5
only occur in the U filter, except for Hen 122 (B = 17.82),
which is flagged in Table 4.
The stars having U>16.5 fall in two categories:
(i) either the star has some of its U measurements
fainter than U=16.5;
in that case only the measurements brighter than U=16.5 were considered;
(ii) the star has all its U measurements fainter than U=16.5;
no U standard deviation is computed in that case.
The column labelled nU in Table 4 indicates the number of
measurements fainter than U=16.5.
The average magnitudes were computed from the weighted fluxes
according to Eq. (2) of Rufener (1988), where the weights
refer to the quality of the measurements.
The reduced standard deviation
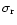 is computed by quadratically
subtracting the instrumental error
is computed by quadratically
subtracting the instrumental error 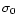 from the standard deviation
from the standard deviation
 .
The instrumental error is computed by interpolating Fig. 2 of
Barblan et al. (1998), giving the mean precision as a function of the
magnitude for observations performed in the Geneva system.
If
.
The instrumental error is computed by interpolating Fig. 2 of
Barblan et al. (1998), giving the mean precision as a function of the
magnitude for observations performed in the Geneva system.
If
 ,
then
,
then
 .
The reduced standard deviation has not been computed for magnitudes
fainter than 16.5, because of the large uncertainties
affecting the mean precision
.
The reduced standard deviation has not been computed for magnitudes
fainter than 16.5, because of the large uncertainties
affecting the mean precision 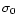 at such faint magnitudes.
at such faint magnitudes.
3.3 Dereddening
Each star has been dereddened according to the following procedure:
(i) If
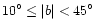 ,
the colour excess EB-Vis taken from Burstein & Heiles (1982) and
is multiplied by the factor
,
the colour excess EB-Vis taken from Burstein & Heiles (1982) and
is multiplied by the factor
![$[1- \exp(-10~r~\sin\vert b\vert)]$](/articles/aas/full/2000/13/h1905/img23.gif) ,
where r is the
distance in kpc and b is the galactic latitude (Feast et al. 1990);
72 stars are concerned.
The visual extinction is then
computed with
,
where r is the
distance in kpc and b is the galactic latitude (Feast et al. 1990);
72 stars are concerned.
The visual extinction is then
computed with
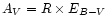 ,
where R=3.1.
,
where R=3.1.
(ii) If
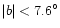 ,
AV(r) is taken from
Neckel & Klare (1980); 70 stars are concerned.
,
AV(r) is taken from
Neckel & Klare (1980); 70 stars are concerned.
(iii) If
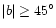 ,
or if the star is not
on the Milky Way fields defined by Neckel & Klare (1980),
or if it falls outside their AV(r) diagram
(i.e., if the star is located too far away), then the
visual extinction is taken from Arenou et al. (1992);
37 stars are concerned.
,
or if the star is not
on the Milky Way fields defined by Neckel & Klare (1980),
or if it falls outside their AV(r) diagram
(i.e., if the star is located too far away), then the
visual extinction is taken from Arenou et al. (1992);
37 stars are concerned.
The dereddening procedure then requires to
assign absolute visual magnitudes
to S stars. From HIPPARCOS parallaxes, intrinsic S stars
are known to be brighter than extrinsic S stars (Van Eck et al. 1998),
but several factors (intrinsic variability, as well as the Lutz-Kelker
bias) prevent from giving accurate average luminosities
for both classes of S stars.
The only previous large-scale estimate of absolute visual magnitudes
of S stars is by Yorka & Wing (1979), who
derived that the average MV at maximum light is of the order
-1.5 to -2.0 for Mira S stars (i.e., intrinsic S stars)
and -1 for non-Mira S stars (presumably mostly extrinsic S stars).
In principle intrinsic S stars and extrinsic S stars should thus be
assigned different absolute magnitudes (say MV=-1 for extrinsic S stars
and MV=-2 for intrinsic S stars), depending on whether
they have technetium or not.
This approach has not been retained here since
(i) the only unambiguous way to distinguish extrinsic from intrinsic
S stars is technetium detection, and this information is available
only for 70 S stars (out of 205); the other parameters
capable of segregating the two kinds of S stars have only a statistical
efficiency (see the discussion about Sb in Paper III),
and (ii) this would introduce an a priori distinction
between extrinsic and intrinsic S stars, which would then be difficult
to disentangle from possible genuine photometric differences derived
subsequently.
While the intrinsic S stars
are brighter than the extrinsic ones, they are also much redder,
hence their V magnitude is dimmed.
Therefore the single plausible value of MV=-1 has been assigned,
for dereddening purposes only, to both extrinsic and intrinsic S stars.
The dereddening process is iterated until convergence of the apparent
V magnitude is achieved (to a level of 10-4 mag).
The dereddened U and B magnitudes are then computed, using
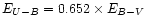 ,
a relation derived by
Cramer (1994) for B stars in the Geneva photometric system
(no such relation is available for late-type stars).
,
a relation derived by
Cramer (1994) for B stars in the Geneva photometric system
(no such relation is available for late-type stars).


Up: The Henize sample of
Copyright The European Southern Observatory (ESO)
![]() of the galactic
plane (except Hen 155 with
of the galactic
plane (except Hen 155 with
![]() )
where crowding may be
severe. If some of these pairs would nevertheless turn out to be physical,
the less evolved main sequence companion would allow to set a lower
limit on the mass of the S star, namely >3
)
where crowding may be
severe. If some of these pairs would nevertheless turn out to be physical,
the less evolved main sequence companion would allow to set a lower
limit on the mass of the S star, namely >3
![]() for Hen 105.
These masses are compatible with S stars being
intermediate-mass stars;
for Hen 105.
These masses are compatible with S stars being
intermediate-mass stars;