8 Structural parameters

For a subsample ( I₈₁₄<26) we computed size, surface brightness, light concentration index, asymmetry index.

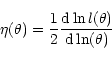
The measure of the size of distant galaxies needs the use of a metric radius, that is a size independent on the redshift and light profile. We estimated a metric radius based on the Petrosian function (Petrosian 1976), defined (Kron 1995) as

$$\eta(\theta)=\frac{1}{2}\frac{{\rm d}\ln l(\theta)}{{\rm d} \ln(\theta)}$$

where $l(\theta)$ is the light growth curve. This function has the property:

$$\eta(\theta)=\frac{I(\theta)}{<I>_{\theta}}$$

where $I(\theta)$ is the surface brightness at the radius $\theta$ and $<I>_{\theta}$ is the mean surface brightness within $\theta$. We defined for each galaxy the angular size as the value of $\theta_{0.5}$ such that $\eta(\theta)=0.5$ (Bershady et al. 1998; Saracco et al. 2000). In order to determine the function $\eta(\theta)$ we obtained the intensity profile, through multi-aperture photometry at equispaced (0.04 pixel) diameters, and subsequently interpolated it by a spline fit. There are sources whose $\eta(\theta)$ is always larger than 0.5 (considering as a border the aperture i-th such that mag_i+1> mag_i); in these cases we defined $\theta_{0.5}=-1$, and also all quantities linked to $\theta_{0.5}$ were arbitrarily set -1. We also measured the effective radius (half-light radius, $r_{{\rm eff}}$); for I₈₁₄<26 the relation $\theta$ vs. $r_{{\rm eff}}$ is well fitted by $\theta_{0.5}=1.2r_{{\rm eff}}$. After determining $\theta_{0.5}$, we computed for each galaxy the mean surface brightness within $\theta_{0.5}$.

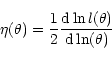
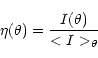
Abraham et al. (1994) and Abraham et al. (1996) showed that two indexes, namely an asymmetry index (A) and a central concentration index ( $C_{{\rm abr}}$), are very useful in order to estimate a quantitative galaxy morphology. The former is determined by rotating the galaxy by 180$^\circ$ and subtracting the resulting image from the original one. The asymmetry index is given by the sum of absolute values of the pixels in the residual image, normalized by the sum of the absolute value of the pixels in the original image and corrected for the intrinsic asymmetry of the background. The concentration index is given by the ratio of fluxes in two isophotes, based on the analysis of light profiles. The measure of these indexes is independent of colour, though they correlate well with optical colours.

We therefore computed both the asymmetry and the concentration indexes following Abraham et al. (1994) and Abraham et al. (1996), but also computed a different light concentration parameters.

That is we computed

$$C_\eta=\frac{F(<\theta_{0.5})}{F(<1.5\theta_{0.5})}$$

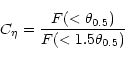
(Saracco et al. 2000), i.e. the ratio between the flux within radius $\theta_{0.5}$ and the flux within $1.5\theta_{0.5}$.

As discussed by Saracco et al. (1999), $C_\eta$ is independent from the redshift of the source, since it is related to a metric size and is independent of the asymptotic profile. Brinchmann et al. (1998) on the contrary pointed out that the central concentration $C_{{\rm abr}}$defined by Abraham et al. (1994, 1996) is redshift-dependent. $C_{{\rm abr}}$ has been computed in order to classify our galaxies and compare our results with HDF-North. We tested the various parameters against apparent magnitude and checked any correlation with colours (Conselice et al. 2000). We selected two subsamples, composed respectively by galaxies with both B₄₅₀-V₆₀₆ and V₆₀₆-I₈₁₄ redder or bluer than a local elliptical or a local irregular galaxy. We used these subsamples as tracers of colours.

FLUX-ISO	FLUXERR-ISO	MAG-ISO	MAGERR-ISO	MTOT	MTOT-ERR	ISOAREA-IMAGE
0.354	0.0012	23.21	0.0037	23.17	0.1	1027
0.037	7.9E-4	25.64	0.022	25.61	0.1	338
0.024	4.3E-4	26.11	0.019	25.81	0.1	139
0.111	7.8E-4	24.47	0.007	24.32	0.1	470
0.035	6.2E-4	25.70	0.019	25.47	0.1	279
0.027	5.7E-4	25.99	0.023	25.78	0.1	236
0.125	8.0E-4	24.34	0.007	24.20	0.1	507

X-IMAGE	Y-IMAGE	ALPHA-J2000	DELTA-J2000	X2-IMAGE	Y2-IMAGE	ERRX2-IMAGE
270.59	1900.766	338.272981	-60.555908	47.9	25.41	0.0016
290.17	1569.351	338.272480	-60.559576	44.6	29.47	0.0252
304.80	1706.001	338.272175	-60.558062	8.2	11.51	0.0044
321.70	1995.368	338.271847	-60.554856	26.4	20.98	0.0023
372.10	1877.157	338.270679	-60.556161	27.9	15.58	0.0189
375.62	717.7169	338.270398	-60.568997	31.6	20.41	0.0026

ERRY2-IMAGE	A-IMAGE	B-IMAGE	ERRA-IMAGE	ERRB-IMAGE	FLAGS	CLASS-STAR
7.9E-4	7.08	4.81	0.041	0.02672239	0	0.91
0.018	6.69	5.40	0.15	0.1358412	2	2.2E-4
0.006	3.44	2.81	0.079	0.06579173	0	0.02
0.001	5.33	4.35	0.05	0.04017934	0	0.02
0.010	5.34	3.87	0.14	0.09491127	0	3.0E-4
0.0015	5.63	4.50	0.05	0.03895507	0	0.02

SN	B-V	THETA	MUTHETA	CM	C-ABR
133.95	0.53	0.1489	21.11	0.7708	0.663
25.60	0.43	0.4587	25.5	0.7479	0.211
25.55	-0.07	0.1899	24.12	0.7705	0.321
62.89	0.52	0.2793	23.38	0.7606	0.359
22.07	0.67	0.3213	25.08	0.7711	0.157
68.09	0.10	0.3192	23.46	0.7829	0.352

The asymmetry index (Fig. 9) seems not to be biased: the faintest sources are on the whole more symmetric than brighter ones, but the presence of asymmetric objects also in the last bins suggest this feature to be linked to the nature of these galaxies. The trend towards high symmetry may be due to the influence of noise, which makes the profile smoother.

The central concentration index $C_{{\rm abr}}$ defined by Abraham et al. (1994, 1996) seems to be biased against compact sources at faint magnitudes ( I₈₁₄>24.5), while $C_\eta$ does not correlate with apparent magnitude (Figs. 10-11).