

Up: A catalogueof galaxies
Completeness correction for faint undetected sources strongly depends on
the source apparent spatial structure besides to their magnitude. To estimate completeness
via simulations we must account for sub-galactic structures. These could be quite common at
high redshift and detectable by HST, and for the morphology which is that of the co-moving UV
and B pass-bands and hence is strongly affected by star formation episodes. These features
imply that "typical'' profiles of galaxies are not able to well describe the shapes of a
lot of galaxies in the HDF-S. Thus, in order to reproduce the manifold of shapes which
characterizes sources in the HDF-S we generated a set of simulated frames by directly
dimming the original frames themselves by various factors while keeping constant the RMS
(Saracco et al. 2000). This procedure has allowed us to avoid any assumption on the
source profile while providing an artificial fair dimmed sample in a real background noise.
We thus define the correction factor 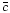 as the mean number of dimmed galaxies which
should enter the fainter magnitude bin over the mean number of detected ones. It represents
the inverse of the fraction of galaxies undetected in each bin. If ni is the number of
galaxies detected in the i-th bin of the original catalogue and mi+1 is the number of
sources in the i+1-th bin of the simulated catalogue, the correction factor
as the mean number of dimmed galaxies which
should enter the fainter magnitude bin over the mean number of detected ones. It represents
the inverse of the fraction of galaxies undetected in each bin. If ni is the number of
galaxies detected in the i-th bin of the original catalogue and mi+1 is the number of
sources in the i+1-th bin of the simulated catalogue, the correction factor
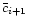 corresponding to the ratio between the expected number of galaxies (ni) and the number of
galaxies recovered (mi+1). The "true'' number of galaxies in the i+1-th bin of the
original catalogue is then Ni+1=
corresponding to the ratio between the expected number of galaxies (ni) and the number of
galaxies recovered (mi+1). The "true'' number of galaxies in the i+1-th bin of the
original catalogue is then Ni+1=
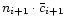 ,
where
,
where 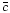 is the
mean over different simulations for the same frame.
is the
mean over different simulations for the same frame.
When dimming fluxes by a factor
F=100.4y, magnitudes are y mag fainter, but also noise
is lowered: if 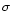 is the sky RMS on original images, the dimmed frames have a RMS of
is the sky RMS on original images, the dimmed frames have a RMS of
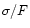 .
We then added a frame of pure Poissonian noise, with a sky RMS
.
We then added a frame of pure Poissonian noise, with a sky RMS
The final
images have, by construction, the correct RMS. By choosing y=0.5 mag, the artificial noise
added is
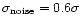 ,
i.e. about one third of the final image is due to pure
Poissonian noise. As showed in Figs. 5-6 and in Table 4, this choice allowed us to correct
up to
V606=29, with brighter limits in the other bands.
,
i.e. about one third of the final image is due to pure
Poissonian noise. As showed in Figs. 5-6 and in Table 4, this choice allowed us to correct
up to
V606=29, with brighter limits in the other bands.
We tried also y=1 mag, but the estimated incompleteness was catastrophic, corresponding to
96%. This result seemed caused by the high simulated noise (
 =0.84
=0.84
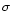 ,
i.e. almost one half of noise is artificial), which caused also brighter bins to be
incomplete.
,
i.e. almost one half of noise is artificial), which caused also brighter bins to be
incomplete.
The completeness correction allowed the computation of differential number counts up to
fainter magnitudes: we thus determined the slopes of the number counts relation. Our best fit
gives
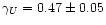 ,
,
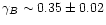 ,
,
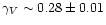 and
and
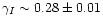 (see Volonteri et al. 2000, for a detailed discussion).
(see Volonteri et al. 2000, for a detailed discussion).
Table 4:
Correction factor 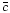 and error. The factor
and error. The factor 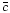 accounts for the
galaxies missed in the detection due to the influence of noise. The "true'' (corrected)
number of galaxies in each bin is
accounts for the
galaxies missed in the detection due to the influence of noise. The "true'' (corrected)
number of galaxies in each bin is 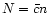 ,
where n is the raw number of detections
,
where n is the raw number of detections
| Filter |
mag |
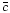 |
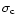 |
| F300W |
26.75 |
2.12 |
0.07 |
| F450W |
27.25 |
1.11 |
0.05 |
| |
27.75 |
1.56 |
0.04 |
| |
28.25 |
3.25 |
0.11 |
| F606W |
28.25 |
1.34 |
0.02 |
| |
28.75 |
2.67 |
0.1 |
| F814W |
27.25 |
1.09 |
0.04 |
| |
27.75 |
1.81 |
0.11 |
| F110W |
27.25 |
1.24 |
0.14 |
| |
27.75 |
2.56 |
0.19 |
| F160W |
27.25 |
1.93 |
0.42 |
| F222M |
24.25 |
4.09 |
1.23 |
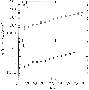 |
Figure 5:
V606 and I814 number counts: raw counts are shown with
empty symbols, corrected counts with filled symbols |
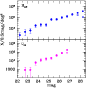 |
Figure 6:
B450 and U300 number counts: raw counts are shown with empty symbols,
corrected counts with filled symbols |


Up: A catalogueof galaxies
Copyright The European Southern Observatory (ESO)
![]() is the sky RMS on original images, the dimmed frames have a RMS of
is the sky RMS on original images, the dimmed frames have a RMS of
![]() .
We then added a frame of pure Poissonian noise, with a sky RMS
.
We then added a frame of pure Poissonian noise, with a sky RMS
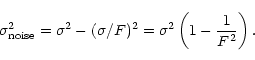
![]() =0.84
=0.84
![]() ,
i.e. almost one half of noise is artificial), which caused also brighter bins to be
incomplete.
,
i.e. almost one half of noise is artificial), which caused also brighter bins to be
incomplete.
![]() ,
,
![]() ,
,
![]() and
and
![]() (see Volonteri et al. 2000, for a detailed discussion).
(see Volonteri et al. 2000, for a detailed discussion).

