"Pseudo-total'' magnitudes were therefore estimated using the method of Djorgovski et al. (1995) and Smail et al. (1995): they assigned the isophotal magnitude to sources with isophotal diameter larger than $\theta_1\approx2-3$ FWHM, while smaller sources are assigned an aperture corrected magnitude, that is the magnitude within an aperture $\theta _1$ corrected to the magnitude within $\theta _2$ , larger than $\theta _1$ : $m=m(\theta1)+\Delta m$ , $\Delta m=~<m(\theta2)-m(\theta1)>$ . In literature the choice of $\theta _1$ and $\theta _2$ is based on multiples of the FWHM of images. In the HDF-S the excellent seeing needs a different approach, we therefore estimated magnitudes for our sample on the basis of the following steps:

$\theta _1$ has been defined as the minimum apparent diameter of a galaxy having an effective diameter $r_{\rm e}=10$ Kpc. Hereafter we use a $\Lambda=0$ cosmology, with q₀=0.5 and H₀=50 km s^-1 Mpc^-1 unless differently specified. With this choice $\theta_1=1.2$ arcsec. Since the correction $\Delta m$ is measured on a subsample of relatively bright galaxies, we defined an area for each band, A₉₀, such that 90 $\%$ of galaxies belonging to the djorg subsample has isophotal area smaller than A₉₀. $\theta _2$ is defined as the diameter corresponding to a circle of area A₉₀.

At bright magnitudes Kron's technique, based on an adaptive aperture, $r_{1}=\frac{\sum rI(r)} {\sum I(r)}$ , gives very good results. Kron (1980) and Bertin & Arnouts (1996) demonstrated that a photometry within an adaptive aperture (2.5r₁) is expected to measure a fraction of the total flux between 0.9 and 0.94. We then chose to use Kron's magnitude ( $m_{{\rm kr}}$ ) as a reference in order to test our method: if the flux fraction measured by Kron's technique is 0.94, the fraction estimated by our "pseudo-total'' magnitude ( $m_{{\rm dj}}$ ) is $x=0.94~10^{0.4(m_{{\rm kr}}-m_{{\rm dj}})}$ . Our procedure is intended to correct the systematic underestimate ( $6-10\%$ ) of total flux typical of Kron's technique, which may be important for very faint sources.

Table 1 and Fig. 1 show clearly that statistically $\Delta m$ corrects for the flux underestimate typical of Kron's magnitudes. Moreover our estimate of total magnitudes has a narrower distribution at low S/N than Kron magnitude, see Fig. 3, and in a plot magnitude-isophotal area (Fig. 2) it is not evident any discontinuity in the passage between large and small sources (i.e. sources with $\theta >\theta _1$ or vice versa). This test confirms the validity of our choice of $\theta _1$ .

If not differently specified, magnitudes are expressed in the AB system, that is a system based on a spectrum which is flat in $f_\nu$ : $m = -2.5 \log f_\nu -48.60$ (Oke 1974).

Table 1: Residuals $m_{{\rm kr}}-m_{\rm dj}$ vs. $m_{{\rm kr}}$ for the V₆₀₆ selected sample, if $\theta _1=1.20$ arcsec and $\theta _2$ defined as a function of A₉₀

Filter	$\theta _2$ (arcsec)	$\Delta m$	med( $m_{{\rm kr}}-m_{\rm dj}$ )	x
F300W	1.59	0.132	0.08 $\pm$ 0.40	1.01
F450W	1.85	0.163	0.11 $\pm$ 0.15	1.04
F606W	2.15	0.080	0.06 $\pm$ 0.10	0.99
F814W	2.01	0.145	0.12 $\pm$ 0.12	1.05

$\begin{figure}{\psfig{figure=ds1871f1.ps,height=80mm} } \end{figure}$

Figure 1: Residuals $m_{{\rm kr}}-m_{\rm dj}$ vs. $m_{{\rm kr}}$ for the V₆₀₆ selected sample, if $\theta _1=1.20$ arcsec, $\theta _2$ as a function of A₉₀

$\begin{figure}{\psfig{figure=ds1871f2.ps,height=80mm} } \end{figure}$

Figure 2: Plot of pseudo-total magnitude vs. isophotal area: it is not evident any discontinuity in the passage between large and small sources (i.e. sources with $\theta >\theta _1$ , corresponding to isophotal area >706 pixel²). This confirms our choice of $\theta _1$

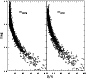$\begin{figure}{\psfig{figure=ds1871f3.ps,height=80mm} } \end{figure}$

Figure 3: Kron's magnitude and our pseudototal magnitude vs. S/N. At low S/N pseudototal magnitude has a narrower distribution than Kron's magnitude

3 Photometry