

Up: Analysis of correlations between stars
Due to the multicomponent structure of CS shells around young stars several
sources of observed polarization exist. These are: - scattering of radiation
in nonspherical disk-like dust shells; - Thomson scattering in CS gaseous
shells; - Thomson scattering in gas jets; - scattering on gas and dust
inhomogeneities rotating around a star etc.
It is important
that large IR excesses (
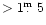 )
at 3.5
)
at 3.5 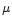 m cannot be explained by
free-free and free-bound emission. This is in good agreement with the data
for classical Be stars (most of them show near IR excesses
m cannot be explained by
free-free and free-bound emission. This is in good agreement with the data
for classical Be stars (most of them show near IR excesses
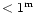 ). Thus the
main source of IR excesses in young stars is the absorption and re-emission
of radiation by dust grains. Because strong correlations between polarization
and IR colour excess E(V-L) exist for the majority of young stars we
suppose that the main source of polarization in young stars is the same as
for near IR excesses i.e. CS dust. Therefore we should not consider here the
mechanisms of polarization which are connected with CS gaseous shells. In the
framework of this assumption the observed polarization in young stars can be
described as a vector sum of several components:
). Thus the
main source of IR excesses in young stars is the absorption and re-emission
of radiation by dust grains. Because strong correlations between polarization
and IR colour excess E(V-L) exist for the majority of young stars we
suppose that the main source of polarization in young stars is the same as
for near IR excesses i.e. CS dust. Therefore we should not consider here the
mechanisms of polarization which are connected with CS gaseous shells. In the
framework of this assumption the observed polarization in young stars can be
described as a vector sum of several components:
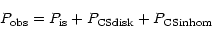 |
(5) |
where
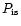 - is the interstellar component of polarization,
- is the interstellar component of polarization,
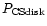 - is polarization arising in the nonspherical dust
envelope and
- is polarization arising in the nonspherical dust
envelope and
 - is polarization due to scattering CS dust
inhomogeneities. As a first step we assume that
- is polarization due to scattering CS dust
inhomogeneities. As a first step we assume that
 does not
affect strongly the value of observed polarization. Although this component
of polarization is rather small, as will be shown later, the presence of
these inhomogeneities in CS shells is an important factor that may result in
large polarimetric variations indirectly. We also exclude from our study
the interstellar component of polarization.
does not
affect strongly the value of observed polarization. Although this component
of polarization is rather small, as will be shown later, the presence of
these inhomogeneities in CS shells is an important factor that may result in
large polarimetric variations indirectly. We also exclude from our study
the interstellar component of polarization.
Grinin et al. ([1995]) in the context of the observational behaviour
of UXOrs have discussed two possibilities for the intrinsic polarization
in the framework of the dust model, namely optical dichroism of CS
nonspherical grains, and the scattering of stellar radiation in CS dust
shells. They noted that in the first case a linear dependence must be
observed between the amplitude of brightness variations and polarization
degree:
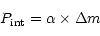 |
(6) |
where 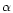 - is the factor dependent on the degree of alignment of the
dust particles in a SC cloud. In the second case, the dependence is quite
different and has the form:
- is the factor dependent on the degree of alignment of the
dust particles in a SC cloud. In the second case, the dependence is quite
different and has the form:
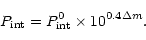 |
(7) |
As may be inferred from observations of UXOrs as well as from our analysis,
the second case is much more acceptable as an explanation for the behaviour
discussed in the present study.
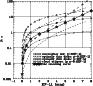 |
Figure 18:
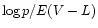 relations for different sources of polarization
relations for different sources of polarization |
In fact,
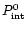 is dependent on the amount of hot dust in CS shells
and the geometry of the envelopes. Note that it is impossible to explain the
observed polarization in all young stars assuming that the dust envelopes
have a spherical shape. Therefore we will consider the disk-like envelopes.
is dependent on the amount of hot dust in CS shells
and the geometry of the envelopes. Note that it is impossible to explain the
observed polarization in all young stars assuming that the dust envelopes
have a spherical shape. Therefore we will consider the disk-like envelopes.
Let us consider two components (
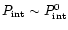 and
and
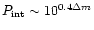 )
in Eq. (7) separately.
In the general case polarization for the disk-shaped envelope can be
described by the following formula (see Dolginov et al. [1995]):
)
in Eq. (7) separately.
In the general case polarization for the disk-shaped envelope can be
described by the following formula (see Dolginov et al. [1995]):
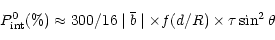 |
(8) |
where 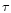 - is the optical thickness of the envelope, f(d/R) - a
function dependent on the ratio of envelope geometrical thickness to the
radius, i the inclination angle of the disks to the line of sight and
- is the optical thickness of the envelope, f(d/R) - a
function dependent on the ratio of envelope geometrical thickness to the
radius, i the inclination angle of the disks to the line of sight and
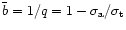 (
(
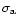 and
and
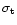 are
absorption and scattering cross-sections). Let us re-construct this formula
in terms of E(V-L). Using the canonical equations
are
absorption and scattering cross-sections). Let us re-construct this formula
in terms of E(V-L). Using the canonical equations
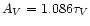 and the relation between E(B-V) and E(V-L) the optical thickness
and the relation between E(B-V) and E(V-L) the optical thickness
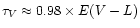 .
Thus
.
Thus
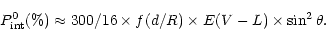 |
(9) |
Numerical values for f(d/R) are tabulated in Dolginov et al. ([1995]).
For favorable geometry and
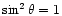
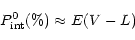 |
(10) |
or for the intermediate case
 |
(11) |
The relations (10, 11) are plotted in Fig. 18. Note that these relations
cannot explain our dependence adequately. Moreover these relations are valid
only for the optically thin case which corresponds to
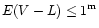 .
Note however that in the case of the presence of optically thick dust
condensations in the midplane of the envelope instead of the optically thick
narrow dust disk, the average optical thickness of this envelope may reach
the value of
.
Note however that in the case of the presence of optically thick dust
condensations in the midplane of the envelope instead of the optically thick
narrow dust disk, the average optical thickness of this envelope may reach
the value of
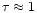 at values of
at values of
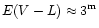 or even
larger. Incidentally, the relation (10) is in agreement with the data for
classical Be stars for which the polarization is due to the scattering
of free electrons in nonspherical optically thin disk-like CS gaseous shells.
The relations (10, 11) are also valid for some TT stars and describe well the
position of most Vega-type and post HAEBE stars. This fact is in good
agreement with the above suggestion on the presence of optically thin and
homogeneous disks around them.
or even
larger. Incidentally, the relation (10) is in agreement with the data for
classical Be stars for which the polarization is due to the scattering
of free electrons in nonspherical optically thin disk-like CS gaseous shells.
The relations (10, 11) are also valid for some TT stars and describe well the
position of most Vega-type and post HAEBE stars. This fact is in good
agreement with the above suggestion on the presence of optically thin and
homogeneous disks around them.
Let us consider now the second term of Eq. (7) assuming
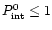 (this corresponds to the observed values for UXOrs in their
bright states).
(this corresponds to the observed values for UXOrs in their
bright states).
Because of the assumption on nonvariable IR fluxes we can re-write
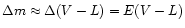 and
and
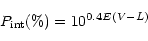 |
(12) |
or
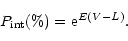 |
(13) |
This relation is also shown in Fig. 18. Note that as is evident from the
present statistical study the polarization is proportional to near IR excess
E(V-L) in the form
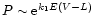 or
or
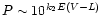 .
However the coefficient k in our relation (3) differs from those in
Eqs. (12, 13). To make the coefficients consistent we must assume that
the extinction curve for dust clouds/condensations is different from that of
the standard curve. Put another way the extinction in near IR must be
higher:
.
However the coefficient k in our relation (3) differs from those in
Eqs. (12, 13). To make the coefficients consistent we must assume that
the extinction curve for dust clouds/condensations is different from that of
the standard curve. Put another way the extinction in near IR must be
higher:
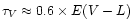 which corresponds to the ratio
which corresponds to the ratio
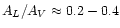 i.e. the extinction curve is flatter than the
interstellar one (see also Mitskevich [1995]). This partly nonselective
extinction can occur only due to the presence of large dust grains in clouds
from which stellar radiation is obscured. Rostopchina et al. ([1997])
noted recently that the modelling of the behaviour in UXOrs requires the
minimum size of the dust particles to be about ten times larger than that of
the interstellar matter. They have discussed this fact in terms of the growth
of particles in these kinds of objects and noted that these particles are
still smaller than in the "old" protoplanetary disks of Vega-type stars.
Simultaneous optical and IR photometry for some UXOrs which was carried out
by Hutchinson et al. ([1994]), clearly indicates the decreasing of IR
fluxes during a visual fade with the ratio that is in excellent correspondence
with
i.e. the extinction curve is flatter than the
interstellar one (see also Mitskevich [1995]). This partly nonselective
extinction can occur only due to the presence of large dust grains in clouds
from which stellar radiation is obscured. Rostopchina et al. ([1997])
noted recently that the modelling of the behaviour in UXOrs requires the
minimum size of the dust particles to be about ten times larger than that of
the interstellar matter. They have discussed this fact in terms of the growth
of particles in these kinds of objects and noted that these particles are
still smaller than in the "old" protoplanetary disks of Vega-type stars.
Simultaneous optical and IR photometry for some UXOrs which was carried out
by Hutchinson et al. ([1994]), clearly indicates the decreasing of IR
fluxes during a visual fade with the ratio that is in excellent correspondence
with
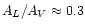 .
According to Chini et al. ([1990]) the
minimum size of the dust particles in CS shells around Vega,
.
According to Chini et al. ([1990]) the
minimum size of the dust particles in CS shells around Vega, 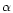 PsA and
PsA and
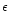 Eri is
Eri is
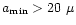 m. Similar conclusions were recently made
for HD 45677 by de Winter & van den Ancker ([1997]) who suggested that
photometric variations appeared in the star due to obscuration by CS
condensations with large (
m. Similar conclusions were recently made
for HD 45677 by de Winter & van den Ancker ([1997]) who suggested that
photometric variations appeared in the star due to obscuration by CS
condensations with large (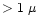 m) dust grains. Some evidence for unusually
large grains in front of some Orion stars (most of them are in our list of
post HAEBE and Vega-type stars, see Appendices 1-2) has been discussed by
Breger ([1977]) and Breger et al. ([1981]). Moreover, there is
much evidence that the wavelength dependence of polarization in most young
stars diverges considerably from that determined by the Serkowski law, namely
in the sense that polarization in the red and near IR is often higher that
might be expected for standard interstellar grains (see Tamura & Sato
[1989]; Vrba et al. [1979]; Garrison & Anderson [1978]).
m) dust grains. Some evidence for unusually
large grains in front of some Orion stars (most of them are in our list of
post HAEBE and Vega-type stars, see Appendices 1-2) has been discussed by
Breger ([1977]) and Breger et al. ([1981]). Moreover, there is
much evidence that the wavelength dependence of polarization in most young
stars diverges considerably from that determined by the Serkowski law, namely
in the sense that polarization in the red and near IR is often higher that
might be expected for standard interstellar grains (see Tamura & Sato
[1989]; Vrba et al. [1979]; Garrison & Anderson [1978]).
Taking into account the above discussion the expression for the degree of
intrinsic polarization for the majority of young stars has the form:
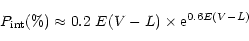 |
(14) |
for the region of
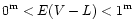 or
or
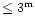 and
and
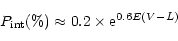 |
(15) |
for the region of
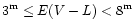 .
.
Note that the expression derived above corresponds well with the statistical
dependence (see Fig. 18). It is also important that even for optically thin
disk-like dust envelopes the polarization degree can be greater than
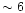 % if the stellar radiation is screened (see series of papers by
Daniel [1980a], [1980b], [1982] or
Voshchinnikov & Karjukin [1994]).
% if the stellar radiation is screened (see series of papers by
Daniel [1980a], [1980b], [1982] or
Voshchinnikov & Karjukin [1994]).
Finally, the change in the average line inclination should be caused by
multiple scattering if the optical thickness of the shell 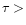 1 (this may
occur in some young stars). This leads to a decrease in the fraction of
scattering radiation and decreasing of observed polarization
(Voshchinnikov & Karjukin [1994]).
1 (this may
occur in some young stars). This leads to a decrease in the fraction of
scattering radiation and decreasing of observed polarization
(Voshchinnikov & Karjukin [1994]).
In addition note that the conclusion of the existence of large dust particles
in CS envelopes of young stars, which follows from the analysis of the
behaviour of young stars on the diagram discussed here, is beyond the reach
of classical
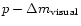 diagrams. Thus, the diagram discussed
here is more informative.
diagrams. Thus, the diagram discussed
here is more informative.


Up: Analysis of correlations between stars
Copyright The European Southern Observatory (ESO)
![]() )
at 3.5
)
at 3.5 ![]() m cannot be explained by
free-free and free-bound emission. This is in good agreement with the data
for classical Be stars (most of them show near IR excesses
m cannot be explained by
free-free and free-bound emission. This is in good agreement with the data
for classical Be stars (most of them show near IR excesses
![]() ). Thus the
main source of IR excesses in young stars is the absorption and re-emission
of radiation by dust grains. Because strong correlations between polarization
and IR colour excess E(V-L) exist for the majority of young stars we
suppose that the main source of polarization in young stars is the same as
for near IR excesses i.e. CS dust. Therefore we should not consider here the
mechanisms of polarization which are connected with CS gaseous shells. In the
framework of this assumption the observed polarization in young stars can be
described as a vector sum of several components:
). Thus the
main source of IR excesses in young stars is the absorption and re-emission
of radiation by dust grains. Because strong correlations between polarization
and IR colour excess E(V-L) exist for the majority of young stars we
suppose that the main source of polarization in young stars is the same as
for near IR excesses i.e. CS dust. Therefore we should not consider here the
mechanisms of polarization which are connected with CS gaseous shells. In the
framework of this assumption the observed polarization in young stars can be
described as a vector sum of several components:
![]() is dependent on the amount of hot dust in CS shells
and the geometry of the envelopes. Note that it is impossible to explain the
observed polarization in all young stars assuming that the dust envelopes
have a spherical shape. Therefore we will consider the disk-like envelopes.
is dependent on the amount of hot dust in CS shells
and the geometry of the envelopes. Note that it is impossible to explain the
observed polarization in all young stars assuming that the dust envelopes
have a spherical shape. Therefore we will consider the disk-like envelopes.
![]() and
and
![]() )
in Eq. (7) separately.
In the general case polarization for the disk-shaped envelope can be
described by the following formula (see Dolginov et al. [1995]):
)
in Eq. (7) separately.
In the general case polarization for the disk-shaped envelope can be
described by the following formula (see Dolginov et al. [1995]):
![]() (this corresponds to the observed values for UXOrs in their
bright states).
(this corresponds to the observed values for UXOrs in their
bright states).
![]() and
and
![]() % if the stellar radiation is screened (see series of papers by
Daniel [1980a], [1980b], [1982] or
Voshchinnikov & Karjukin [1994]).
% if the stellar radiation is screened (see series of papers by
Daniel [1980a], [1980b], [1982] or
Voshchinnikov & Karjukin [1994]).
![]() 1 (this may
occur in some young stars). This leads to a decrease in the fraction of
scattering radiation and decreasing of observed polarization
(Voshchinnikov & Karjukin [1994]).
1 (this may
occur in some young stars). This leads to a decrease in the fraction of
scattering radiation and decreasing of observed polarization
(Voshchinnikov & Karjukin [1994]).
![]() diagrams. Thus, the diagram discussed
here is more informative.
diagrams. Thus, the diagram discussed
here is more informative.