 |
Figure 13:
|
The main critical comment to the first paper of Yudin ([1988]) was
that in the case of disk-like distribution of scatterers around the stars
(that is at present a general model for the observed behaviour of young stars
and many direct evidence of such geometry now exists) no linear correlations
between ![]() and IR excesses should be observed. The justification for
this suggestion is that the polarization is proportional (for optically thin
disks) to the value of
and IR excesses should be observed. The justification for
this suggestion is that the polarization is proportional (for optically thin
disks) to the value of
![]() where i is an inclination angle of
the disks to the line of sight. The referees have commented on the existence
of a "triangle diagram" rather than a linear correlation. However as follows
from Fig. 4, even the significantly larger statistics demonstrate again the
pronounced relationship between
where i is an inclination angle of
the disks to the line of sight. The referees have commented on the existence
of a "triangle diagram" rather than a linear correlation. However as follows
from Fig. 4, even the significantly larger statistics demonstrate again the
pronounced relationship between ![]() and E(V-L) for young stars.
Note however that at present we don't know which objects have exact pole-on
orientation of CS disks for the majority of young stars (maybe with a few
exceptions). Even though the
and E(V-L) for young stars.
Note however that at present we don't know which objects have exact pole-on
orientation of CS disks for the majority of young stars (maybe with a few
exceptions). Even though the ![]() value is small it is not uniquely
determined that the CS disk has a pole-on orientation while some stars may
have low rotational velocity themselves. All available data on the rotational
velocities for young stars (about 250 objects; see Appendices 1-5) allow
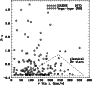
us to conclude that no correlation exists between
value is small it is not uniquely
determined that the CS disk has a pole-on orientation while some stars may
have low rotational velocity themselves. All available data on the rotational
velocities for young stars (about 250 objects; see Appendices 1-5) allow
us to conclude that no correlation exists between
![]() and
and ![]() (see Fig. 13).
(see Fig. 13).
Moreover, there is reason to believe that the compression of CS environment
takes place along the lines-of force of the interstellar magnetic field (see
for example Grinin et al. [1991] and Tamura & Sato [1989]).
For the most part the young stars are located in the plane of the Galaxy but
the orientation of interstellar magnetic field is mainly co-linear with the
direction of the axes of spiral arms. In the paper of Andriasyan & Makarov
([1989]) the directions of the Galactic coordinates for which the
orientation of interstellar magnetic field is perpendicular to the line of
sight were separated out. The correlation of these coordinates with those for
the stars in our sample shows that about 90% of the objects lie in those
regions. Thus we can reject the suggestion of pole-on orientation of CS
disks for most of the selected stars. In addition note that, even for the
pole-on orientation of the disks polarization of radiation may take
place due to the presence of the rotating dust inhomogeneities in CS shells,
or if the disks have no circular symmetry (for example for an ellipse-like
envelope and location of a star in one of the focus of this ellipse). In any
case even a small departure of i from
![]() gives an ellipse for the
projection of the disk on the sky-plane which results in the detectable
polarization of radiation (see Discussion in Yudin et al. [1999]).
Nevertheless, some influence of the disk's inclination on the observed
polarization does occur for individual stars (see for example Yudin et al.
[1999]). One can suppose that the inclination effect may be pronounced
for homogeneous and optically thin disks when the main mechanism
of polarization is the scattering in these envelopes and no other sources
of polarization exists (such as that of scattering on dust inhomogeneities
or condensations revolving around a star).
gives an ellipse for the
projection of the disk on the sky-plane which results in the detectable
polarization of radiation (see Discussion in Yudin et al. [1999]).
Nevertheless, some influence of the disk's inclination on the observed
polarization does occur for individual stars (see for example Yudin et al.
[1999]). One can suppose that the inclination effect may be pronounced
for homogeneous and optically thin disks when the main mechanism
of polarization is the scattering in these envelopes and no other sources
of polarization exists (such as that of scattering on dust inhomogeneities
or condensations revolving around a star).
We may also compare the values of intrinsic polarization and ![]() for the group of HAEBE stars with Algol-like minima (most of them have
the similar spectral types around A5). During the photometric minima
due to eclipse of nonpolarized stellar light we can detect scattered
radiation from their nonspherical dust envelopes. As can be seen in Fig. 12
there is no evidence that stars with larger values of
for the group of HAEBE stars with Algol-like minima (most of them have
the similar spectral types around A5). During the photometric minima
due to eclipse of nonpolarized stellar light we can detect scattered
radiation from their nonspherical dust envelopes. As can be seen in Fig. 12
there is no evidence that stars with larger values of ![]() show
larger values of polarization. However, at present, the list of this type of
HAEBE stars is not large enough to draw definite conclusions.
It is interesting that large Algol-like minima of brightness are observed
for some stars which have respectively small values of
show
larger values of polarization. However, at present, the list of this type of
HAEBE stars is not large enough to draw definite conclusions.
It is interesting that large Algol-like minima of brightness are observed
for some stars which have respectively small values of ![]() (60-90 km s-1). Discussion on this behaviour will be given in Sect. 7.
(60-90 km s-1). Discussion on this behaviour will be given in Sect. 7.
It is interesting to compare polarimetric and ![]() data discussed
here for young stars with those for classical Be stars. The correlation
between p and
data discussed
here for young stars with those for classical Be stars. The correlation
between p and ![]() values for classical Be stars has been investigated
by many authors. McLean & Brown ([1978]) plotted the values of pversus
values for classical Be stars has been investigated
by many authors. McLean & Brown ([1978]) plotted the values of pversus ![]() for a sample of 67 classical Be stars and found a
"triangle" distribution (see their Fig. 2).
In Fig. 14 we plot the values of polarization versus
for a sample of 67 classical Be stars and found a
"triangle" distribution (see their Fig. 2).
In Fig. 14 we plot the values of polarization versus ![]() for the
larger group of classical Be stars (285 objects).
With six times better statistics (compared with previous studies) we can
conclude that the relation shows again a "triangle" distribution but not in
the same sense as has been discussed by McLean & Brown ([1978]).
The differences are that the polarization degree has reached maximum values
for stars with intermediate values of rotational projected velocities
200 km s-1
for the
larger group of classical Be stars (285 objects).
With six times better statistics (compared with previous studies) we can
conclude that the relation shows again a "triangle" distribution but not in
the same sense as has been discussed by McLean & Brown ([1978]).
The differences are that the polarization degree has reached maximum values
for stars with intermediate values of rotational projected velocities
200 km s-1
![]() km s-1 and there are a small portion of stars
(mainly Be stars with observed polarization) with large polarization
among the stars with relatively low
(
km s-1 and there are a small portion of stars
(mainly Be stars with observed polarization) with large polarization
among the stars with relatively low
(
![]() km s-1, and very high (
km s-1, and very high (
![]() 350 km s-1, projected
rotational velocities. The detailed dicsussion of this behaviour and the
results of a statistical study of different observational characteristics
of classical Be stars may be found in Yudin ([2000]).
350 km s-1, projected
rotational velocities. The detailed dicsussion of this behaviour and the
results of a statistical study of different observational characteristics
of classical Be stars may be found in Yudin ([2000]).
The investigation of ![]() distributions was not the initial aim of the
present study. However large statistics make it possible to compare the
rotational velocity distributions for the groups of stars which are at
different stages of evolution, which may be interesting in the context of
the present work.
distributions was not the initial aim of the
present study. However large statistics make it possible to compare the
rotational velocity distributions for the groups of stars which are at
different stages of evolution, which may be interesting in the context of
the present work.
Note that Davis et al. ([1983]) have noted the difference in the
frequency distribution of ![]() between Herbig Be stars and classical Be
stars (but for a small sample). B
between Herbig Be stars and classical Be
stars (but for a small sample). B
![]() hm & Catala ([1995]) recently
compared
hm & Catala ([1995]) recently
compared ![]() values for low, intermediate and high-mass HAEBE stars
and have estimated the mean projected rotational velocities (MRPV) for 27
HAEBE stars:
values for low, intermediate and high-mass HAEBE stars
and have estimated the mean projected rotational velocities (MRPV) for 27
HAEBE stars:
![]() km s-1. The histograms of
km s-1. The histograms of ![]() distributions for HAEBE+Vega-type stars from our sample and classical Be
stars are presented in Figs. 15 and 16 respectively. Despite the fact
that both distributions are broad it is reasonably safe to suggest that these
distributions diverge considerably. Simple comparison of
distributions for HAEBE+Vega-type stars from our sample and classical Be
stars are presented in Figs. 15 and 16 respectively. Despite the fact
that both distributions are broad it is reasonably safe to suggest that these
distributions diverge considerably. Simple comparison of ![]() values
for stars of different groups leads to the following results:
the MPRV for HAEBE+Vega-type stars (164 objects) and classical Be stars are
values
for stars of different groups leads to the following results:
the MPRV for HAEBE+Vega-type stars (164 objects) and classical Be stars are
![]() 105 km s-1 and
105 km s-1 and ![]() 220 km s-1 (with the standard deviation 80 km s-1and 90 km s-1) respectively.
220 km s-1 (with the standard deviation 80 km s-1and 90 km s-1) respectively.
One can however note that comparison of the ![]() distributions is inapplicable for stars having a wide range of spectral
classes. However even for 83 Herbig Be+B Vega-type
stars the MPRV is
distributions is inapplicable for stars having a wide range of spectral
classes. However even for 83 Herbig Be+B Vega-type
stars the MPRV is ![]() 130 km s-1 or excluding a few stars which
were early classified as classical Be-105 km s-1. Various statistical tests
indicate immediately that the difference between mean values of
130 km s-1 or excluding a few stars which
were early classified as classical Be-105 km s-1. Various statistical tests
indicate immediately that the difference between mean values of ![]() for Herbig Be+B Vega-type stars and classical Be stars is
statistically significant even at 99% confidence level.
In spite of small statistics the average value of
for Herbig Be+B Vega-type stars and classical Be stars is
statistically significant even at 99% confidence level.
In spite of small statistics the average value of ![]() for young
solar-type stars is smaller than for TT stars (see Appendices 4-5).
for young
solar-type stars is smaller than for TT stars (see Appendices 4-5).
As is evident from the theory of stellar evolution, within similar spectral
classes the rotational velocities should be smaller for more evolved stars
due to the loss of AM (see for example Soderblom et al. [1993] or
Dudorov & Pudritz [1994]). However classical Be stars are
much more rapid rotators in comparison with young Herbig Be and B Vega-type
stars in spite of the former being much more evolved. On the one hand it can
be supposed that the increasing of rotational velocities in Be stars takes
place due to further contraction and the associated conservation of AM, while
a spin down for HAEBE stars is due to net AM loss (by stellar wind) as was
supposed by Finkenzeller ([1985]). But on the other hand the young
stars may lose AM by interaction with dust circumstellar shells because
classical Be stars have no dust in their environment and this is the primary
difference between them. However this leads us to conclude
possible differences in initial conditions of formation of Be and young
Herbig Be stars because if classical Be stars were surrounded by dust shells
in earlier evolutionary phases they would also have low ![]() values at
present (see also discussion in Zorec & Briot [1997]).
A detailed discussion of various mechanisms for the
redistribution of AM can be found in Brown & Verschueren ([1997]).
values at
present (see also discussion in Zorec & Briot [1997]).
A detailed discussion of various mechanisms for the
redistribution of AM can be found in Brown & Verschueren ([1997]).
An important by-product of this study is that
the average values of ![]() differ strongly for classical Be and
young HAEBE + Vega-type stars.
differ strongly for classical Be and
young HAEBE + Vega-type stars.
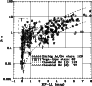 |
Figure 17:
|
Copyright The European Southern Observatory (ESO)