The theoretical scheme is described in earlier works (Hummer et al.
1993; Nahar & Pradhan 1999, 2000). We sketch the basic points below.
In the coupled channel or close coupling (CC) approximation an atom
(ion) is described in terms of an (e + ion) complex that comprises of
a "target'' ion, with N bound electrons, and a "free'' electron that may
be either bound or continuum. The total energy of the system is either
negative or positive; negative eigenvalues of the (N + 1)-electron
Hamiltonian correspond to bound states of the (e + ion) system. In the
CC approximation the wavefunction expansion, ![]() ,
for
a total spin and angular symmetry
,
for
a total spin and angular symmetry ![]() or
or ![]() ,
of the (N+1)
electron system is represented in terms of the target ion states or
levels as:
,
of the (N+1)
electron system is represented in terms of the target ion states or
levels as:
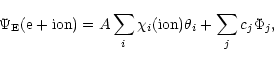 |
(1) |
where ![]() is the target ion wave function in a specific state
is the target ion wave function in a specific state
![]() or level
or level ![]() ,
and
,
and
![]() is the wave function
for the (N+1)th electron in a channel labeled as
is the wave function
for the (N+1)th electron in a channel labeled as
![]() ;
ki2 is the
incident kinetic energy. In the second sum the
;
ki2 is the
incident kinetic energy. In the second sum the ![]() 's are
correlation wavefunctions of the (N+1) electron system that (a)
compensate for the orthogonality conditions between the continuum and
the bound orbitals, and (b) represent additional short-range correlation
that is often of crucial importance in scattering and radiative CC
calculations for each
's are
correlation wavefunctions of the (N+1) electron system that (a)
compensate for the orthogonality conditions between the continuum and
the bound orbitals, and (b) represent additional short-range correlation
that is often of crucial importance in scattering and radiative CC
calculations for each ![]() .
.
The BPRM method yields the solutions of the relativistic CC equations
using the Breit-Pauli Hamiltonian for the (N+1)-electron system to
obtain the total wavefunctions
![]() (Hummer et al.1993).
The BP Hamiltonian is
(Hummer et al.1993).
The BP Hamiltonian is
| (2) |
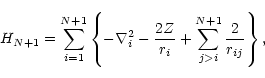 |
(3) |
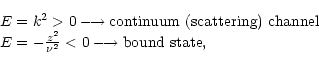 |
(4) |
The
![]() represents a CI-type wavefunction over a large number of
electronic configurations depending on the target levels included
in the eigenfunction expansion (Eq. 1). Transition matrix elements
may be calculated with these wavefunctions, and the electron dipole
(E1), electric quadrupole (E2), magnetic dipole (M1) or other operators
to obtain the corresponding transition probabilities. The present
version of the BPRM codes implements the E1 operator to enable the
calculation of dipole allowed and intercombination transition
probabilities. The oscillator strength is proportional to the
generalized line strength defined, in either length form or velocity
form, by the equations
represents a CI-type wavefunction over a large number of
electronic configurations depending on the target levels included
in the eigenfunction expansion (Eq. 1). Transition matrix elements
may be calculated with these wavefunctions, and the electron dipole
(E1), electric quadrupole (E2), magnetic dipole (M1) or other operators
to obtain the corresponding transition probabilities. The present
version of the BPRM codes implements the E1 operator to enable the
calculation of dipole allowed and intercombination transition
probabilities. The oscillator strength is proportional to the
generalized line strength defined, in either length form or velocity
form, by the equations
Using the energy difference, Eji, between the initial and final states, the oscillator strength, fij, for the transition can be obtained from S as
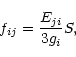 |
(7) |
and the Einstein's A-coefficient, Aji, as
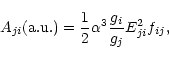 |
(8) |
where ![]() is the fine structure constant, and gi, gj are
the statistical weight factors of the initial and final states,
respectively. In cgs units,
is the fine structure constant, and gi, gj are
the statistical weight factors of the initial and final states,
respectively. In cgs units,
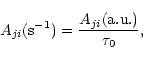 |
(9) |
where
![]() s is the atomic unit of time.
s is the atomic unit of time.
Copyright The European Southern Observatory (ESO)