6 Polrotation and intensity self-alignment

In this section I briefly review Paper II from our newly acquired viewpoint, providing proofs for its assertions and extending them. A further extension, to the case of heterogenous arrays, will follow later (Sect. 8). Here I will show how the use of an intensity calibrator suppresses polconversion and how the remaining polrotation can then be determined. The more difficult problem of eliminating poldistortion without recourse to an intensity calibrator will be taken up in Sects. 7.2 and 9.

   
6.1 Intensity self-alignment

The usual first step is to observe an unpolarized source and self-align it. Because the source has intensity only, I call this intensity self-alignment.

The brightness matrix $\vec{B}$ reduces to a positive multiple of the identity matrix I, the scale factor being the intensity. Imposing the same form on our solution, we find that

 

$$B'(\vec{l}) \mathbf{I}= \vec{X}\ B(\vec{l}) \mathbf{I}\ \vec{X}^{\dagger}.$$ (17)

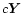A solution $\vec{B}'$ can only exist if $\vec{X}$ is a multiple $c\vec{Y}$ of a matrix $\vec{Y}$ for which

$$\begin{eqnarray*}\vec{Y}\vec{Y}^{\dagger}= \mathbf{I}, \end{eqnarray*}$$

i.e. $\vec{Y}$ is unitary. c is the scale factor discussed before and we may ignore it. What we see, then, is that the poldistortion is reduced to a polrotation, $\vec{Y}$. Our knowledge that the source is unpolarized has completely suppressed the polconversion factor $\vec{H}$ of Eq. (15). One of the central results of Paper II is that the remaining error (which we have now recognised as a polrotation) is characterised by three unknown real parameters. I have already confirmed this assertion in Sect. 5.1.

The arbitrary rotation that $\vec{Y}$ represents can be factored into the product of three mutually orthogonal rotations ([Korn & Korn 1961]). Choosing for these the base rotations of Appendix C.2 we have:

 

$${\vec{Y} = \vec{Y}_{\mathbf{q}}(\phi) \,\vec{Y}_{\mathbf{u}}(\epsilon) \,\vec{Y}_{\mathbf{v}}(\theta) }$$ (18)

$${ = \left( \begin{array}{c@{\mbox{$\!\!$ }}c} \exp i\phi &0 \\ 0... ...rr} \cos\theta & \sin\theta \\ -\sin\theta &\cos\theta \end{array} \right) . }$$

This is Eq. (27) of Paper II, revised to represent our new insight into what it actually means: The order of the factors reflects the physics of the instrument as discussed in Paper I and the variables have been renamed accordingly. The last term, which represents the first element in the signal path, corresponds to an unknown geometric rotation $\theta$ of the zero point from which the orientation of the feeds is measured; likewise, the middle term represents an unknown zero-point shift $\epsilon$ of the ellipticity scale. The leading term is the unknown phase difference $2\phi$ between the two subsets (X and Y or L and R) of receiver channels. (For circular feeds, the equation takes a different form, see Appendix C.3).

I add a new proposition. Rotating the polvector does not change its length: this means that an intensity-aligned instrument correctly measures the degree of polarization, even though the orientation of the polvector cannot be determined. This provides a simple and powerful way to detect strongly polarized sources in generally weakly polarized fields, e.g. in surveys.

   
6.2 Constraining the polrotation

To eliminate the polrotation $\vec{Y}$, Paper II proposes to observe calibrators whose polarization is known. It states that two such observations are necessary. We can now supply the proof that was missing.

Let the Stokes brightness of the first source be

$$\begin{eqnarray*}\vec{B}= [\, I +\vec{p}\,]. \end{eqnarray*}$$

We require the observed brightness $\vec{B}'$ to be the same. This limits the possible range of polrotations $\vec{Y}$ to those that conserve $\vec{p}$, i.e. those unitary transformations that have $\vec{p}$ as their rotation axis; but it leaves the rotation angle free. To constrain it as well, we do indeed need a second polarized source whose polvector is not collinear with $\vec{p}$.

   
6.3 Imposing the nominal feed characteristics

For well designed and constructed feeds, the orientations and ellipticities are quite accurately known. We may compare this prior knowledge with the polrotated Jones matrices $\vec{J}_{j \vphantom{'}}\vec{X}^{-1}$ to estimate $\vec{X}$. It is reasonable to propose that the feed errors are randomly distributed with a zero average. In this way the zero-point offsets, $\vec{Y}_{\mathbf{u}}(\epsilon)$ and $\vec{Y}_{\mathbf{v}}(\theta)$ in Eq. (18), can be eliminated. This method is discussed in Paper II and I shall return to it and to the elimination of the $\vec{Y}_{\mathbf{q}}(\phi)$ term in Sect. 8.2.

   
6.4 Calibrating polarized source fields

Elimination of poldistortion in an unpolarized field is in itself not particularly useful but, provided the instrument is stable enough, we may transfer the result to an observation of an unknown field. In this case, instrumental stability limits the accuracy of the final calibration, no matter what the theoretical potential is of the calibration methods employed.

A better option is to sidestep the problem of drifts by using supposedly unpolarized reference sources in the observed field itself. The reference can be a strong foregound source (component). At the opposite end, most fields contain many cosmic background sources whose polarization, if present at all, must be zero on the average. By analysing the source model in either case, one should be able to estimate the polconversion and correct for it.