

Up: Understanding radio polarimetry
Subsections
5 The poldistortion
5.1 Polrotation and polconversion
An arbitrary square matrix  can be subjected to a polar decomposition
(Appendix B.6)
can be subjected to a polar decomposition
(Appendix B.6)
where
- x is a complex constant;
 is a unimodular unitary matrix (i.e.
is a unimodular unitary matrix (i.e.
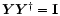 and
and
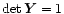 );
);
 is a unimodular positive hermitian matrix (i.e.
is a unimodular positive hermitian matrix (i.e.
 ,
,
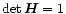 and
and
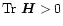 ); so is
); so is 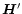 .
.
Applying the polar decomposition to Eq. (14) we get
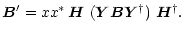 |
|
|
(15) |
The positive scaling factor is the same as in scalar selfcal and I shall further
ignore it. Apart from it,  is derived from
is derived from  through a succession of two
specific transformations.
through a succession of two
specific transformations.
The first is the unitary transformation  .
Its effect is to leave the intensity
unchanged (naturally, since
.
Its effect is to leave the intensity
unchanged (naturally, since
 )
and to rotate the polvector in
its three-dimensional space (Appendix C.1).
In quaternion notation
)
and to rotate the polvector in
its three-dimensional space (Appendix C.1).
In quaternion notation
where 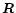 is a rotation operator. I call
is a rotation operator. I call  the polrotation
(transformation). The rotation and
the polrotation
(transformation). The rotation and  can be characterised by a vector in
polvector space, the Gibbs vector (Appendix B.1)
can be characterised by a vector in
polvector space, the Gibbs vector (Appendix B.1)
where 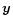 is the direction of the rotation axis and
is the direction of the rotation axis and  the rotation angle. In
Appendix C.1
I derive the relation between the Gibbs vector and
the rotation angle. In
Appendix C.1
I derive the relation between the Gibbs vector and  .
Obviously, any multiple of the Gibbs vector is an eigenvector of the
transformation:
.
Obviously, any multiple of the Gibbs vector is an eigenvector of the
transformation:
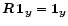 .
.
Like the polrotation, the positive hermitian transformation  is characterised by
a vector
is characterised by
a vector
that may also be called a Gibbs vector (Appendix C.4).
The transformation
exchanges brightness between the intensity and that component of the polvector that
is parallel to 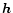 ;
any perpendicular component is an eigenvector. I call
;
any perpendicular component is an eigenvector. I call  the
polconversion. There is no mutual conversion between polvector components:
The transformation is rotation-free.
We may summarise the above by stating that the self-aligned source model
the
polconversion. There is no mutual conversion between polvector components:
The transformation is rotation-free.
We may summarise the above by stating that the self-aligned source model  is
related to the true brighness
is
related to the true brighness  by a transformation that is the product of a
polrotation, a polconversion and a positive scale factor.
The poldistortion
by a transformation that is the product of a
polrotation, a polconversion and a positive scale factor.
The poldistortion  is far more complicated than a simple scale error.
Polrotation and polconversion each contain three unknown parameters (the cartesian
components of their Gibbs vectors) which, together with the scale factor, make a
total of seven. This is the same number that Paper II arrived at through a more
elementary analysis.
is far more complicated than a simple scale error.
Polrotation and polconversion each contain three unknown parameters (the cartesian
components of their Gibbs vectors) which, together with the scale factor, make a
total of seven. This is the same number that Paper II arrived at through a more
elementary analysis.
 and
and  being unimodular
being unimodular
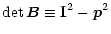 |
|
|
(16) |
is, apart from the scaling of the entire image, an invariant of the poldistortion
transformation.
5.2 Controlling the poldistortion
With self-alignment only the first half of the calibration job is done. To eliminate
the poldistortion, we must bring other information to bear on our problem. It may
take the form of either prior knowledge or additional measurements; both may be used
either to constrain the self-alignment algorithm so as to (partly) suppress the
poldistortion, or to remove the poldistortion  afterwards.
For example, if we have reason to believe that our source field is unpolarized, we
can impose this condition on our image and source model, as in Sect. 6.1
below. Alternatively, we may allow self-alignment to produce a polarized image and
determine and remove the polconversion afterwards, on the basis that in the proper
image certain sources must be unpolarized.
Apart from the image
afterwards.
For example, if we have reason to believe that our source field is unpolarized, we
can impose this condition on our image and source model, as in Sect. 6.1
below. Alternatively, we may allow self-alignment to produce a polarized image and
determine and remove the polconversion afterwards, on the basis that in the proper
image certain sources must be unpolarized.
Apart from the image  ,
self-alignment also yields estimates
,
self-alignment also yields estimates
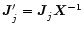 of the antenna Jones matrices. Comparing these with what we know about the
true values gives us another handle on
of the antenna Jones matrices. Comparing these with what we know about the
true values gives us another handle on  .
.


Up: Understanding radio polarimetry
Copyright The European Southern Observatory (ESO)
![]() .
Its effect is to leave the intensity
unchanged (naturally, since
.
Its effect is to leave the intensity
unchanged (naturally, since
![]() )
and to rotate the polvector in
its three-dimensional space (Appendix C.1).
In quaternion notation
)
and to rotate the polvector in
its three-dimensional space (Appendix C.1).
In quaternion notation
![]() is characterised by
a vector
is characterised by
a vector
![]() and
and ![]() being unimodular
being unimodular