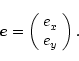Up: Understanding radio polarimetry
Subsections
2 Coherency-matrix formulation of interferometry
2.1 The scalar/matrix analogy
The algebraic properties of scalars and matrices are very similar. Every elementary
property of scalars has an immediate matrix counterpart, with one very important
exception, viz. that matrix multiplication is non-commutative.
The analogy extends further. There is, for example, a matrix counterpart of the
polar representation
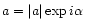 of complex numbers. An overview is
given in Table 1.
of complex numbers. An overview is
given in Table 1.
2.2 The coherency matrix
As in the previous papers of this series, I represent the electric field in
cartesian coordinates by a vector
The equivalent of the scalar visibility is the coherency tensor. In
mathematical terms, it is a complex-valued 2-dimensional tensor of rank 2
([Landau & Lifshitz 1995]). In Paper I, we represented it in the form of the coherency
vector and the Stokes vector. Here I shall use yet another representation,
the coherency matrix. It is composed of the same four elements as the
coherency vector, but arranged in the form of a
 matrix
matrix
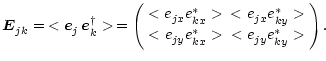 |
|
|
(1) |
All of these forms are entirely equivalent representations of one and the same
underlying tensor. Both the form (vector, matrix or other) and the coordinate system
(e.g. cartesian or circular, cf. Paper I) of the representation are a matter of
convenience. I will use geometric xy coordinates throughout.
2.3 The interferometer equation
I recall from Paper I that the elements in the signal path in one antenna transform
the electric field or voltage vector:
where
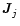 is a Jones matrix. It is then readily seen that an interferometer
with Jones matrices
is a Jones matrix. It is then readily seen that an interferometer
with Jones matrices
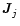 and
and
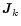 transforms the coherency matrix according to
transforms the coherency matrix according to
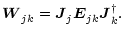 |
|
|
(2) |
Perhaps superfluously, I reiterate that this is no more than another representation
of the basic underlying transformation of the coherency tensor by an interferometer.
The advantage over the coherency-vector representation of Paper I is that both
coherencies and antenna/receiver systems are now represented by
 matrices and
we need only one type of multiplication operator. This leads to a complete formal
analogy between scalar and matrix selfcal, which will allow us to extrapolate our
knowledge of the former in trying to understand the latter.
matrices and
we need only one type of multiplication operator. This leads to a complete formal
analogy between scalar and matrix selfcal, which will allow us to extrapolate our
knowledge of the former in trying to understand the latter.
Coherency and Jones matrices having the same form, it should be clear from the
context which is which, just as in the scalar domain. In addition, note that Jones
matrices carry the single index of an antenna whereas the coherency matrices have a
double, interferometer index. This difference will remain also when we later add
another index t for sampling time.
I note in passing that in the particular case of a single dish, j=k and
Eq. (2) reduces to
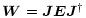 |
|
|
(3) |
which is known as a congruence transformation. We will see in
Sect. 4 that this same transformation describes a "self-aligned''
synthesis array.
2.4 Matrix and Stokes brightnesses
In its original form, the van Cittert-Zernike theorem (Paper I Appendix C;
[Thompson et al. 1986]; [Perley et al. 1994]; [Born & Wolf 1964]) establishes a spatial Fourier-transform
relation between a scalar visibility function
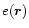 of baseline
of baseline 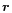 and a
scalar brightness function
and a
scalar brightness function
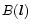 of sky position
of sky position 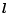 .
.
In an observation, we measure the visibility at discrete times t; our observables
are the samples
In self-calibration theory, the sampling times are assumed to coincide for all
interferometers. Also discretising the brightness, we approximate the Fourier
integral by a sum
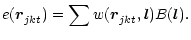 |
|
|
(4) |
The theorem can be readily generalised to show that each element of the coherency
matrix is the Fourier transform of the corresponding element of a brightness
matrix. In the same approximation
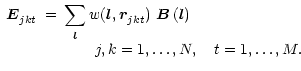 |
|
|
(5) |
The four elements of the brightness matrix correspond to those of the coherency
matrix. A more enlightening representation is provided by the Stokes
brightness (I,Q,U,V). It is another function of 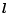 ,
defined by the
transformation
,
defined by the
transformation
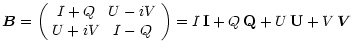 |
|
|
(6) |
where
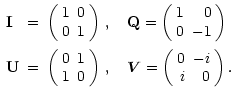 |
|
|
(7) |
The matrix constants
I,
Q,
U and 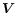 are known in physics as the
Pauli (spin) matrices.
are known in physics as the
Pauli (spin) matrices.
The Stokes parameter I is the total brightness or intensity. For (Q,U,V) a proper name is the "polarized-brightness vector''; more conveniently, I shall call
it the polvector. The dichotomy between I and the other Stokes parameters
can be understood as a consequence of the Pauli matrix
I being the identity
matrix. The domain of the polvector is closely related to that of the Poincaré
sphere ([Born & Wolf 1964]; [Cornbleet 1976];
[Simmons & Guttman 1970]).
It is convenient to introduce a shorthand for Eq. (6):
![$\displaystyle \vec{B}(\vec{l}) = [\, I(\vec{l}) + \vec{p}(\vec{l}) \,]$](/articles/aas/full/2000/09/h1201/img45.gif) |
|
|
(8) |
where
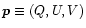 is the polvector.
is the polvector.
2.5 Quaternions
The transformation Eq. (6) or Eq. (8) does not depend on  being a
brightness matrix. It can be applied to an arbitrary
being a
brightness matrix. It can be applied to an arbitrary
 matrix
matrix  :
:
![$\displaystyle \vec{A}= [\, a + \vec{a}\,].$](/articles/aas/full/2000/09/h1201/img48.gif) |
|
|
(9) |
The entity in square brackets is known as a quaternion. Quaternions were
invented and named by Hamilton in the middle of the nineteenth century in a
mathematical quest for generalisations of the concept of complex numbers. Physicists
of the time ignored them in favour of the vector algebra that was developed at the
same time ([Hestenes 1986]). In the analysis to be presented here they prove to be
extremely useful, because they can be added and multiplied in exactly the same way
that matrices can: in mathematical terms the "quaternion group is isomorphous with
the group of
 matrices''.
([Korn & Korn 1961]).
matrices''.
([Korn & Korn 1961]).
In the same way that the Stokes vector is preferable because of its physical
content, the quaternion form of equations such as the interferometer equation
Eq. (2) can be analysed in a more meaningful way than the corresponding
matrix equations. The analysis is an essential part of this paper, but I have chosen
to present it in an appendix. In the main text, I concentrate on the results and
their physical interpretation.
The notation for quaternions is not standardised. The form Eq. (9) is an ad-hoc
choice of my own.


Up: Understanding radio polarimetry
Copyright The European Southern Observatory (ESO)
![]() of complex numbers. An overview is
given in Table 1.
of complex numbers. An overview is
given in Table 1.