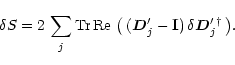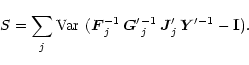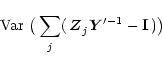Up: Understanding radio polarimetry
Subsections
D. Matrix solution techniques
The methods discussed in this paper require nonlinear minimisation of the variance
of a function of several matrices wrt one of them. One way to handle it is by
writing out all equations and their derivatives in terms of the real and imaginary
parts of all matrix elements and then applying standard nonlinear solution methods
([Press et al. 1989]). This is the approach used in AIPS++ (1998); it is cumbersome and
the resultant code is complex and difficult to verify (T. Cornwell, private
communication).
In the methods to be described below, entire matrices are the atomic variables.
Thus, full advantage is taken of the conceptual efficiency of matrix algebra, which
in turn reflects in simple solution algorithms that are very easily coded. The
algorithms explicitly exploit the structure of the equations; for this reason they
may well be more efficient than the general-purpose approach. They also lend
themselves to quick experiments in an environment such as AIPS++ (1998) in which
matrix operations can be coded directly.
D.1. Differentiation
The problem is that of finding the matrix 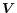 that minimises the variance of some
matrix function
that minimises the variance of some
matrix function  of
of 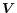 .
Attacking this problem in the conventional way
requires the definition of the derivative of
.
Attacking this problem in the conventional way
requires the definition of the derivative of
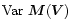 with respect to
with respect to 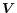 .
An
equivalent approach that requires no new definitions is to consider the
differentials themselves rather than their quotient.
For a variation
.
An
equivalent approach that requires no new definitions is to consider the
differentials themselves rather than their quotient.
For a variation
 ,
the corresponding variation in
,
the corresponding variation in
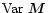 is
(cf. Eq. 41)
is
(cf. Eq. 41)
In the applications of interest,
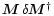 is a sum of (products of) several
other matrices, one of which is
is a sum of (products of) several
other matrices, one of which is
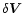 .
In each of these products, we may
cyclically permute the factors to move
.
In each of these products, we may
cyclically permute the factors to move
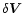 to the trailing position (cf.
Appendix C.5).
Thus we convert each product term in Eq. (43) to the form
to the trailing position (cf.
Appendix C.5).
Thus we convert each product term in Eq. (43) to the form
 |
|
|
(44) |
If 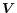 is constrained, e.g. to being diagonal or unitary, corresponding constraints
are to be imposed upon
is constrained, e.g. to being diagonal or unitary, corresponding constraints
are to be imposed upon
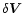 .
.
If, for any permitted variation
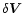 ,
the variation
,
the variation
 is also
allowed, Eq. (44) can be simplified by omitting the
is also
allowed, Eq. (44) can be simplified by omitting the
 operator. If,
moreover,
operator. If,
moreover,
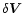 is completely free, Eq. (44) implies that
is completely free, Eq. (44) implies that  itself is
itself is
 .
.
D.2. Self-alignment decomposition
I show a simple least-squares self-aligment algorithm as an example. Given a set of
observed coherencies
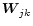 and a source model
and a source model
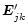 ,
we seek to fit values
,
we seek to fit values
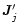 that minimise the noise power at the interferometer inputs:
that minimise the noise power at the interferometer inputs:
For a change
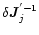 we have, from Eq. (43)
we have, from Eq. (43)
Since
 is arbitrary, it follows that
is arbitrary, it follows that
Given a set of estimates
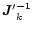 ,
this equation provides the basis for an iterative
algorithm by producing a new estimate for
,
this equation provides the basis for an iterative
algorithm by producing a new estimate for
 .
.
Note the similarity of the first three factors on the lefthand side to
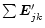 .
In the same way as dimension comparisons in physics, this similarity
provides a partial check on the correctness of an equation.
.
In the same way as dimension comparisons in physics, this similarity
provides a partial check on the correctness of an equation.
This method is easily generalised to a more proper 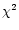 form for the case where
the four polarisation channels in each interferometer carry the same noise level.
This is probably an adequate assumption in most practical cases.
form for the case where
the four polarisation channels in each interferometer carry the same noise level.
This is probably an adequate assumption in most practical cases.
D.3. Feed-error minimisation
Section 8.2 poses the problem of minimising
 |
|
|
(45) |
where
 are unknown diagonal gain matrices and
are unknown diagonal gain matrices and  is the unknown unitary
polrotation matrix (which is not necessarily unimodular). Taking differentials
is the unknown unitary
polrotation matrix (which is not necessarily unimodular). Taking differentials
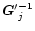 is found given the current value of
is found given the current value of  in the way indicated above. The
constraint on
in the way indicated above. The
constraint on
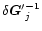 is that it be diagonal. The result is
is that it be diagonal. The result is
To solve for  given the current values of the
given the current values of the
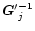 ,
we begin by applying
unitary transformations
,
we begin by applying
unitary transformations
 to the summands in Eq. (45) to obtain (cf.
Appendix A.5)
to the summands in Eq. (45) to obtain (cf.
Appendix A.5)
We may now minimise S by invoking the minimum-variance theorem of
Appendix C.5,
in combination with the fact that
and
are minimal for the same value of  .
.


Up: Understanding radio polarimetry
Copyright The European Southern Observatory (ESO)
![]() ,
the variation
,
the variation
![]() is also
allowed, Eq. (44) can be simplified by omitting the
is also
allowed, Eq. (44) can be simplified by omitting the
![]() operator. If,
moreover,
operator. If,
moreover,
![]() is completely free, Eq. (44) implies that
is completely free, Eq. (44) implies that ![]() itself is
itself is
![]() .
.
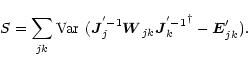
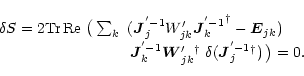

![]() .
In the same way as dimension comparisons in physics, this similarity
provides a partial check on the correctness of an equation.
.
In the same way as dimension comparisons in physics, this similarity
provides a partial check on the correctness of an equation.
![]() form for the case where
the four polarisation channels in each interferometer carry the same noise level.
This is probably an adequate assumption in most practical cases.
form for the case where
the four polarisation channels in each interferometer carry the same noise level.
This is probably an adequate assumption in most practical cases.