

Up: Understanding radio polarimetry
Subsections
C. Congruence transformations
The congruence transformation is defined in
Eqs. (3) and (14). Substituting the polar decomposition for  we get
Eq. (15):
we get
Eq. (15):
Since  and
and  are unimodular,
are unimodular,
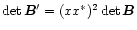 or, apart from
the scale factor
or, apart from
the scale factor
(In the main text of this paper, b and 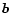 are written as I and
are written as I and  ,
respectively, to emphasize the physical interpretation of
,
respectively, to emphasize the physical interpretation of  as a brightness.)
as a brightness.)
The effect of the component unitary and positive hermitian transformations can now
be analysed by replacing  ,
,
 and
and  with their equivalent quaternions and
carrying out the multiplications:
with their equivalent quaternions and
carrying out the multiplications:
C.1. Unitary transformations
Consider the most general unitary transformation
where
 and
and
 are the components of
are the components of 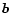 that are parallel and
perpendicular to
that are parallel and
perpendicular to
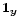 .
.
The unitary quaternions are collinear with
![$[\, b + \vec{b}_{\scriptscriptstyle\parallel \vphantom{'}}\,]$](/articles/aas/full/2000/09/h1201/img210.gif) so
so
For
 we must carry out the multiplications, and obtain
we must carry out the multiplications, and obtain
That is,
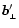 is a copy of
is a copy of
 rotated over an angle
rotated over an angle  .
The two results combined show that a unitary transformation
.
The two results combined show that a unitary transformation  leaves the scalar
part of its input invariant and rotates its vector part around the axis
leaves the scalar
part of its input invariant and rotates its vector part around the axis
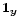 over an angle
over an angle  ;
this is the polrotation effect of
Sect. 5.1. The scalar and vector parts are transformed
independently.
;
this is the polrotation effect of
Sect. 5.1. The scalar and vector parts are transformed
independently.
The vector
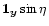 that characterises the rotation is known as the
Gibbs vector ([Korn & Korn 1961]). Vectors collinear with it are invariant; they are
eigenvectors of the rotation.
that characterises the rotation is known as the
Gibbs vector ([Korn & Korn 1961]). Vectors collinear with it are invariant; they are
eigenvectors of the rotation.
From the theory of linear transformations I take the result that the mathematical
expression for a rotation is
where the
 transformation matrix
transformation matrix 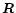 is real, orthogonal
and unitary.
Its unitarity guarantees the invariance of scalar products and in particular of real
vector lengths.
is real, orthogonal
and unitary.
Its unitarity guarantees the invariance of scalar products and in particular of real
vector lengths.
The Euclidian rotations of the vector part 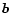 form a subset of the general
pseudo-Euclidian rotations represented by the Lorentz transformation
([Feynman et al. 1975]), just as the unitary transformations form a subset of the general
congruence transformations.
form a subset of the general
pseudo-Euclidian rotations represented by the Lorentz transformation
([Feynman et al. 1975]), just as the unitary transformations form a subset of the general
congruence transformations.
C.2. The fundamental unitary matrices
Any rotation in a three-dimensional Euclidian space can be represented as a
succession of three rotations around mutually perpendicular axes ([Korn & Korn 1961]).
Choosing for these axes the three base vectors of Eq. (28) we find the three
respective basic unimodular unitary matrices
-
The phase-difference transformation
![$\displaystyle \vec{Y}_{\mathbf{q}}(\phi) = \left( \begin{array}{cc} \exp i\phi & 0
\\ 0 &\exp -i\phi \end{array} \right)
= \exp i\,[\vec{1}_{\mathbf{q}}]\phi .$](/articles/aas/full/2000/09/h1201/img217.gif) |
|
|
(36) |
-
The ellipticity transformation
![$\displaystyle \vec{Y}_{\mathbf{u}}(\epsilon) = \left( \begin{array}{rr} \cos\ep...
...n & \cos\epsilon \end{array} \right)
= \exp i\,[\vec{1}_{\mathbf{u}}]\epsilon .$](/articles/aas/full/2000/09/h1201/img218.gif) |
|
|
(37) |
-
The (feed or xy frame) rotation transformation
![$\displaystyle \vec{Y}_{\mathbf{v}}(\theta) = \left( \begin{array}{rr} \cos\thet...
...\theta &\cos\theta \end{array} \right)
= \exp i\,[\vec{1}_{\mathbf{v}}]\theta .$](/articles/aas/full/2000/09/h1201/img219.gif) |
|
|
(38) |
C.3. The polrotation in circular coordinates
It is of some interest to consider the form that Eq. (18) takes in circular
coordinates. The feed and receiver terms
 and
and
 operate on the signal
vector formed by the l and r voltages in the feed-receiver system and need not
change. The geometric rotation term
operate on the signal
vector formed by the l and r voltages in the feed-receiver system and need not
change. The geometric rotation term
 must be transformed to the
circular lr coordinate frame (Paper I) in which the radiation is measured. From
Paper I we take the result that this transformation transforms Stokes V into Q,
hence
must be transformed to the
circular lr coordinate frame (Paper I) in which the radiation is measured. From
Paper I we take the result that this transformation transforms Stokes V into Q,
hence
 into
into
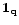 .
Thus
.
Thus
 assumes the form
assumes the form
 ,
and the equivalent of Eq. (18) becomes
,
and the equivalent of Eq. (18) becomes
 |
|
|
(39) |
This is another generic way of factoring an arbitrary rotation ([Korn & Korn 1961]).
When the feed-error term
 is reduced to unity, the remaining two
is reduced to unity, the remaining two
 terms
fuse into one. The usual practice of merging them regardless of the feed errors
amounts to inverting the order of the factors in Eq. (39); this is justifiable
only in the quasi-scalar approximation (cf. Sect. 7).
terms
fuse into one. The usual practice of merging them regardless of the feed errors
amounts to inverting the order of the factors in Eq. (39); this is justifiable
only in the quasi-scalar approximation (cf. Sect. 7).
C.4. Positive hermitian transformations
The treatment of the unimodular positive hermitian transformation is analogous to
that of the unitary one. Starting from Eq. (33) for  one finds
one finds
 |
|
|
(40) |
The effect is in a sense complementary to that of the unitary transformation, but
there is no analogous geometric interpretation. The scalar and vector parts are not
transformed independently but get mixed: this is the polconversion effect of
Sect. 5.1.
There is no interaction between vector components in different directions: The
transformation is said to be rotation-free.
C.5. Minimal-variance theorem
Of all complex numbers
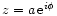 ,
z=a has the smallest distance squared
|(z-1)|2 to unity. I shall now prove an analogous property for
,
z=a has the smallest distance squared
|(z-1)|2 to unity. I shall now prove an analogous property for
 matrices:
matrices:
Theorem: Let  be a given positive hermitian and
be a given positive hermitian and  an arbitrary unitary
matrix. Of all products
an arbitrary unitary
matrix. Of all products
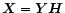 ,
,
 minimises the quantity
minimises the quantity
Using the definition of
 ,
the commutation and transposition invariance of
,
the commutation and transposition invariance of
 and the hermiticity of
and the hermiticity of  ,
convert the equation to
,
convert the equation to
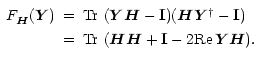 |
|
|
(41) |
To find the minimum, consider the term
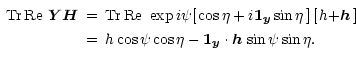 |
|
|
(42) |
Differentiation with respect to  and
and 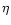 gives the equations
gives the equations
whose obvious solutions are
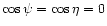 and
and
 .
.
Since  is positive hermitian,
is positive hermitian,
so a. there are no other solutions and b. the former one, which is
equivalent to
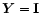 ,
maximises Eq. (42) and hence minises
,
maximises Eq. (42) and hence minises
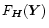 .
Moreover this is true for all directions
.
Moreover this is true for all directions
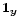 .
.


Up: Understanding radio polarimetry
Copyright The European Southern Observatory (ESO)
![]() and
and ![]() are unimodular,
are unimodular,
![]() or, apart from
the scale factor
or, apart from
the scale factor
![]() ,
,
![]() and
and ![]() with their equivalent quaternions and
carrying out the multiplications:
with their equivalent quaternions and
carrying out the multiplications:
![\begin{eqnarray*}\lefteqn{ [\, b'+\vec{b}'_{\scriptscriptstyle\parallel \vphanto...
...\rm e}^{-i\psi} [\, \cos\eta {-} i\vec{1}_{\vec{y}}\sin\eta \,]
\end{eqnarray*}](/articles/aas/full/2000/09/h1201/img206.gif)
![]() so
so
![]() that characterises the rotation is known as the
Gibbs vector ([Korn & Korn 1961]). Vectors collinear with it are invariant; they are
eigenvectors of the rotation.
that characterises the rotation is known as the
Gibbs vector ([Korn & Korn 1961]). Vectors collinear with it are invariant; they are
eigenvectors of the rotation.
![]() form a subset of the general
pseudo-Euclidian rotations represented by the Lorentz transformation
([Feynman et al. 1975]), just as the unitary transformations form a subset of the general
congruence transformations.
form a subset of the general
pseudo-Euclidian rotations represented by the Lorentz transformation
([Feynman et al. 1975]), just as the unitary transformations form a subset of the general
congruence transformations.
![]() is reduced to unity, the remaining two
is reduced to unity, the remaining two
![]() terms
fuse into one. The usual practice of merging them regardless of the feed errors
amounts to inverting the order of the factors in Eq. (39); this is justifiable
only in the quasi-scalar approximation (cf. Sect. 7).
terms
fuse into one. The usual practice of merging them regardless of the feed errors
amounts to inverting the order of the factors in Eq. (39); this is justifiable
only in the quasi-scalar approximation (cf. Sect. 7).
![]() be a given positive hermitian and
be a given positive hermitian and ![]() an arbitrary unitary
matrix. Of all products
an arbitrary unitary
matrix. Of all products
![]() ,
,
![]() minimises the quantity
minimises the quantity
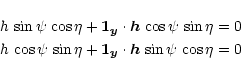
![]() is positive hermitian,
is positive hermitian,