

Up: Understanding radio polarimetry
Subsections
B. Special matrices
B.1. Unitary matrices
A
 matrix
matrix  is unitary if
is unitary if
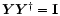 .
To derive its quaternion
form I cast the most general quaternion
.
To derive its quaternion
form I cast the most general quaternion
![$[\, a+\vec{a}\,]$](/articles/aas/full/2000/09/h1201/img154.gif) in the form
in the form
![$\displaystyle \vec{Y}= {\rm e}^{i\xi}\, [\, y + {\vec{x}}+ i\,\vec{y}\,]
\,, \quad y, {\vec{x}}, \vec{y}\mbox{ real} .$](/articles/aas/full/2000/09/h1201/img172.gif) |
|
|
(31) |
I now expand
 in quaternion form and require that it equal
I:
in quaternion form and require that it equal
I:
Since
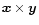 is perpendicular to
is perpendicular to  ,
the vector part in the product can
vanish only if
,
the vector part in the product can
vanish only if
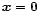 .
It follows that
.
It follows that
Now, if  is to be unimodular,
is to be unimodular,  must be 0. Hence we may rewrite Eq. (31)
as
must be 0. Hence we may rewrite Eq. (31)
as
 = =![$\displaystyle [\, \cos\eta + i \vec{1}_{\vec{y}} \sin\eta \,]$](/articles/aas/full/2000/09/h1201/img180.gif) |
(32) |
 is completely defined by the three real components of its Gibbs vector
([Korn & Korn 1961])
is completely defined by the three real components of its Gibbs vector
([Korn & Korn 1961])
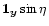 .
Since
.
Since
 ,
it can be shown from the Taylor-series expansions of
the cosine and sine functions that
,
it can be shown from the Taylor-series expansions of
the cosine and sine functions that
and hence
For small 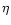 ,
we may replace the exponential by its first-order approximation.
The value of
,
we may replace the exponential by its first-order approximation.
The value of 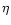 then provides a direct measure for the deviation of
then provides a direct measure for the deviation of  from
I.
from
I.
B.2. Complex linear polarized brightness
In the quasi-linear treatment of polarization, the linearly polarized visibility and
brightness frequently appear in the form of the complex variable Q+iU, cf.
(Eq. 19). This form is directly related to the quaternion exponential
above.
In particular, for a unit vector in the
q,u plane of quaternion-vector space
B.3. Unitary Jones matrices and perfect feeds
In Sect. 8 unitary Jones matrices were postulated. Since
 ,
a
feed with such a matrix transfers all incident radiation to its output: it must be
loss-free and matched at its in- and outputs. Matching implies that either receptor
must absorb all the radiation that the other one does not: the receptors must be of
opposite polarizations ([Born & Wolf 1964]; [Cornbleet 1976]; [Thompson et al. 1986]).
,
a
feed with such a matrix transfers all incident radiation to its output: it must be
loss-free and matched at its in- and outputs. Matching implies that either receptor
must absorb all the radiation that the other one does not: the receptors must be of
opposite polarizations ([Born & Wolf 1964]; [Cornbleet 1976]; [Thompson et al. 1986]).
This is the way feeds for radio telescopes are normally designed. Note, however,
that e.g. a stationary pair of crossed dipole receptors is not matched to radiation
from an arbitrary direction. Designs for arrays of phased dipoles will have to take
the problems ensuring into account.
B.4. Positive hermitian matrices
 is hermitian or self-adjoint if
is hermitian or self-adjoint if
 ;
since the Pauli
matrices are hermitian, the quaternion form
;
since the Pauli
matrices are hermitian, the quaternion form
![$\vec{H}= [\, h + \vec{h}\,]$](/articles/aas/full/2000/09/h1201/img187.gif) of a hermitian
of a hermitian
 matrix is real, cf. Eq. (23). A
matrix is real, cf. Eq. (23). A
 matrix is positive if its
eigenvalues are both positive. An equivalent condition is that both its trace and
its determinant are positive.
matrix is positive if its
eigenvalues are both positive. An equivalent condition is that both its trace and
its determinant are positive.
For the matrix to be positive hermitian and unimodular
We may then write it as
![$\displaystyle \vec{H}= \cosh\gamma + [\, \vec{1}_{\vec{h}} \,] \sinh\gamma
\equiv \exp \,[\, \vec{1}_{\vec{h}} \,] \,\gamma .$](/articles/aas/full/2000/09/h1201/img189.gif) |
|
|
(33) |
It is completely defined by the three real components of
 which I will also call a Gibbs vector.
It is readily shown from Eq. (33) that
which I will also call a Gibbs vector.
It is readily shown from Eq. (33) that
![$\displaystyle \vec{H}^2 = \exp \,[\, \vec{1}_{\vec{h}} \,] \,2\gamma .$](/articles/aas/full/2000/09/h1201/img191.gif) |
|
|
(34) |
B.5. Matrix square root
We will need the positive hermitian square root  of the product
of the product
 for an
arbitrary
for an
arbitrary
 matrix
matrix  .
Let
.
Let
Then
is readily shown to be positive hermitian. We now seek to find a positive hermitian
matrix  such that
such that
 ,
that is
,
that is
 |
|
|
(35) |
Conceptually the simplest way to find the root is through
Eqs. (33) and (34). Computationally it is more efficient to solve
the quadratic equation that Eq. (35) represents. Out of four possible
solutions, the positive definite one is
B.6. Polar decomposition
An arbitrary matrix  can be represented ([Lancaster & Tismenetsky 1985]) as the product of a
unitary and a positive hermitian matrix:
can be represented ([Lancaster & Tismenetsky 1985]) as the product of a
unitary and a positive hermitian matrix:
This is the matrix/quaternion analogue of the polar form of a complex scalar.
Defining
we may rewrite the decomposition as
where  and
and  are now unimodular.
To find
are now unimodular.
To find  we form the product
we form the product
and find  by taking the positive hermitian square root.
by taking the positive hermitian square root.


Up: Understanding radio polarimetry
Copyright The European Southern Observatory (ESO)
![\begin{eqnarray*}\vec{Y}\,\vec{Y}^{\dagger}&=& [\, y + {\vec{x}}+ i\,\vec{y}\,] ...
...^2
+ 2 (y{\vec{x}}+ \,{\vec{x}}\times\vec{y}) \,] = [\,1\,] .
\end{eqnarray*}](/articles/aas/full/2000/09/h1201/img174.gif)
![\begin{eqnarray*}[\, \vec{1}_{\mathbf{q}}\cos\phi +\vec{1}_{\mathbf{u}}\sin\phi ...
...\mathbf{q}}\,] \,\exp -i\,[\, \vec{1}_{\mathbf{v}} \,] \,\phi .
\end{eqnarray*}](/articles/aas/full/2000/09/h1201/img186.gif)
![\begin{eqnarray*}\vec{H}&=& \sqrt{(\, a + \sqrt{ a^2 - \vec{a}^2 } \;) /2 }
\\ &...
...vec{a}} \,] \,\sqrt{ (\, a - \sqrt{ a^2 - \vec{a}^2 }\;) /2 } .
\end{eqnarray*}](/articles/aas/full/2000/09/h1201/img198.gif)