

Up: Understanding radio polarimetry
Subsections
A. Quaternion algebra
Quaternions are not part of the standard mathematical toolkit of physicists and
engineers. They do find applications in the practical calculation of rotations, e.g.
in computer animation, but the relevant texts concentrate on that particular
application (e.g. [Kuipers 1998]; see also many entries on the World-Wide Web). In
scientific textbooks (e.g. [Cornbleet 1976]; [Korn & Korn 1961]) one may find brief
references to them but hardly anything more. Hestenes (1986) mentions them as a
variant of the concepts of bivectors and spinors that have a more
central place in his text, and most of the concepts that we need are to be found
there in one form or another; however, his work is not very accessible as a quick
reference. For lack of better, I give here a brief summary of quaternion theory in
the form in which I use it.
In the algebraic view, the vector part of a quaternion is a generalisation of the
imaginary part of a complex number; correspondingly, the scalar and vector
components are real and the square of a unit vector equals -1. Hestenes' version
of quaternions emphasises the geometrical viewpoint that also underlies my work; it
is then more appropriate for a unit vector squared to equal +1, which is achieved by
inserting factors
 in the Pauli-matrix definitions. Another departure
from the algebraic approach is that we explicitly allow the coefficients to be
complex. The reader consulting literature on quaternions should be aware of these
possible differences.
in the Pauli-matrix definitions. Another departure
from the algebraic approach is that we explicitly allow the coefficients to be
complex. The reader consulting literature on quaternions should be aware of these
possible differences.
Another connection that looks interesting is that with the theory of special
relativity, in which four-vectors appear with three spatial and one temporal
component. The discussion of the Lorentz transformation by Feynman et al. (1975) shows a
close formal analogy with my poldistortions (which was recently also noted by
[Britton 2000]), but I have found no useful inspiration in it.
I derive here the algebraic rules that quaternions must follow to make them behave
in the same way as the equivalent matrices.
Once we have these rules in place we may proclaim, in mathematical language, that
the multiplicative quaternion group and the multiplicative group of
 matrices are isomorphous ([Korn & Korn 1961]). In simpler terms, we may consider "
matrices are isomorphous ([Korn & Korn 1961]). In simpler terms, we may consider "
 matrix'' and "quaternion'' as names for the same object in two different languages, or
even as synonyms. Such phrases as "the scalar and vector parts of a matrix'' will
then make sense.
matrix'' and "quaternion'' as names for the same object in two different languages, or
even as synonyms. Such phrases as "the scalar and vector parts of a matrix'' will
then make sense.
In Table 3 I present a dictionary for translating from matrix to
quaternion language.
A.1. Addition
I start from the matrix/quaternion equivalence of Sect. 2.5:
The use of the "+'' sign is justified by the expansion that the right-hand side
actually represents:
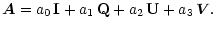 |
|
|
(22) |
The addition rules for quaternions are the obvious ones as can be shown in the same
way.
A.2. Transposition and conjugation
The definition of the vector part of a quaternion does not specify whether it is a
row or column vector and the same is true for the dot and cross products that we
will need later.
Since the Pauli matrices are hermitian, it follows that
![$\displaystyle \vec{A}^{\dagger}= [\, a^* + \vec{a}^* \,] .$](/articles/aas/full/2000/09/h1201/img147.gif) |
|
|
(23) |
A.3. Multiplication
The following identities follow directly from the definitions Eq. (7) of the
Pauli matrices:
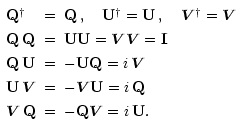 |
|
|
(24) |
Now consider the product
Writing out the expansions Eq. (22) for  and
and  and multiplying term
by term using Eq. (24), one finds the multiplication rule
and multiplying term
by term using Eq. (24), one finds the multiplication rule
![$\displaystyle [\, a+\vec{a}\,]\,[\, b+\vec{b}\,]
= [\, (ab + \vec{a}\!\cdot\!\vec{b}) + (a\vec{b}+ b\vec{a}+ i\vec{a}\times\vec{b}) \,] .$](/articles/aas/full/2000/09/h1201/img150.gif) |
|
|
(25) |
An important corrolary is that
![$[\, \vec{1}_{{\vec{x}}} \,]^2 = [\, 1 \,]$](/articles/aas/full/2000/09/h1201/img151.gif) for any unit
vector
for any unit
vector
 .
Like the multiplication of the equivalent matrices, quaternion multiplication is
generally non-commutative. An exception occurs when
.
Like the multiplication of the equivalent matrices, quaternion multiplication is
generally non-commutative. An exception occurs when 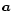 and
and 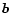 are collinear so
that
are collinear so
that
 .
In that case I also call the matrices/quaternions
.
In that case I also call the matrices/quaternions
![$[\, a+\vec{a}\,]$](/articles/aas/full/2000/09/h1201/img154.gif) and
and
![$[\, b+\vec{b}\,]$](/articles/aas/full/2000/09/h1201/img155.gif) collinear.
collinear.
Also note that the product of two real quaternions is not real unless they commute.
The corresponding matrix property is that the product of two hermitian matrices is
generally non-hermitian.
A.4. Scalars as quaternions
The scalar quaternion ![$[\,a\,]$](/articles/aas/full/2000/09/h1201/img156.gif) represents the
represents the
 matrix
aI, and
since
matrix
aI, and
since
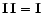 ,
both the addition and the multiplication rule for scalar
quaternions are the same as those for scalars. We may consider scalars as a subset
of the quaternions:
,
both the addition and the multiplication rule for scalar
quaternions are the same as those for scalars. We may consider scalars as a subset
of the quaternions:
A.5. Determinant, trace and variance
Every familiar property of a
 matrix has a quaternion counterpart. Thus a
quaternion has a determinant
matrix has a quaternion counterpart. Thus a
quaternion has a determinant
![$\displaystyle \det [\, a+\vec{a}\,] = a^2 - \vec{a}^2$](/articles/aas/full/2000/09/h1201/img159.gif) |
|
|
(26) |
and
 .
A unimodular matrix/quaternion is one whose
determinant equals 1.
.
A unimodular matrix/quaternion is one whose
determinant equals 1.
The trace is
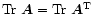 ,
,
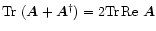 ,
and
,
and
 .
The coefficients of the Pauli matrices in Eq. (7) are given by expressions
such as
.
The coefficients of the Pauli matrices in Eq. (7) are given by expressions
such as
The trace is invariant under a unitary transformation:
I define the variance of a matrix as the sum of the moduli squared of its
elements. It is the square of the "Frobenius norm'' ([Lancaster & Tismenetsky 1985]) and given by
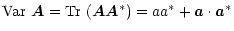 |
|
|
(27) |
 may be used as a measure of "how different''
may be used as a measure of "how different''  and
and  are. It is
readily shown that, like the trace, the variance is also invariant under unitary
transformations.
are. It is
readily shown that, like the trace, the variance is also invariant under unitary
transformations.
A.6. Coordinate systems
The vector parts of quaternions form a three-dimensional quaternion-vector
space. It is convenient to choose the coordinates in this space in accordance with
our definition of the Stokes quaternion.
When we express the electric field vectors in geometric xy coordinates, and use
the conventional definition of the Stokes vector (cf. Paper I), the definition
Eq. (6) follows. The corresponding base vectors are the quaternion vectors
corresponding to the Pauli matrices
Q,
U and 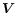 :
:
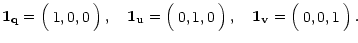 |
|
|
(28) |
Analogously to Eq. (24) we have
![$\displaystyle [\vec{1}_{\mathbf{q}}] \,[\vec{1}_{\mathbf{u}}]
= -[\vec{1}_{\mathbf{u}}] \,[\vec{1}_{\mathbf{q}}] = i \,[\vec{1}_{\mathbf{v}}]
\qquad\mbox{etc.}$](/articles/aas/full/2000/09/h1201/img170.gif) |
|
|
(29) |
If, instead, we use circular rl coordinates to describe the electric field, this
results in a cyclic permutation of the coordinate axes (Paper I) and instead of
Eq. (22) we have
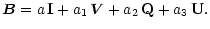 |
|
|
(30) |
This form is convenient for analysing systems with nominally circular feeds.


Up: Understanding radio polarimetry
Copyright The European Southern Observatory (ESO)
![]() in the Pauli-matrix definitions. Another departure
from the algebraic approach is that we explicitly allow the coefficients to be
complex. The reader consulting literature on quaternions should be aware of these
possible differences.
in the Pauli-matrix definitions. Another departure
from the algebraic approach is that we explicitly allow the coefficients to be
complex. The reader consulting literature on quaternions should be aware of these
possible differences.
![]() matrices are isomorphous ([Korn & Korn 1961]). In simpler terms, we may consider "
matrices are isomorphous ([Korn & Korn 1961]). In simpler terms, we may consider "
![]() matrix'' and "quaternion'' as names for the same object in two different languages, or
even as synonyms. Such phrases as "the scalar and vector parts of a matrix'' will
then make sense.
matrix'' and "quaternion'' as names for the same object in two different languages, or
even as synonyms. Such phrases as "the scalar and vector parts of a matrix'' will
then make sense.