2 Method of calculation

Each atom is a many-body system which may be described by an independent-particle-model. In this model, each electron moves independently in an effective potential determined by the nucleus and the other electrons. The potential for an electron in a neutral or ionized atom is assumed to have the form

$$V({r}) = - \left( 2/{r} \right) \{(Z-\eta) [H ({\rm e}^{{r}/{d}} -1)+1 ]^{-1}+\eta \}$$ (1)

where Z is the atomic number, and 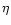$\eta$ is the ionicity: $\eta =1$, 2, 3 for As I, As II, As III, respectively. The quantity r is the electron-nucleus distance, and d, H are adjustable parameters. The potential of equation (1) is inserted into the radial Schrödinger equation, which is then solved to obtain the energy eigenvalues and wave functions. The parameters d, H are adjusted so as to obtain agreement between the energy eigenvalues and the experimental single-particle energy levels. This procedure and all necessary formulas may be found in a previous article ([Ganas 1995]). The following values of the potential parameters were obtained: d = 1.4196, H = 8.1745 for As I; d = 4.7814, H = 39.726 for As II; d = 0.6094, H = 3.0641 for As III.

Representative energy levels are given in Table 1 for As III. The computed levels and the experimental levels are in good agreement, the discrepancy being less than 2% in every case (except one).

 

Table 2: Oscillator strengths, f, for the resonance transition 4p³(⁴S 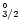$^{\circ }_{3/2}$) $\rightarrow$4p²(³P)5s(⁴P_J) in As I, from the present calculations, other calculations, and experiment

J	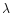$\lambda$(Å)	f (this	f	f (other
		calculation)	(experiment)	calculations)
1/2	1972.6	0.0532	$0.059 \pm 0.008^a$	0.0584d
			0.074b, 0.0734c	0.06e, 0.03f
3/2	1937.6	0.1064	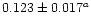$0.123 \pm 0.017^a$	0.113d
			0.14b, 0.139c	0.11e, 0.06f
5/2	1890.4	0.1596	0.21b, 0.214c	0.161d, 0.16e

^a

Bengtsson et al. (1992): uses time-resolved laser spectroscopy.

^b

Andersen et al. (1974): uses the beam-foil technique.

^c

Lotrian et al. (1980): uses emission spectroscopy.

^d

Verner et al. (1994): gives a critical review of f-values from previous compilations.

^e

Holmgren (1975): uses optimized Hartree-Fock-Slater local exchange approximation and relativistic wave functions.

^f

Lawrence (1967): uses an intermediate coupling theory.