2 Method

 

 

Table 1: The $\lambda$ parameters for Fe XXI

$n\ell$	$\lambda_{n\ell}$	$n\ell$	$\lambda_{n\ell}$
1s	1.43161	3s	1.28949
2s	1.43035	3p	1.23930
2p	1.34480	3d	1.37441

The method is described in detail in the first paper in the series (Hummer et al. [1993]). A brief summary is provided here together with data relevant to the assessment of the accuracy of the present calculation.

The electron + target scattering problem was solved using the close-coupling method in a Breit-Pauli approximation. The configuration interaction target wavefunctions were obtained using the program SUPERSTRUCTURE (Eissner et al. [1974]) in a version due to Nussbaumer & Storey ([1978]). The latter provides for more flexibility in the wavefunctions through the possible use of Coulomb functions and individual free parameters for the one-electron orbitals. The present target incorporated the following configurations:

2s22p2	2s2p3	2p4
2s22p3s	2s22p3p	2s22p3d
2s2p23s	2s2p23p	2s2p23d
2p33s	2p33p	2p33d

although only the first six configurations and a few of the 2s2p²3s states that are energetically lower than the higher lying 2s²2p3d levels appear explicitly in the current computation. This leads to a 28-term LS-coupling and a 52-level intermediate coupling target. Of course, the neglect of the other configurations has consequences for the accuracy to be expected.

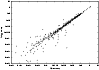Figure 1: Comparison of the f-values obtained in the present Fe XXI target calculation with those of Aggarwal et al. ([1997])

 

 

Table 2: Calculated versus observed (Corliss & Sugar [1982]) target energies (cm^-1)

Index	Term		$E_{{\rm calc}}$	$E_{{\rm obs}}$
1	2s22p2	3P $^{\rm e}_0$	0	0.0
2	2s22p2	3P $^{\rm e}_1$	82342	73850
3	2s22p2	3P $^{\rm e}_2$	131240	117353
4	2s22p2	1D $^{\rm e}_2$	266159	244560
5	2s22p2	1P $^{\rm e}_0$	392420	371900
6	2s2p3	5S$^\circ _2$	492100	486950
7	2s2p3	3D$^\circ _1$	788117	776780
8	2s2p3	3D$^\circ _2$	790592	777350
9	2s2p3	3D$^\circ _3$	824580	803930
10	2s2p3	3P$^\circ_0$	933542	916380
11	2s2p3	3P$^\circ _1$	945013	924880
12	2s2p3	3P$^\circ _2$	966608	942320
13	2s2p3	3S$^\circ _1$	1115277	1095600
14	2s2p3	1D$^\circ _2$	1156183	1126800
15	2s2p3	1P$^\circ _1$	1293363	1261000
16	2p4	3P $^{\rm e}_2$	1667455	1646300
17	2p4	3P $^{\rm e}_0$	1761165	1735700
18	2p4	3P $^{\rm e}_1$	1770134	1740500
19	2p4	1D $^{\rm e}_2$	1853211	1817300
20	2p4	1S $^{\rm e}_0$	2091087	2048200
21	2s22p3s	3P$^\circ_0$	7687260
22	2s22p3s	3P$^\circ _1$	7696818
23	2s22p3s	3P$^\circ _2$	7811152
24	2s22p3s	1P$^\circ _1$	7836056
25	2s22p3p	3D $^{\rm e}_1$	7864901
26	2s22p3p	3P $^{\rm e}_1$	7922276
27	2s22p3p	3D $^{\rm e}_2$	7926976
28	2s22p3p	3P $^{\rm e}_0$	7937875
29	2s22p3p	1P $^{\rm e}_1$	8012716
30	2s22p3p	3D $^{\rm e}_3$	8025472
31	2s22p3p	3S $^{\rm e}_1$	8034786
32	2s22p3p	1D $^{\rm e}_2$	8037228
33	2s2p23s	5P $^{\rm e}_1$	8094750
34	2s22p3p	3P $^{\rm e}_2$	8101009
35	2s22p3d	3F$^\circ _2$	8103486
36	2s22p3d	3F$^\circ _3$	8143904	8101400
37	2s22p3d	1D$^\circ _2$	8149622	8098000
38	2s2p23s	5P $^{\rm e}_2$	8150261
39	2s22p3p	1S $^{\rm e}_0$	8157038
40	2s22p3d	3D$^\circ _1$	8166771
41	2s2p23s	3P $^{\rm e}_0$	8204657
42	2s2p23s	5P $^{\rm e}_3$	8205472
43	2s22p3d	3F$^\circ_4$	8235261
44	2s22p3d	3D$^\circ _2$	8241715	8187400
45	2s2p23s	3P $^{\rm e}_1$	8244042
46	2s22p3d	3D$^\circ _3$	8264769	8195000
47	2s22p3d	3P$^\circ _1$	8275594
48	2s22p3d	3P$^\circ _2$	8279138	8230900
49	2s22p3d	3P$^\circ_0$	8284450
50	2s2p23s	3P $^{\rm e}_2$	8302380
51	2s22p3d	1F$^\circ _3$	8338459	8313600
52	2s22p3d	1P$^\circ _1$	8339760	8293900

 

 

Table 4: Transition probabilities for 2s²2p² - 2s2p³lines from this work and that of Froese Fischer & Saha ([1985])

Upper	Lower	This work	FFS
5S$^\circ _2$	3P $^{\rm e}_1$	4.210E+07	3.560E+07
5S$^\circ _2$	3P $^{\rm e}_2$	3.625E+07	3.272E+07
5S$^\circ _2$	1D $^{\rm e}_2$	1.343E+06	8.548E+05
3D$^\circ _1$	3P $^{\rm e}_0$	1.257E+10	1.191E+10
3D$^\circ _1$	3P $^{\rm e}_1$	6.485E+08	7.490E+08
3D$^\circ _1$	3P $^{\rm e}_2$	1.027E+08	6.727E+07
3D$^\circ _1$	1D $^{\rm e}_2$	2.000E+08	1.869E+08
3D$^\circ _1$	1P $^{\rm e}_0$	4.293E+07	4.191E+07
3D$^\circ _2$	3P $^{\rm e}_1$	9.636E+09	9.498E+09
3D$^\circ _2$	3P $^{\rm e}_2$	2.035E+07	5.570E+06
3D$^\circ _2$	1D $^{\rm e}_2$	3.841E+07	3.612E+07
3D$^\circ _3$	3P $^{\rm e}_2$	6.275E+09	6.472E+09
3D$^\circ _3$	1D $^{\rm e}_2$	1.060E+09	7.912E+08
3P$^\circ_0$	3P $^{\rm e}_1$	2.309E+10	2.254E+10
3P$^\circ _1$	3P $^{\rm e}_0$	4.301E+09	4.248E+09
3P$^\circ _1$	3P $^{\rm e}_1$	1.770E+10	1.642E+10
3P$^\circ _1$	3P $^{\rm e}_2$	2.515E+09	2.838E+09
3P$^\circ _1$	1D $^{\rm e}_2$	2.316E+08	1.959E+08
3P$^\circ _1$	1P $^{\rm e}_0$	1.640E+08	1.509E+08
3P$^\circ _2$	3P $^{\rm e}_1$	2.968E+08	3.791E+08
3P$^\circ _2$	3P $^{\rm e}_2$	2.177E+10	2.078E+10
3P$^\circ _2$	1D $^{\rm e}_2$	1.335E+08	5.708E+07
3S$^\circ _1$	3P $^{\rm e}_0$	9.560E+09	9.311E+09
3S$^\circ _1$	3P $^{\rm e}_1$	2.547E+10	2.538E+10
3S$^\circ _1$	3P $^{\rm e}_2$	6.306E+10	5.799E+10
3S$^\circ _1$	1D $^{\rm e}_2$	4.072E+08	9.426E+07
3S$^\circ _1$	1P $^{\rm e}_0$	7.092E+08	6.489E+08
1D$^\circ _2$	3P $^{\rm e}_1$	4.658E+08	3.953E+08
1D$^\circ _2$	3P $^{\rm e}_2$	8.651E+09	6.413E+09
1D$^\circ _2$	1D $^{\rm e}_2$	4.602E+10	4.626E+10
1P$^\circ _1$	3P $^{\rm e}_0$	2.943E+07	3.573E+07
1P$^\circ _1$	3P $^{\rm e}_1$	5.294E+09	5.963E+09
1P$^\circ _1$	1D $^{\rm e}_2$	6.888E+10	6.641E+10
1P$^\circ _1$	1P $^{\rm e}_0$	1.799E+10	1.753E+10

All orbitals have been made spectroscopic to avoid possible problems with pseudoresonances. The free parameters in the Thomas-Fermi-Dirac-Amaldi potential, $\lambda_{n\ell}$, obtained on minimizing the weighted sum of all the target energies are given in Table 1 while the calculated energies are compared with those observed (Corliss & Sugar [1982]) in Table 2. The energies are in some cases not as accurate as those obtained by Mason et al. ([1979]) or Aggarwal ([1991]) as no correlation configurations have been included while many more spectroscopic states have been incorporated.

The calculated oscillator strengths may also indicate the quality of the target wavefunctions. In Fig. 1 we compare oscillator strengths in the length approximation with those of Aggarwal et al. ([1997]) who used the CIV3 configuration-interaction program of Hibbert ([1975]). The figure clearly demonstrates that there are no major inconsistencies between the two datasets and that the overall agreement is excellent. This is in sharp contrast to the earlier f-values of Bhatia et al. ([1987]) who also used SUPERSTRUCTURE.

Froese Fischer & Saha ([1985]) performed detailed MCHF (Froese Fischer & Saha [1983]) calculations of the 2s²2p² - 2s2p³ transition probabilities for C-like ions. We compare these results with ours in Table 4. Again the overall agreement is excellent. It should be borne in mind that our energy levels are worst for these configurations so that the target as a whole is better than this comparison would indicate. The data on which Fig. 1 is based are tabulated in Table 3 which is only available in electronic form.

These target wavefunctions were then used to perform an R-matrix close-coupling calculation to determine the scattering states of the N+1electron system. An R-matrix package due to Eissner (unpublished) was used for this purpose. The asymptotic solutions, in particular the scattering matrices and consequently the collision strengths, were then obtained using the standard program suite described by Hummer et al. ([1993]). The use of 18 continuum orbitals in the scattering problem for each $\ell$ value leads to matrices of order 4500 and approximately 220 channels for each $J\pi$combination.

To ensure convergence in the total angular momentum values of J up to 59/2 were obtained. This is more than sufficient for the majority of transitions but for the allowed transitions and a few $J\rightarrow J$ among the n=2levels the values so obtained had to be "topped-up'' to account for the infinity of J values omitted from the summation. For the allowed transitions an implementation of the Coulomb-Bethe approximation due to Eissner (Eissner et al. [1999]) and based on the top-up procedure of Burke & Seaton ([1986]) for LS-coupling was available. For the slowly converging forbidden transitions a simple geometric progression was assumed but see the following section for further discussion of this point. The collision rates or effective collision strengths were obtained by integrating the collision strengths in the manner suggested by Burgess & Tully ([1992]) to ensure the proper behaviour at low temperatures.

Finally, the maximum total energy of 260 Ryd was insufficient to provide converged results at the highest temperatures so that the present results had to be extrapolated to higher energies. Here we have simply assumed the collision strength to be constant. Of course, this is not a good approximation but at 10⁷K this high-energy correction is never more than 10% of the total for any given cross section and hence the error is well within the bounds of other systematic errors. It does, however, mean that the present results should not be extrapolated to higher temperatures without paying careful attention to this point. Since the present results cover the maximum of the Fe²⁰⁺ ionization balance determined by Arnaud & Rothenflug ([1985]), this should not be necessary.

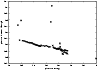Figure 2: The 2s22p2 3P $^{\rm e}_2\,-\,2$s2p3 3D$^\circ _3$collision strength with (filled circles) and without (x) top-up. Note that the data with top-up converge to the correct limit

Figure 3: The 2s22p2 3P $^{\rm e}_1 \,-\, ^3$P $^{\rm e}_2$collision strength at low energies. Comparison with Aggarwal's ([1991]) Fig. 1 shows good agreement with a cross section obtained in a Dirac approximation

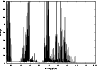Figure 4: The 2s22p2 3P $^{\rm e}_1 \,-\, ^3$P $^{\rm e}_2$collision strength at high energies. These resonances do not appear in the Aggarwal ([1991]) calculation

Figure 5: The 2s22p2 1D $^{\rm e}_2$ - 2s2p3 3D$^\circ _2$collision strength at low energies. Comparison with Aggarwal's ([1991]) Fig. 2 shows good agreement with a cross section obtained in a Dirac approximation

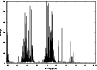Figure 6: The 2s22p2 1D $^{\rm e}_2\,-\,2$s2p3 3D$^\circ _2$collision strength at high energies. These resonances have been omitted from the Aggarwal ([1991]) calculation

Figure 7: The individual J contributions to the 2s22p2 3P $^{\rm e}_0$ - 2s2p3 5S$^\circ _2$ forbidden transition at an energy of 118 Ryd. The convergence is rapid

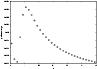Figure 8: The individual J contributions to the 2s22p2 3P $^{\rm e}_0 \,-\, 2$s2p3 3D$^\circ _1$ allowed transition at an energy of 118 Ryd. Note the long tail and corresponding slow convergence

Figure 9: The individual J contributions to the 2s2p3 5S $^\circ _2 - 2$s2p3 3P$^\circ _2$ forbidden transition at an energy of 118 Ryd. The convergence is slow (compare with Fig. 7)

Figure 10: The effective collision strength plotted as a function of temperature for the 2s22p2 3P $^{\rm e}_0 \,-\,$2s2 2p21D $^{\rm e}_2$ forbidden transition. The solid curve are the present results, dashed are from Aggarwal ([1991]). The contribution of the higher lying resonances is apparent

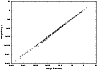Figure 11: Collision strengths from the present work compared with those of Zhang & Sampson ([1996]) at an ejected electron energy of 95.3 Ryd

Figure 12: Collision strengths from the present work compared with those of Zhang & Sampson ([1997]) at an ejected electron energy of 57.2 Ryd