3 Proper motion reduction and membership probability estimation

For the reduction of the proper motions we used the catalogue of positions and proper motions of 82 stars based on Hipparcos system given by Geffert et al. (1997) reduced from positions of stars on plates taken with the 30 cm refractor (f=5130 mm) over 60 years (Brosche et al. 1985). The catalogue is in the J2000 system with an epoch of 1950. It has 54 stars in common with the present work. These stars served as reference stars. A Central overlapping procedure (Russell 1976; Wang et al. 1996) was used for the proper motion reduction. The four B passband second epoch CCD frames were treated in the same way as the three first epoch plates and all will be designated as "plates" hereafter. The x,y coordinates of the stellar images in the plates with units of CCD pixel were multiplied by a suitable factor in order to convert them into numbers in units of mm, which are close to the units of the measurements of the first epoch plates. All of the 54 reference stars were adjusted in each iteration of position and proper motion reduction.

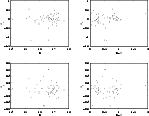
Figure 1: Plate CL 58004: residuals in X and Y vs. mag and color

Figure 2: CCD frame: residuals in X and Y vs. mag and color

Figure 3: $\mu_{\alpha}\cos\delta$ vs. RA, DEC., mag and color

Figure 4: $\mu _{\delta }$ vs. RA, DEC., mag and color

In the reduction we checked the need for different plate constants. It is shown that six plate constants would be enough for our central overlap procedure. Thus, higher order polynomials of the positions and additional magnitude and color terms were not necessary. Figure 1 gives the residuals in x and y with respect to magnitude and color, respectively, for plate CL 58004 (here we selected only stars which were seen on at least two of the first epoch plates), Fig. 2 gives the same relations for CCD frame 25m4147b30f. Both figures show no significant systematic trend. From these two figures one can find that the positional accuracy of the CCD frames is about 0 $^{\prime\prime}_{\raisebox{.6ex}{\hspace{.12em}.}}$13, which is consistent with our estimation above, while the positional accuracy for photographic plates is about 0 $^{\prime\prime}_{\raisebox{.6ex}{\hspace{.12em}.}}$20 (after rejecting several stars with large deviations).

After the fourth iteration positions and proper motions from two subsequent iteration steps showed little deviations. Mean differences in position were smaller than 0 $^{\prime\prime}_{\raisebox{.6ex}{\hspace{.12em}.}}$03, the rms is smaller than 6 mas and the differences in proper motion were below 1 mas/yr, the rms below 0.15 mas/yr. We took the positions and proper motions of 115 stars given by this iteration as the final outcome and their errors are listed in Table 6. It should be pointed out that the errors given in Table 6 are only estimates of internal errors in the adjustment process and are undoubtedly underestimated to some extent. In our following discussion on the membership probabilities, we shall give more realistic error estimates.

   

Table 6: Internal astrometric errors

Parameter	Median error	Maximum error
$\alpha$	$0\hbox{$.\!\!^{\rm s}$ }0041$	$0\hbox{$.\!\!^{\rm s}$ }0394$
$\delta$	$0\hbox{$.\!\!^{\prime\prime}$ }059$	$0\hbox{$.\!\!^{\prime\prime}$ }404$
$\mu_{\alpha}\cos\delta$	1.45 mas/yr	15.13 mas/yr
$\mu _{\delta }$	1.39 mas/yr	11.88 mas/yr

To search for possible systematic errors in our resulting proper motions, we selected a test sample of 34 stars with membership probabilities greater than 0.7 and of horizontal branch or the giant branch nature from the V versus (V-I) diagram (see Fig. 6 and text below). From this sample, the resulting proper motions were plotted against R.A., DEC., V and V-I, respectively, as is shown in Fig. 3 and Fig. 4. No apparent systematic dependence could be found in these figures. However, as is seen in these figures, the proper motion dispersions are much greater than the internal errors in Table 6. The proper motion dispersions here are 2.7 mas/yr in right ascension and 3.2 mas/yr in declination, respectively, which should be related to the astrometric accuracy of the CCD frames and the photographic plates. For those stars which are seen on all three plates and four CCD frames, the accuracy is rather 3 mas/yr.

For the membership probability estimation, we used a maximum likelihood method with a 9-parameter Gaussian model as follows:

$$\begin{eqnarray*}\Phi(\mu_{xi},\mu_{yi}) & {=} & \Phi_{\rm c}(\mu_{xi},\mu_{yi})... ...yf})^{2}}{\sigma^{2}_{y0}+\varepsilon^{2}_{yi}}\right]\right\}. \end{eqnarray*}$$

where $(\mu_{xi},\mu_{yi})$ and $(\varepsilon_{xi},\varepsilon_{yi})$ are the proper motion components of the i-th star and their observing errors, respectively. The centers of the cluster and of the field stars in the proper motion vector point diagram, $(\mu_{x{\rm c}},\mu_{y{\rm c}})$ and $(\mu_{x{\rm f}},\mu_{y{\rm f}})$, the intrinsic dispersions of the proper motions of the cluster members and field stars $\sigma_{0}$ and $(\sigma_{x0},\sigma_{y0})$, the correlation coefficient $\rho$, and $n_{\rm c}$, the fraction of all member stars, have to be determined in the fit. The 9 parameters were determined by the maximum likelihood procedure and their uncertainties by the second derivative of the likelihood function. The results are summarized in Table 7. Once these parameters are determined, the membership probability of i-th star is given by

$$p_{i}=\Phi_{\rm c}(\mu_{xi},\mu_{yi})/\Phi(\mu_{xi},\mu_{yi}) .$$

Figure 5 gives the vector point plot diagram of the 115 stars, with different symbols for different probabilities. The number of stars with different membership probabilities is shown in Table 8. According to the value of $n_{\rm c}$ in Table 7, there should be 70 cluster stars, under the assumption that stars with $p\le 0.6$ can be regarded as field stars.

Figure 5: Vector point diagram of proper motions

   

Table 7: Estimates of model parameters from maximum likelihood fitting

Parameter	Estimate
$\mu_{x{\rm c}}$	-1.65 $\pm$ 0.39 mas/yr
$\mu_{y{\rm c}}$	-2.69 $\pm$ 0.38 mas/yr
$\mu_{x{\rm f}}$	-5.30 $\pm$ 0.66 mas/yr
$\mu_{y{\rm f}}$	-4.13 $\pm$ 2.63 mas/yr
$\sigma_{\rm o}$	2.58 $\pm$ 0.33 mas/yr
$\sigma_{x_{\rm o}}$	12.69 $\pm$ 0.10 mas/yr
$\sigma_{y_{\rm o}}$	11.52 $\pm$ 1.40 mas/yr
$\rho$	-0.105 $\pm$ 0.095
$n_{\rm c}$	0.698 $\pm$ 0.051

   

Table 8: Membership probability distribution of stars in the region of NGC 4147

Prob.	Number of stars
1.00-0.90	59
0.90-0.80	16
0.80-0.70	6
0.70-0.60	2
0.60-0.50	2
0.50-0.40	2
0.40-0.30	1
0.30-0.20	2
0.20-0.10	3
0.10-0.01	3
0.00	19

The values in Table 7 provide a possibility of estimating the external accuracy of the proper motion results in this work. Since NGC 4147 is very far away from us the contribution by the internal motions of the cluster stars can be neglected and $\sigma_{0}$ can be regarded entirely as the observational dispersion. The dispersion of 2.6 mas/yr is in good agreement with the error estimated from the astrometric accuracy of the CCD frames and the plates.