The internal errors of the instrumental (non-calibrated) magnitudes and
those
of the particular SB profile are dominated by the error of the adopted
sky background value and includes, in addition, the random count
error in aperture measurements. The smooth sky background level at the
position of the (masked) galaxies was computed (within PIPS)
by means of an iterative filtering process
which produces a minimum surface between the surrounding
background of every particular masked object. That means, the computed
sky level depends on local SB fluctuations.
We measured the sky background
fluctuations on the filtered CCD frames by means of small apertures in the
vicinity of the studied galaxies. For the 600 s B exposures
(and 300 s R exposures) the sky background fluctuations are
typically 0.2 percent. For the snap-shot 60 s exposures the
corresponding fluctuations are 0.4 - 0.8 percent in B and
0.5 percent in R. Thus, the SB profiles are sky background
limited at
![]() 27.5 B mag/
27.5 B mag/
![]() for typical 60 s
exposures and can be traced down to
for typical 60 s
exposures and can be traced down to
![]() 28.5 B mag/
28.5 B mag/
![]() on the deepest (900 s) frames. Beyond the given limits the error in the
mean sky begins to exceed the signal from the object.
Following Vader & Chaboyer ([1994]) we calculated
the internal errors in intensity as
on the deepest (900 s) frames. Beyond the given limits the error in the
mean sky begins to exceed the signal from the object.
Following Vader & Chaboyer ([1994]) we calculated
the internal errors in intensity as
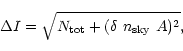 |
(3) |
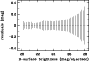 |
Figure 2:
The 1 |
In order to evaluate the true magnitude calibration errors we compared
our total magnitude measurements with the available published data, as
quoted in NASA/IPAC Extragalactic Database (NED). There are very few
reliable photometric data available in the literature for the studied
ELGs. For two galaxies, namely HS 1311+3628 (UGC 8303) and
HS 1312+3508 (UGC 8323), the ![]() magnitudes are given in RC3
(de Vaucouleurs et al. [1991]). For four further galaxies,
(HS 1331+3906, HS 1336+3114, HS 1400+3927
and HS 1402+3657) total
magnitudes have been listed by Garnier et al. ([1996]), with typical
uncertainties of about 0.5 mag. For the HS 1400+3927 our total
brightness is about 1 mag fainter than the one quoted by
Garnier et al. ([1996]). The reason of this rather large difference
is unclear. The remaining five common galaxies show reasonably
small magnitude residuals with a mean value of
magnitudes are given in RC3
(de Vaucouleurs et al. [1991]). For four further galaxies,
(HS 1331+3906, HS 1336+3114, HS 1400+3927
and HS 1402+3657) total
magnitudes have been listed by Garnier et al. ([1996]), with typical
uncertainties of about 0.5 mag. For the HS 1400+3927 our total
brightness is about 1 mag fainter than the one quoted by
Garnier et al. ([1996]). The reason of this rather large difference
is unclear. The remaining five common galaxies show reasonably
small magnitude residuals with a mean value of
![]() = +0.17 mag, and an 1
= +0.17 mag, and an 1![]() dispersion of 0.21
mag.
dispersion of 0.21
mag.
Available B-magnitudes of the studied ELGs were collected by Popescu et al.
([1996], Table 4, (![]() ,
Col. 7)) from various literature sources.
The mean accuracy of these heterogeneous data was estimated to be
of
,
Col. 7)) from various literature sources.
The mean accuracy of these heterogeneous data was estimated to be
of ![]() 0.5 mag.
In Fig. 3 we compare these magnitudes with our data (open circles on
the plot), for 22 ELGs in common with our sample. The dispersion of
individual values is large (1
0.5 mag.
In Fig. 3 we compare these magnitudes with our data (open circles on
the plot), for 22 ELGs in common with our sample. The dispersion of
individual values is large (1![]() = 0.78 mag). However the mean
value of the magnitude residuals,
= 0.78 mag). However the mean
value of the magnitude residuals,
![]() =
+0.26
=
+0.26 ![]() 0.16, is in agreement with the accuracy of the literature
data,
0.16, is in agreement with the accuracy of the literature
data, ![]() ,
and no systematic trend is evident.
,
and no systematic trend is evident.
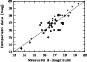 |
Figure 3:
Comparison of our measured B-magnitudes with the data
obtained from literature: our |
Further we compare our isophotal magnitudes (B25) with the photographic
m24.5 magnitudes measured by Odewahn & Alderding ([1995]) on the
blue 103a-O plates (Fig. 3, crosses).
Our B25 magnitudes are systematically more luminous:
![]() = -0.42
= -0.42 ![]() 0.06, as could be expected because of
the limiting isophote differences. However, the dispersion of
individual data points is reasonably small (1
0.06, as could be expected because of
the limiting isophote differences. However, the dispersion of
individual data points is reasonably small (1![]() = 0.25),
and no systematic trend is evident within the given magnitude
interval. As a result of these comparisons we estimate the accuracy
of our isophotal and total B-magnitudes to be not worse than
= 0.25),
and no systematic trend is evident within the given magnitude
interval. As a result of these comparisons we estimate the accuracy
of our isophotal and total B-magnitudes to be not worse than ![]() 0.2
mag.
0.2
mag.
For the R-magnitudes there are no comparison data available in the
literature, except the photographic
![]() magnitudes
measured by Odewahn & Alderding ([1995]) on the red 103a-E plates. In
Fig. 4 our total colour indices (
magnitudes
measured by Odewahn & Alderding ([1995]) on the red 103a-E plates. In
Fig. 4 our total colour indices (
![]() )
are plotted versus
)
are plotted versus
![]() ).
Since the mean colour of ELGs is
).
Since the mean colour of ELGs is
![]() 0.9, the
photographic
0.9, the
photographic
![]() and
and
![]() magnitudes of common
galaxies should refer to nearly the same aperture. Rejecting one
single discordant photographic colour value of
magnitudes of common
galaxies should refer to nearly the same aperture. Rejecting one
single discordant photographic colour value of
![]() = 2.34 for HS 1325+3255, the remaining 10
common galaxies show that our measured colours are systematically
bluer by about 0.13 mag than the photographic colours (1
= 2.34 for HS 1325+3255, the remaining 10
common galaxies show that our measured colours are systematically
bluer by about 0.13 mag than the photographic colours (1![]() dispersion of 0.21 mag). The given systematics in the colour
indices is probably mainly caused by differences in the CCD and
photographic magnitude systems.
dispersion of 0.21 mag). The given systematics in the colour
indices is probably mainly caused by differences in the CCD and
photographic magnitude systems.
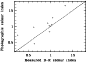 |
Figure 4: Comparison of our measured total (B-R) colour indices with photographic colours from Odewahn & Alderding ([1995]) |
Copyright The European Southern Observatory (ESO)