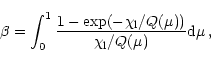Appendix B: Simple approximation for the escape probability

In the Sobolev approximation, the escape probability for a line photon in the spherically symmetric accelerating outflow is given by (See e.g. Mihalas [1978], Sect. 14.2)

$$\beta=\int_0^1\frac{1-\exp(-\chi_{\mathrm l}/Q(\mu))} {\chi_{\mathrm l}/Q(\mu)} {\mathrm d}\mu\,,$$ (B1)

where

$$Q(\mu)=\mu^2\partial{V}/\partial{r}+(1-\mu^2)(V/r)\,,$$

$$\chi_{\mathrm l}=\frac{(\pi e^2/mc)f}{\Delta\nu_{\rm D}}n\,,$$

$V=v/v_{\rm th}$, v and $v_{\rm th}$ are the outflow and scattering atoms thermal velocities respectively, we set $\Delta\nu_{\rm D}=\nu v_{\rm th}/c$, $\nu$ is the line frequency, f is the oscillator strength, and n is the number density of atoms on the lower level of the transition.

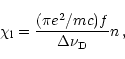
Here and in what follows we consider the fixed point of the envelope at the distance r from the center and do not show explicitly the dependence of $\beta$, V, n, and other physical parameters of the envelope on r. Also, in expression for $\chi_{\rm l}$ we neglected the stimulated emission, which do not introduce a noticeable error when the formation of H$\alpha$ in the P Cyg envelope is considered.

Our purpose is to find an approximation $\tilde\beta$ to $\beta$ that permits fast evaluation. By solving the equations of statistical equilibrium using the approximation instead of the exact definition, $\tilde\beta$ should retain principal mathematical properties of $\beta$ reflecting the underlying physics. Namely, we require that $\tilde\beta(0)=1$ and $\tilde\beta(n)$ should monotonically decrease to zero as $n\to\infty$.

The simplest function that obeys the above stated requirements is

$$\tilde\beta=\frac{1}{1+n/n_{\mathrm{as}}}\,,$$ (B2)

where $n_{\rm {as}}$ is a parameter. To choose the optimal value of $n_{\rm {as}}$, we consider the behavior of $\beta(n)$ for large n. When $n\to\infty$, the numerator of the integrand in Eq. (B1) can be replaced by 1 and an asymptotic form of $\beta$ can be easily computed.

Comparison of that asymptotic form with Eq. (B2) shows that if we set

$$n_{\mathrm{as}}= 8\pi\frac{g_{\mathrm l}}{g_{\mathrm u}}\fra... ...}{3}\frac{{\rm d}v}{{\rm d}r}+\frac{2}{3}\frac{v}{r}\right)\,,$$ (B3)

then $\tilde\beta/\beta=1$ up to the terms of order 1/n when $n\to\infty$. Here $g_{\rm l}$ and $g_{\rm u}$ are statistical weights of the lower and upper levels of the transition respectively, $\lambda$ is the line wavelength, and $A_{\rm ul}$ is the spontaneous emission coefficient.

To study the precision of approximation (B2), we performed numerical computations for a wide range of values $({\rm d}v/{\rm d}r)/(v/r)$ and $n/n_{{\rm as}}$ (it can be easily shown that the error is uniquely determined by the values of these two parameters). Our results show that the relative error reaches its maximum of 0.23 for $\frac{{\rm d}v(r)}{{\rm d}r}=\frac{v(r)}{r}$, that is when $v(r)\propto r$, and $n_2/n_{{\rm as}}\approx1.8$.

The approximation found here is applicable if the escape probability is given by Eq. (B1), that is if the frequency change in scattering is described by complete frequency redistribution. Of course, this is useful only if the usual conditions of applicability of the Sobolev approximation are satisfied. The expressions (B2) and (B3) can be generalized in two ways. First, the error can be reduced if rational approximations of higher order are used instead of Eq. (B2). Second, a similar approximation can be obtained for a general three-dimensional flow as will be showed in a future study.