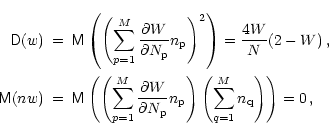Up: Relative figure of merit
Appendix A: Computation of Dwi
and M(niwi)
In this Appendix, we compute the non-trivial elements of the
covariance matrix of errors used in Sect. 3.2.
Since we consider here a single spectral channel, the index iwill be omitted everywhere. Thus, the values N, 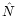 ,
n, W,
,
n, W,
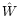 ,
and w in this Appendix are identical with the values
denoted as Ni,
,
and w in this Appendix are identical with the values
denoted as Ni, 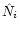 ,
ni, Wi,
,
ni, Wi,
 ,
and wi respectively in Sect. 2.
,
and wi respectively in Sect. 2.
In practice, the error in 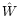 depends on too many details of
experimental techniques, atmospheric conditions and data processing
methods to be analyzed in general form (Mourard et al. [1994]).
The present analysis is restricted to a highly idealized situation.
Namely, as well as in Sect. 3.1, the only source of
measurement errors taken into account is the photon shot noise. We
assume that the static fringes are detected by counting the photons in
nonintersecting channels that cover in total the interval of length
Z of optical path difference (OPD).
If z is the OPD, which is measured here in units of
depends on too many details of
experimental techniques, atmospheric conditions and data processing
methods to be analyzed in general form (Mourard et al. [1994]).
The present analysis is restricted to a highly idealized situation.
Namely, as well as in Sect. 3.1, the only source of
measurement errors taken into account is the photon shot noise. We
assume that the static fringes are detected by counting the photons in
nonintersecting channels that cover in total the interval of length
Z of optical path difference (OPD).
If z is the OPD, which is measured here in units of
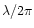 ,
and
F(z) is the photon counting rate per unit z, then
,
and
F(z) is the photon counting rate per unit z, then
 |
(A1) |
where z0 is unknown fringe phase shift and
N is proportional to the total received flux.
If we define
 |
(A2) |
and
 |
(A3) |
then assuming that 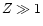 and neglecting the
terms that decrease as 1/Z for
and neglecting the
terms that decrease as 1/Z for
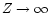 we obtain that
we obtain that
 |
(A4) |
and
 |
(A5) |
An estimate for W=V2 can be constructed by replacing the values in
the RHS of Eq. (A5) by their estimates that can be easily
deduced from Eqs. (A2)-(A4). If the interval of
OPDs covered by measurements is divided in M subintervals of
length
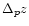 and
and
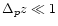 for
for
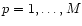 ,
then
an estimate
,
then
an estimate 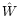 of W based upon the number of photons received
in each of these subintervals is given by
of W based upon the number of photons received
in each of these subintervals is given by
where
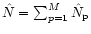 ,
,
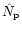 is the number of photons received in the
p-th subinterval,
is the number of photons received in the
p-th subinterval,
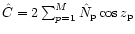 ,
and
,
and
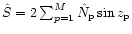 .
.
If we assume further that
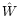 as a function of
as a function of
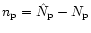 can be linearized in the vicinity of zero and take into account that
can be linearized in the vicinity of zero and take into account that
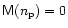 and
and
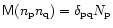 ,
then after some algebra we obtain for the statistical
characteristics of
,
then after some algebra we obtain for the statistical
characteristics of 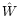
which proves the validity of Eqs. (15) and (16)
for i=j.


Up: Relative figure of merit
Copyright The European Southern Observatory (ESO)
![]() depends on too many details of
experimental techniques, atmospheric conditions and data processing
methods to be analyzed in general form (Mourard et al. [1994]).
The present analysis is restricted to a highly idealized situation.
Namely, as well as in Sect. 3.1, the only source of
measurement errors taken into account is the photon shot noise. We
assume that the static fringes are detected by counting the photons in
nonintersecting channels that cover in total the interval of length
Z of optical path difference (OPD).
If z is the OPD, which is measured here in units of
depends on too many details of
experimental techniques, atmospheric conditions and data processing
methods to be analyzed in general form (Mourard et al. [1994]).
The present analysis is restricted to a highly idealized situation.
Namely, as well as in Sect. 3.1, the only source of
measurement errors taken into account is the photon shot noise. We
assume that the static fringes are detected by counting the photons in
nonintersecting channels that cover in total the interval of length
Z of optical path difference (OPD).
If z is the OPD, which is measured here in units of
![]() ,
and
F(z) is the photon counting rate per unit z, then
,
and
F(z) is the photon counting rate per unit z, then
![]() as a function of
as a function of
![]() can be linearized in the vicinity of zero and take into account that
can be linearized in the vicinity of zero and take into account that
![]() and
and
![]() ,
then after some algebra we obtain for the statistical
characteristics of
,
then after some algebra we obtain for the statistical
characteristics of ![]()