

Up: Relative figure of merit
Subsections
5 Results
In total, the values
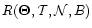 and
and
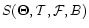 were calculated as a function
of projected baseline length for various sets of target and
nuisance parameters at
more than 105 points of the parametric space. Table 1
presents the principal characteristics of the model grids. The ranges
of variations of model parameters on the grids were chosen so as to
include the values of parameters from earlier works on P Cyg
cited in Sect. 4.1.
were calculated as a function
of projected baseline length for various sets of target and
nuisance parameters at
more than 105 points of the parametric space. Table 1
presents the principal characteristics of the model grids. The ranges
of variations of model parameters on the grids were chosen so as to
include the values of parameters from earlier works on P Cyg
cited in Sect. 4.1.
Table 1:
Grids of models: the number of points in the
parametric space 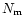 ;
dimension, that is the number of varied parameters, of the grid
D;
the values of parameters that were fixed on the grid; and the
ranges of variation for variable parameters
;
dimension, that is the number of varied parameters, of the grid
D;
the values of parameters that were fixed on the grid; and the
ranges of variation for variable parameters
|
Grid |
 |
D |
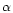 |
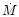 |
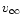 |
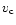 |
T1 |
R2 |
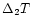 |
R3 |
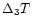 |
R4 |
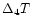 |
R5 |
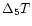 |
| no. |
|
|
|
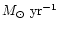 |
km s-1 |
km s-1 |
K |
|
K |
|
K |
|
K |
|
K |
|
1 |
10000 |
3 |
3.5 |
1.010-5 |
200 |
15.0 |
11000 |
|
|
|
|
|
|
|
|
| |
|
|
4.5 |
2.010-5 |
|
55.0 |
15000 |
|
|
|
|
|
|
|
|
2 |
10000 |
3 |
3.5 |
1.010-5 |
200 |
15.0 |
11000 |
2.0 |
1300 |
3.4 |
2100 |
5.0 |
200 |
10.0 |
3000 |
| |
|
|
4.5 |
2.010-5 |
|
55.0 |
15000 |
|
|
|
|
|
|
|
|
3 |
32805 |
4 |
3.5 |
1.010-5 |
150 |
15.0 |
11000 |
|
|
|
|
|
|
|
|
| |
|
|
4.5 |
2.010-5 |
250 |
55.0 |
15000 |
|
|
|
|
|
|
|
|
4 |
15625 |
6 |
3.5 |
1.010-5 |
200 |
15.0 |
11000 |
2.0 |
0 |
5.0 |
0 |
|
|
|
|
| |
|
|
4.5 |
2.010-5 |
|
55.0 |
15000 |
|
1300 |
|
2300 |
|
|
|
|
5 |
46656 |
6 |
3.25 |
1.010-5 |
200 |
15.0 |
11000 |
2.0 |
0 |
3.4 |
0 |
|
|
|
|
| |
|
|
4.25 |
2.010-5 |
|
55.0 |
15000 |
|
1300 |
|
2100 |
|
|
|
|
6 |
6561 |
8 |
3.5 |
1.010-5 |
200 |
15.0 |
11000 |
2.0 |
0 |
3.4 |
0 |
5.0 |
0 |
10.0 |
0 |
| |
|
|
4.5 |
2.010-5 |
|
55.0 |
15000 |
|
1300 |
|
2100 |
|
200 |
|
3000 |
7 |
65536 |
8 |
3.5 |
1.010-5 |
200 |
15.0 |
11000 |
2.0 |
0 |
3.0 |
0 |
4.0 |
0 |
5.0 |
0 |
| |
|
|
4.5 |
2.010-5 |
|
55.0 |
15000 |
|
1300 |
|
2100 |
|
200 |
|
3000 |
8 |
6561 |
8 |
4.0 |
1.510-5 |
180 |
20.0 |
14000 |
2.0 |
0 |
3.0 |
0 |
4.0 |
0 |
5.0 |
0 |
| |
|
|
4.5 |
2.310-5 |
220 |
|
16000 |
|
1000 |
|
1000 |
|
1000 |
|
1000 |
9 |
19683 |
9 |
3.5 |
1.510-5 |
220 |
15.0 |
16000 |
2.0 |
0 |
3.0 |
0 |
4.0 |
0 |
5.0 |
0 |
| |
|
|
4.5 |
2.310-5 |
300 |
25.0 |
18000 |
|
1300 |
|
2100 |
|
200 |
|
3000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The main result of the present study is that the increase in accuracy
provided by OLBI strongly depends on the number of free parameters in
the model: it varies from almost negligible for models of low
dimension to very significant for models of high dimension. Since
in our case the boundary between "low'' and "high'' is nearly
coincident with division into models with fixed and adjustable thermal
structure, we discuss the results pertaining to those two classes of
models separately.
Among our grids, the grid 1 most closely corresponds to the models
often used in interpreting H observations of P Cyg stars,
where
observations of P Cyg stars,
where
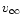 is excluded from the set of adjustable parameters
of the model (see e.g. Scuderi et al. [1994]) and its value
is taken from the analysis of absorption lines of metals in the
ultraviolet (Casatella et al. [1979]; Lamers et al.
[1985]).
is excluded from the set of adjustable parameters
of the model (see e.g. Scuderi et al. [1994]) and its value
is taken from the analysis of absorption lines of metals in the
ultraviolet (Casatella et al. [1979]; Lamers et al.
[1985]).
The typical results for an individual point in the parametric space
are illustrated by Fig. 1, where the random error ratio
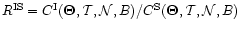 is plotted as a function of the normalized baseline length B/B0 for
various
is plotted as a function of the normalized baseline length B/B0 for
various
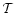 and
and
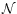 .
Here B is the projected
baseline length,
.
Here B is the projected
baseline length,
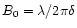 ,
and
,
and 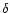 is the angular
radius of the central star. For the adopted values of
is the angular
radius of the central star. For the adopted values of
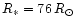 ,
,
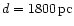 ,
and
,
and
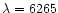 Å
one gets
Å
one gets
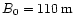 .
.
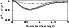 |
Figure 1:
Error ratio for isothermal model with
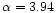 , ,
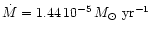 , ,
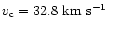 , ,
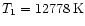 , ,
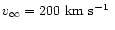 ,
and the set of adjustable parameters ,
and the set of adjustable parameters
 , ,
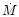 , ,
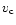 , ,
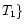 .
Target set .
Target set
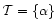 (solid line),
(solid line),
 (dashed line),
(dashed line),
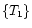 (short-dashed line), and
(short-dashed line), and
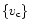 (dotted line)
(dotted line) |
The principal features of dependence of
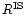 on B are
independent of details of the physical model used and can
be easily explained qualitatively. As shown in
Sect. 3.3, inequality
on B are
independent of details of the physical model used and can
be easily explained qualitatively. As shown in
Sect. 3.3, inequality
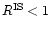 holds for all
holds for all
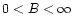 .
When the projected baseline length is very small,
the interferometry does not provide any additional information as
compared with the spectroscopy, for the object gets
unresolved. Consequently,
.
When the projected baseline length is very small,
the interferometry does not provide any additional information as
compared with the spectroscopy, for the object gets
unresolved. Consequently,
 for
for 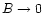 .
In
the opposite case of large B the fringe contrast is close to 0
for all physically realistic intensity distributions and its
dependence on model parameters is impossible to measure because of
observational errors. That is, in that case the interferometry
again provides no additional information and
.
In
the opposite case of large B the fringe contrast is close to 0
for all physically realistic intensity distributions and its
dependence on model parameters is impossible to measure because of
observational errors. That is, in that case the interferometry
again provides no additional information and
 for
for
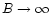 .
.
It follows from the
above stated general properties of
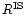 that for any
that for any
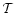 and
and
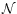 it has a (possibly non-unique)
minimum at a certain finite values of B. The location
of the minimum indicates the projected baseline length at which
interferometric observations are most informative, and the
corresponding value of
it has a (possibly non-unique)
minimum at a certain finite values of B. The location
of the minimum indicates the projected baseline length at which
interferometric observations are most informative, and the
corresponding value of
 characterize to what degree
the interferometry can reduce the errors in model parameters
determination as compared to spectroscopy.
characterize to what degree
the interferometry can reduce the errors in model parameters
determination as compared to spectroscopy.
Let us note that it may not be correct to compare the
merits of the methods using values of
 obtained for
an isolated point or even for a few arbitrarily chosen points of
parametric space. Since the model parameters are not known a
priori, it is necessary to use integral characteristics
describing the behaviour of
obtained for
an isolated point or even for a few arbitrarily chosen points of
parametric space. Since the model parameters are not known a
priori, it is necessary to use integral characteristics
describing the behaviour of
 on the whole grid. We
will use the following three values calculated as a function
of Bj/B0 for various
on the whole grid. We
will use the following three values calculated as a function
of Bj/B0 for various
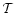 and
and
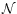 :
:
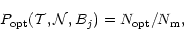 |
(26) |
where
 is the number of points on the grid for which
function
is the number of points on the grid for which
function
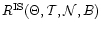 reaches its
minimum at B=Bj.
reaches its
minimum at B=Bj.
The function defined in Eq. (26)
is immediately related to the problem of optimal choice of the baseline
length: for given
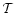 and
and
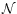 ,
the higher the
value
,
the higher the
value
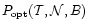 ,
the higher the
probability that the interferometric observations at the baseline length
B would yield the most accurate model parameters.
The dependence of
,
the higher the
probability that the interferometric observations at the baseline length
B would yield the most accurate model parameters.
The dependence of 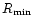 and
and
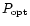 on the
normalized baseline length
and set of target parameters for grid 1 is shown in
Fig. 2. For this grid, the value of
on the
normalized baseline length
and set of target parameters for grid 1 is shown in
Fig. 2. For this grid, the value of 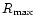 is
close to unity for all
is
close to unity for all
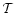 and
and
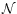 and is not shown
in the plot.
and is not shown
in the plot.
 |
Figure 2:
The lower limit of random error ratio 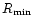 (solid line) and
distribution of optimal baseline lengths
(solid line) and
distribution of optimal baseline lengths
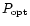 (dashed lines,
plotted in an arbitrary scale) for grid 1.
The set of adjustable parameters
(dashed lines,
plotted in an arbitrary scale) for grid 1.
The set of adjustable parameters
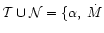 , ,
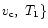 ,
target parameters are indicated on the plots ,
target parameters are indicated on the plots |
It can be easily seen that for this grid of models OLBI
provides only a relatively small reduction of the random error in parameter
determination as compared with spectroscopy. This conclusion remains
also valid if we add the terminal velocity
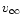 to the set
of adjustable parameters (grid 3).
to the set
of adjustable parameters (grid 3).
As
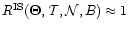 for
all
for
all
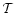 and
and
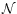 ,
the same approximate equality is
evidently valid for the robustness ratio
,
the same approximate equality is
evidently valid for the robustness ratio
 ,
which indicates (see
Sect. 2.3) that for models with a priori fixed thermal
structure, interferometric data will not reduce appreciably the
level of systematic errors.
,
which indicates (see
Sect. 2.3) that for models with a priori fixed thermal
structure, interferometric data will not reduce appreciably the
level of systematic errors.
The number of possible target sets is an exponentially increasing
function of the dimension D of the model parameter space, so that
when the values  are added to the set of unknowns, it
becomes impossible to make an exhaustive presentation of even the
integral results, i.e. the functions
are added to the set of unknowns, it
becomes impossible to make an exhaustive presentation of even the
integral results, i.e. the functions
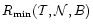 ,
,
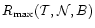 ,
and
,
and
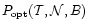 .
.
In Fig. 3, we show the dependence of 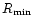 ,
,
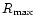 ,
and
,
and
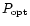 on
the number of nuisance parameters for one of our simplest grids of
models with adjustable thermal structure, the target set
consisting of one parameter, the mass loss rate
on
the number of nuisance parameters for one of our simplest grids of
models with adjustable thermal structure, the target set
consisting of one parameter, the mass loss rate 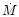 .
From many points
of view,
it is the most important parameter of the stellar wind, characterizing
both its effect on the evolution of the star and the influence of the
outflowing matter on the surrounding interstellar medium.
.
From many points
of view,
it is the most important parameter of the stellar wind, characterizing
both its effect on the evolution of the star and the influence of the
outflowing matter on the surrounding interstellar medium.
 |
Figure 3:
The lower and upper limits of random error ratio (solid lines,
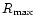 differs noticeably from unity only in the bottom plot) and
distribution of optimal baseline lengths
differs noticeably from unity only in the bottom plot) and
distribution of optimal baseline lengths
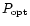 (dashed lines,
plotted in an arbitrary scale) for grid 5.
Target set
(dashed lines,
plotted in an arbitrary scale) for grid 5.
Target set
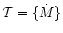 ,
nuisance parameters are indicated on the plots ,
nuisance parameters are indicated on the plots |
As it can be seen,
the lower limit of the random error ratio 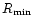 rapidly decreases as
the number of adjustable temperature parameters increases, so that
when the thermal structure of the envelope becomes a nuisance parameter,
interferometry can reduce the random error in
rapidly decreases as
the number of adjustable temperature parameters increases, so that
when the thermal structure of the envelope becomes a nuisance parameter,
interferometry can reduce the random error in 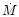 by as much as an
order of magnitude.
by as much as an
order of magnitude.
Note, that the decrease in 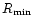 is caused by the fact that
parameters
is caused by the fact that
parameters  are adjustable, rather then by deviation from
isothermicity. This can be seen from the upper two plots in
Fig. 3, where
are adjustable, rather then by deviation from
isothermicity. This can be seen from the upper two plots in
Fig. 3, where
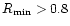 for a grid containing a high
proportion of models with a noticeable temperature gradient, and is also
supported by the results obtained for grid 2, which differs from
grid 1 only in that its thermal structure approximates that of Drew's
model B, which corresponds to
for a grid containing a high
proportion of models with a noticeable temperature gradient, and is also
supported by the results obtained for grid 2, which differs from
grid 1 only in that its thermal structure approximates that of Drew's
model B, which corresponds to 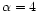 ,
,
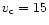 km s-1,
km s-1,
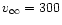 km s-1,
and
km s-1,
and
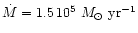 in our notations,
instead of being isothermal.
in our notations,
instead of being isothermal.
For other single-parameter target sets the dependencies of 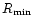 and
and 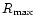 on
on
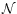 are qualitatively the same.
Figure 4 displays the results for the most important case when
all the parameters of the model except for
are qualitatively the same.
Figure 4 displays the results for the most important case when
all the parameters of the model except for
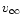 are
adjustable. As one can see, again, in favorable circumstances
interferometry can increase accuracy by an order of magnitude.
are
adjustable. As one can see, again, in favorable circumstances
interferometry can increase accuracy by an order of magnitude.
 |
Figure 4:
The lower and upper limits of random error ratio (solid lines) and
distribution of optimal baseline lengths
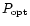 (dashed lines) for grid 5,
(dashed lines) for grid 5,
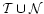 = =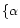 , ,
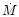 , ,
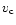 ,
T1, ,
T1, 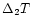 , ,
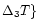 ,
and target sets indicated on the plots ,
and target sets indicated on the plots |
In contrast to 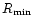 ,
the value
,
the value 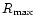 is close to unity for
all projected baseline lengths and combinations of sets
is close to unity for
all projected baseline lengths and combinations of sets
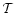 and
and
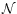 that we have studied. This signifies that for
any projected baselength there exists a combination of model
parameters for which interferometry practically do not provide
reduction in error.
that we have studied. This signifies that for
any projected baselength there exists a combination of model
parameters for which interferometry practically do not provide
reduction in error.
It is interesting to notice that for target sets containing several
parameters (see
Fig. 5), the influence of individual parameters on
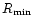 and
and 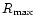 to some extent averages out:
to some extent averages out: 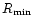 is systematically higher, and
is systematically higher, and 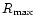 is systematically lower than
the corresponding values for individual parameters. For this reason,
when more than one model parameter is to be determined,
interferometry at a single projected baselength is unlikely to
yield overall gain in accuracy in excess of a factor of two even at
optimal baselines.
is systematically lower than
the corresponding values for individual parameters. For this reason,
when more than one model parameter is to be determined,
interferometry at a single projected baselength is unlikely to
yield overall gain in accuracy in excess of a factor of two even at
optimal baselines.
 |
Figure 5:
The lower and upper limits of random error ratio (solid lines) and
distribution of optimal baseline lengths
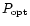 (dashed lines) for grid 5,
(dashed lines) for grid 5,
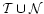 = =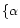 , ,
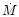 , ,
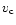 ,
T1, ,
T1, 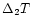 , ,
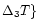 ,
and target sets comprising several parameters (indicated on the plots) ,
and target sets comprising several parameters (indicated on the plots) |
We studied further the effect of increasing the number of sublayers
MR, which permits us to investigate the influence of fine details of
the thermal
structure of the envelope. This appears to be justified because
Drew ([1985]) showed that in certain cases this structure
is quite complex, and the gradient of  varies
strongly with radial distance. Consequently, a model aiming to closely
approximate the realistic envelope should be parameterized using
a large MR (see Sect. 4.1)
and hence requires computations on grids of high dimension D.
varies
strongly with radial distance. Consequently, a model aiming to closely
approximate the realistic envelope should be parameterized using
a large MR (see Sect. 4.1)
and hence requires computations on grids of high dimension D.
Since the number of mesh points of the grid depends on D
exponentially, for computations based on such complex models (grids
5-9 from Table 1) the limited computer resources
dictate sparser mesh points along each axis of the parameter space and
a tuning of parameters controlling the computational process in such a way
as to increase the speed of computation at the expense of precision.
Although numerically less precise than computations for simpler
models, our results for more realistic grids indicate
that the conclusions derived for low
MR can be safely extrapolated for higher MR.
This point is illustrated in Fig. 6 showing the results
for single-parameter target sets for grid 7.
 |
Figure 6:
The lower and upper limits of random error ratio (solid lines) and
distribution of optimal baseline lengths
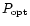 (dashed lines) for grid 7,
(dashed lines) for grid 7,
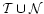 = =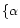 , ,
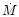 , ,
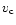 ,
T1, ,
T1, 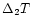 , ,
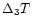 , ,
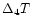 , ,
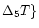 ,
and target sets consisting of a single parameter (indicated on
the plots) ,
and target sets consisting of a single parameter (indicated on
the plots) |
As can be seen in Figs. 3-6 and is confirmed
by other results not presented here, the distribution of optimal
projected baseline lengths in the majority of cases has a maximum
in the range
0.4-0.8 in dimensionless units. In some cases this maximum shifts to
higher baseline lengths, but this occurs only for a very particular choice of
 that correspond to measurements of wind temperature
gradient at distances of several stellar radii from the star with
all other model parameters considered nuisance (see e.g. bottom plots
in Figs. 4 and 6). Thus, the aforementioned
range, corresponding to 45-90 m in linear scale, can be recommended
as the optimal choice for interferometric observations aimed at
determination of global characteristics of the P Cyg wind.
that correspond to measurements of wind temperature
gradient at distances of several stellar radii from the star with
all other model parameters considered nuisance (see e.g. bottom plots
in Figs. 4 and 6). Thus, the aforementioned
range, corresponding to 45-90 m in linear scale, can be recommended
as the optimal choice for interferometric observations aimed at
determination of global characteristics of the P Cyg wind.
 |
Figure 7:
Robustness ratio for the model
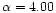 , ,
 , ,
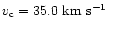 , ,
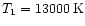 , ,
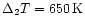 , ,
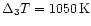 , ,
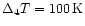 , ,
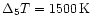 from grid 6 and
from grid 6 and
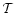 ={ ={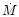 }.
Set of fixed parameters }.
Set of fixed parameters
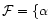 , ,
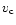 ,
T1, ,
T1,
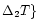 (solid line),
(solid line),
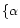 , ,
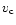 ,
T1, ,
T1, 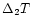 , ,
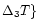 (dashed line),
(dashed line),
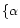 , ,
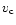 ,
T1, ,
T1, 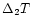 , ,
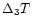 , ,
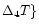 (dash-dotted line),
and
(dash-dotted line),
and
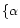 , ,
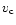 ,
T1, ,
T1, 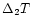 , ,
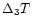 , ,
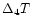 , ,
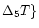 (dotted line)
(dotted line) |
The typical dependence of the robustness ratio
 on the baseline length and the set of fixed parameters for a model with
adjustable thermal structure is shown in Fig. 7. At nearly
all points of parametric space
on the baseline length and the set of fixed parameters for a model with
adjustable thermal structure is shown in Fig. 7. At nearly
all points of parametric space
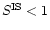 ,
and
,
and
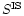 is generally lower when the set of fixed parameters
is generally lower when the set of fixed parameters
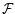 includes the values
includes the values  .
For a small fraction of
models and for short projected baselines where interferometry can not significantly
reduce random error, the value
.
For a small fraction of
models and for short projected baselines where interferometry can not significantly
reduce random error, the value
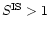 by a negligible
amount.
by a negligible
amount.
Thus, our results indicate that if the baseline length and the model
used for interpretation are chosen in such a way as to reduce random
errors, OLBI also appears able to reduce the systematic errors.


Up: Relative figure of merit
Copyright The European Southern Observatory (ESO)




