4 Models of the P Cyg wind. Computed observables

   
4.1 Stellar parameters

The star P Cyg (B1 Iape) is characterized by a high mass-loss rate and exhibits bright optical emission lines, formed in the dense and nearly fully ionized stellar wind. It belongs to the class of Luminous Blue Variables, a short-living transition phase in the evolution of a massive star at the end of the hydrogen burning (see e.g. Humphreys & Davidson [1994]; Langer et al. [1994]; Maeder [1997]).

There were at least two strong reasons to choose P Cyg as the astrophysical object of the present study. First, this bright object, $V = 4.8^{{\rm m}}$, is one of the best studied emission line stars. Although in this first trial we use simulated data, it is important to note that for P Cyg there exists a rich literature providing not only high quality spectroscopic data (e.g. Scuderi et al. [1994]), but also interferometric data (Vakili et al. [1997]), as well as thorough theoretical analysis (Drew [1985]; Pauldrach & Puls [1990]). This ensures that the present work can be followed up by a practical application. Secondly, it happens that in the growing list of outflows known to be non-spherical (e.g. Wolf et al. [1998]), P Cyg is an exception exhibiting spherical symmetry to a good degree of accuracy (Nota [1998]), becoming clumpy only on short time and small flux scales (Taylor et al. [1991]; Vakili et al. [1997]; Nota [1998]). This implies that the assumption of spherical symmetry of the envelope, used in the present work, is realistic. Note that it allows us to compute a model in a reasonable amount of time, and thus to explore a large domain of parametric space, which is a requirement for the evaluation results to be meaningful.

For the distance to the star d, its radius R_* and the effective temperature $T_{\rm eff}$ we adopted the following values: $d=1800\,{\rm pc}$, $R_*=76.0\,R_\odot$, $T_{\rm eff}=20000\,{\rm K}$ (Lamers et al. [1983]; Pauldrach & Puls [1990]). The spectrum of the star was assumed to be blackbody. Our study is limited to the hydrogen H$\alpha$ line, which is the most prominent and the best studied feature in the spectrum of the star.

   
4.2 The physical model of the envelope

The mass distribution within a spherically symmetric and stationary outflow is described by its mass loss rate $\dot M$ and the outflow velocity v, which we assume to depend on radial distance r in the following way:

$$v(r)=v_{\mathrm c}+(v_{\infty}-v_{\mathrm c})(1-1/r)^\alpha,$$

where $v_{\infty}$ is the terminal velocity of the wind, $v_{\rm c}$ is velocity of the wind at the base of the photosphere, and $\alpha$ is a dimensionless parameter that characterizes the rate at which the velocity approachs its asymptotic value at large r. The radial distance r is measured in units of stellar radius R_*, while $\dot M$, $v_{\rm c}$, $v_{\infty}$, and $\alpha$ are parameters of a model.

The temperature in the envelope is often assumed to be constant. However, as it was shown by Drew ([1985]), across the region of the H$\alpha$ line formation the temperature in the envelope can vary by as much as 6000K. Therefore, along with isothermal models, we also computed the emergent emission for non-isothermal models.

To keep a finite number of scalar parameters, the dependence of envelope temperature T(r) on radial distance is approximated in the following manner: it is assumed that T(r_i)=T_i for $r_1=1<r_2<\dots<r_{M_R}$, that T(r) is a linear function of $\log r$ at each interval [r_i,r_i+1] for 0<i<M_R-1, and that T(r)=T_MR for r>r_MR. The values r_i were fixed for each model of the family.

We consider only non-increasing temperature laws T(r), that is $\Delta_iT\geq0$ for $i=2,\dots,{M_R}$, where $\Delta_iT=T_{i-1}-T_i$. Since the computations are organized in such a way that the model parameters vary independently on each other, it is the values $\Delta_iT$ that are used along with T₁ as the parameters defining the envelope temperature, and the vector of model parameters is given by

$$\vec\Theta=(\alpha,\dot M,v_{\infty},v_{\mathrm c},T_1,\Delta_2T, \dots,\Delta_{{M_R}}T).$$

4.3 Source function and radiative transfer equation

The "supersonic'' Sobolev approximation is a well known efficient method of calculating line spectral profiles (e.g. Castor [1970]). However, it would have a low accuracy if applied in the P Cyg case, for a noticeable fraction of H$\alpha$ flux is emitted in the inner part of envelope, where the outflow velocity is comparable to that of sound. We adopted a mixed method computing the source function in the Sobolev approximation, and then finding the emergent intensities by the exact numerical solution of the transfer equation. As it was shown by Hamann ([1981]), the errors in line profiles computed in the original Sobolev approximation come mainly from calculations of the emergent intensities, whereas the source function is accurate for a wide range of physical conditions.

The choice of the model of the hydrogen atom was based on the fact that the regions of the envelope emitting the major fraction of the H$\alpha$ flux are nearly completely ionized and opaque to Lyman continuum and L$\alpha$, so that direct recombinations to and photoionizations from the ground level cancel out, and L$\alpha$ is saturated (Drew [1985]). The populations of levels n=2 and n=3 are mainly defined by collisional and radiative transitions between these two levels, radiative ionizations due to stellar radiation, and radiative recombinations (including indirect) to the level n=3. We therefore adopted the three-level + continuum model of hydrogen atom.

The balance equations for n₂ and n₃, the number densities of hydrogen atoms respectively at levels 2 and 3, take then the following form:

$$\begin{array}{rlcrlcl} n_2&(C_{23}+I_2)&-&n_3&(C_{32}+\beta_... ...&+&n_3&(C_{32}+\beta_{32} A_{32}+I_3) &=&R_3\,,\\ \end{array}$$ (20)

where A₃₂ is the spontaneous emission coefficient, C₂₃ and C₃₂ are collisional excitation and de-excitation coefficients for the transition, I₂, I₃ and R₂, R₃ are respectively ionization coefficients and recombination rates for the levels involved, and $\beta_{32}$ is the escape probability.

Since the hydrogen is nearly completely ionized, the values C₂₃, C₃₂, R₂ and R₃ can be considered independent of n₂ and n₃, the only source of non-linearity in Eqs. (20) being the terms containing $\beta_{23}$.

The escape probability $\beta_{32}$ is a rather complex function of the population of the lower level of the transition, so that commonly the Eqs. (20) are solved by iterations, which is, particularly the recalculation of the escape probability, by far the most time consuming operation.

To speed up computations, we developed a new approximate method for solving the equations of statistical equilibrium. It is based on the fact that, as shown in Appendix B, the function $\beta_{32}(n_2)$ can be approximated with sufficiently good accuracy by a simple analytic expression as follows:

$$\beta_{32}(n_2)=1/(1+n_2/n_{\mathrm{as}}),$$ (21)

where

$$n_{\mathrm{as}}= \frac{8\pi}{\lambda^3A_{32}} \frac{g_2}{g_3... ...m d}v(r)}{{\mathrm d}r} + \frac{2}{3}\frac{v(r)}{r} \right),$$ (22)

g₂ and g₃ are statistical weights of the levels, and $\lambda$is the line wavelength.

Introducing the dimensionless variables

$$P_2=n_2/n_0\,,\quad P_3=n_3/(n_0Q)\,,$$ (23)

where

$$n_0=\frac{R_2}{I_2},\quad Q=\frac{g_3}{g_2}\exp\left(-\frac{E_{23}}{kT}\right)\,,$$

and E₂₃ is the energy of transition, and substituting the approximation (21) into Eqs. (20) we obtain after some algebra that P₂ is the positive solution of the quadric equation

$$aP_2^2+bP_2+c=0\,,$$

where

$$\begin{eqnarray*}a&=&-\rho_2MS\,,\\ b&=&(\rho_2*(1-\beta_0*(\delta+S))+M*(1-\be... ...)+\rho_3)P\,,\\ c&=&\beta_0*((\rho_2+\rho_3)*(1+\delta)+M)=0\,. \end{eqnarray*}$$

Here

$$\begin{eqnarray*}\rho_i&=&R_i/(A_{32}n_0)\quad{\rm for}\quad i=2,3\,,\\ M&=&\io... ...,,\\ S&=&1+\iota Q\,,\\ \beta_0&=&1/(1+n_0/n_{\mathrm{as}})\,. \end{eqnarray*}$$

and

$$\iota=I_3/I_2\,.$$

When P₂ is calculated, the value of P₃ can be found using the relation

$$P_3=\frac{QP_2+\rho_3\delta}{Q(\iota\rho_2\delta+\beta\delta+1)}\,.$$

The source function is then easily computed from level populations, which can be obtained using Eq. (23).

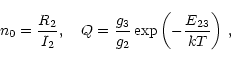
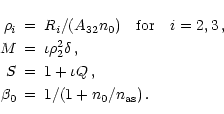
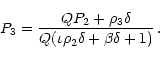
Integration of the transfer equation was performed using the code developed by Bertout ([1984]), who kindly provided it to the authors. In computing the line profile, the code assumes the envelope to be isothermal, so that its use for a non-isothermal case requires some comments. The envelope temperature enters the calculations at two points: (1) In calculating the source function, through coefficients C₂₃ and C₃₂ of Eq. (20). Since the Bertout code is applicable to arbitrary source function, variations in temperature does not cause any difficulties here. (2) In integrating the transfer equation, T(r) enters the result through the local Doppler line width. Since we consider only the envelopes with relatively low temperature contrast , and dependence of the Doppler width on temperature is rather weak, the error induced by this isothermal code structure is still negligible.

   
4.4 Computation of final results

Once the intensity $I(\vec\Theta,\lambda,p)$ is computed, the observable quantities, i.e. the emergent flux $F(\vec\Theta,\lambda)$ and the visibility squared $W(\vec\Theta,\lambda,B)$ are obtained using Eqs. (12)-(14).

The relative figure of merit $R(\vec\Theta_{\rm m}$, $\mathcal T$, $\mathcal N$,B_j) and the robustness ratio $S(\vec\Theta_{\rm m}$, $\mathcal T$, $\mathcal F$,B_j) are calculated in two stages, implemented as separate programs.

First, for the given grids of model parameters $\{\vec\Theta_{\rm m}$: $~m=1,\dots,N_{\rm m}\}$ and the projected baseline lengths $\{B_j$: $~j=1,\dots,N_B\}$, we calculate and store the matrices $\left(\tens C^{\rm S}\right) ^{-1}$ and $\left(\tens C^{\rm I}\right) ^{-1}$, defined in Eqs. (11) and (18). The defining parameters of the grids are entered as input data, the grid of models being constructed as the direct product of uniform grids for individual parameters.

The derivatives entering definitions of the matrices are approximated by finite differences. All the model parameters that are not constant on the grid are treated as adjustable, that is either target or nuisance. The distinction between those two types of parameters is irrelevant at this stage.

At the second stage, for given partitions of set $\mathcal T\cup\mathcal N$of all adjustable parameters on the subsets $\mathcal T$ and $\mathcal N$, we compute the values of $R(\vec\Theta_{\rm m}$, $\mathcal T$, $\mathcal N$,B_j) and $S(\vec\Theta_{\rm m}$, $\mathcal T$, $\mathcal F$,B_j) (see Eqs. (3) and (5)) on the grid. In this way, the dependence of the results on $\mathcal T$ and $\mathcal N$ can be studied without repeating the time consuming physical modeling of the envelope.