

Up: Relative figure of merit
Subsections
In this section we obtain the expressions for the elements of the
covariance matrix
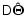 in the form that can be
directly used to compare the OLBI and spectroscopy.
in the form that can be
directly used to compare the OLBI and spectroscopy.
First, the measurement errors have to be specified. For this first
trial application, the only considered source of random errors is the
photon noise. Other sources of error, in particular those in OLBI
arising from atmospheric seeing and calibrations of the modulation
transfer function (see Roddier & Léna [1984]; Mourard et
al. [1994]) are important and have to be incorporated in
future work.
Also, the spectral coverage and the spectral resolution have to be
specified. We assume that they are the same for both kinds of
observations; the covered spectral region is
![$[\lambda_1,\lambda_2]$](/articles/aas/full/2000/05/ds8950/img106.gif) ,
the spectral resolution is sufficiently high, i.e. the monochromatic
intensity received from each point of the observed object remains
nearly constant across each spectral channel.
In other words, we assume that
,
the spectral resolution is sufficiently high, i.e. the monochromatic
intensity received from each point of the observed object remains
nearly constant across each spectral channel.
In other words, we assume that
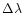 ,
the width of the spectral channels, in
terms of velocity is lesser than the thermal velocity of the emitting
atoms. For the P Cyg type envelopes this corresponds to
,
the width of the spectral channels, in
terms of velocity is lesser than the thermal velocity of the emitting
atoms. For the P Cyg type envelopes this corresponds to
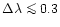 Å, which is easily satisfied with modern
spectrographs. Then one can formally consider the convenient limit
case
Å, which is easily satisfied with modern
spectrographs. Then one can formally consider the convenient limit
case
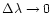 .
In this case, the resulting covariance
matrices tend to a limit which is independent of the spectral
resolution (cf. Eqs. (11) and (18)).
.
In this case, the resulting covariance
matrices tend to a limit which is independent of the spectral
resolution (cf. Eqs. (11) and (18)).
3.1 Spectroscopy
The physical quantity provided by spectroscopy is the flux density as
a function of wavelength. In terms of observables, it is given by the
vector
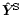 with the components
with the components
 |
(6) |
where 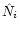 is the number of photons recorded in the
i-th spectral channel during the exposure, and L is the number
of channels. The random values
is the number of photons recorded in the
i-th spectral channel during the exposure, and L is the number
of channels. The random values 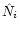 are related to the
physical parameters of the object by
are related to the
physical parameters of the object by
 |
(7) |
where
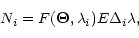 |
(8) |
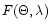 is the monochromatic flux from the object at
wavelength
is the monochromatic flux from the object at
wavelength 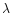 ,
,
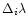 is the width of i-th
spectral channel, and ni is the measurement error due to the photon
noise, with the variance given by
is the width of i-th
spectral channel, and ni is the measurement error due to the photon
noise, with the variance given by
 |
(9) |
Finally the factor E is given by
where
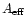 is the instrument effective aperture and
t is the exposure time.
Hereafter we suppose that
is the instrument effective aperture and
t is the exposure time.
Hereafter we suppose that
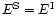 ,
where
,
where  and
and 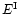 pertain to the spectrometer and the interferometer respectively.
Since the values
pertain to the spectrometer and the interferometer respectively.
Since the values  and
and 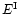 enter
the final results only through the ratio
enter
the final results only through the ratio
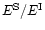 ,
we can for the sake of simplicity set
,
we can for the sake of simplicity set
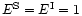 .
.
Thus,
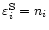 and the elements of the covariance matrix of measurement errors are
given by
and the elements of the covariance matrix of measurement errors are
given by
 |
(10) |
Substituting Eqs. (6)-(10) into
Eq. (1)
and proceeding to the limit
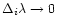 we obtain:
we obtain:
 |
(11) |
For spherically symmetric objects considered in the present paper,
 |
(12) |
where
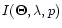 is the monochromatic intensity at the
angular distance p from the center of the object.
is the monochromatic intensity at the
angular distance p from the center of the object.
3.2 OLBI
We consider the case of a two-aperture OLBI with an adjustable baseline. The physical
quantity eventually provided by OLBI measurements is the fringe
visibility V as a function of the baseline vector. The visibility V is equal
to the real part of the complex degree of coherence, and therefore is
the Fourier transform of the brightness distribution in the focal
plane by virtue of the Van Cittert - Zernicke theorem (e.g. Mariotti
[1998], textbooks of Perina [1972], and Goodman
[1985]). However, the value estimated in practice is
V2. We refer the reader for details to the thorough discussion
by Mourard et al. ([1994]). In the present analysis we
consider the estimates  of the quantity
of the quantity
 |
(13) |
where i refers (as previously) to the i-th spectral channel, and B
is the projected baseline length of the interferometer.
In the case of spherically symmetric objects
the intensity distribution is circularly symmetric and
V is given by the
normalized Hankel transform as follows (e.g. Bracewell [1978]):
 |
(14) |
where J0 is the Bessel function, and
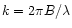 .
.
Statistical errors
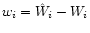 obey the equations
obey the equations
 |
(15) |
and
 |
(16) |
The validity of Eqs. (15) and (16) for 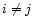 is evident. The case i=j is treated in Appendix A.
is evident. The case i=j is treated in Appendix A.
As a rule, the spectrum of the object, i.e. the values 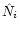 ,
is
also recorded. Consequently, the vector of observables for the OLBI
and the elements of its covariance matrix of errors are given by
,
is
also recorded. Consequently, the vector of observables for the OLBI
and the elements of its covariance matrix of errors are given by
 |
(17) |
and
Substituting these expressions into Eq. (1),
we obtain in the limit
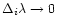 that
that
 |
(18) |
where
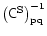 is
defined in Eq. (11).
is
defined in Eq. (11).
3.3 The relative figure of merit
As discussed in Sect. 2.2, the relative figure of merit of
OLBI as compared to spectroscopy is the random error ratio:
 |
(19) |
From Eqs. (18) and (19), it follows that
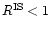 ,
which merely reflects the fact that the
observables of spectroscopy constitute a subset of the OLBI
observables. Consequently, in the adopted comparison, the statistical
errors in parameter determination by OLBI are always less than those
obtained when only spectroscopic data are used, if however the
spectroscopic data are of equal precision.
,
which merely reflects the fact that the
observables of spectroscopy constitute a subset of the OLBI
observables. Consequently, in the adopted comparison, the statistical
errors in parameter determination by OLBI are always less than those
obtained when only spectroscopic data are used, if however the
spectroscopic data are of equal precision.
As explained in Sect. 3.1, the Eq. (19)
is obtained in the assumption that
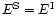 .
To compare a pair of instruments
for which that equality does not hold, the RHS of
Eq. (19) should be multiplied by
.
To compare a pair of instruments
for which that equality does not hold, the RHS of
Eq. (19) should be multiplied by
 .
.


Up: Relative figure of merit
Copyright The European Southern Observatory (ESO)
![]() ,
the spectral resolution is sufficiently high, i.e. the monochromatic
intensity received from each point of the observed object remains
nearly constant across each spectral channel.
In other words, we assume that
,
the spectral resolution is sufficiently high, i.e. the monochromatic
intensity received from each point of the observed object remains
nearly constant across each spectral channel.
In other words, we assume that
![]() ,
the width of the spectral channels, in
terms of velocity is lesser than the thermal velocity of the emitting
atoms. For the P Cyg type envelopes this corresponds to
,
the width of the spectral channels, in
terms of velocity is lesser than the thermal velocity of the emitting
atoms. For the P Cyg type envelopes this corresponds to
![]() Å, which is easily satisfied with modern
spectrographs. Then one can formally consider the convenient limit
case
Å, which is easily satisfied with modern
spectrographs. Then one can formally consider the convenient limit
case
![]() .
In this case, the resulting covariance
matrices tend to a limit which is independent of the spectral
resolution (cf. Eqs. (11) and (18)).
.
In this case, the resulting covariance
matrices tend to a limit which is independent of the spectral
resolution (cf. Eqs. (11) and (18)).
![]() and the elements of the covariance matrix of measurement errors are
given by
and the elements of the covariance matrix of measurement errors are
given by
![]() obey the equations
obey the equations
![]() ,
is
also recorded. Consequently, the vector of observables for the OLBI
and the elements of its covariance matrix of errors are given by
,
is
also recorded. Consequently, the vector of observables for the OLBI
and the elements of its covariance matrix of errors are given by
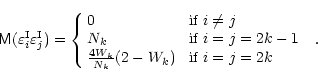
![]() .
To compare a pair of instruments
for which that equality does not hold, the RHS of
Eq. (19) should be multiplied by
.
To compare a pair of instruments
for which that equality does not hold, the RHS of
Eq. (19) should be multiplied by
![]() .
.