2 Relative figure of merit of observational methods

   
2.1 Definitions and general theory

We consider astrophysical observations and their interpretation in the framework of the theory of parameter estimation (e.g. Kendall & Stuart [1967]). That is, the observed object is assumed to be exactly described by a fixed multiparametric physical model, the errors being solely those of the experimental measurements (see however Sect. 2.3). Any observable quantity is then a function of the vector of $M_{\rm P}$ model parameters $\vec \Theta=(\Theta_1,\Theta_2,\ldots,\Theta_{M_{\rm P}})$.

An observation consists of finding the values of $M_{\rm O}$ observables $\vec{\hat Y}=(\hat Y_1,\hat Y_2,\ldots,\hat Y_{M_{\rm O}})$, where each observable $\hat Y_i$ is either measured directly or can be calculated in a model-independent way as a known function of directly measurable quantities. Obviously, observations with instruments of different types provide observables of different numbers and natures.

The i-th observable can be represented as $\hat Y_i=Y_i(\vec\Theta)+\varepsilon_i$, where $Y_i(\vec\Theta)$ is the "theoretical'' value of the corresponding observable in the absence of observational errors and $\vec\varepsilon =(\varepsilon_1,\varepsilon_2,\ldots,\varepsilon_{M_{\rm O}})$ is the random vector of observational errors, which is assumed here to be distributed normally. We consider the case when $M_{\rm O}>M_{\rm P}$ and the parameters $\vec\Theta$ could have been uniquely determined if the vector $\vec Y$ were known.

We shall call the parameters to be determined the "target parameters'' and denote a set of $M_{\rm T}$ target parameters, or target set, as $\mathcal T$. It is possible that $M_{\rm T}<M_{\rm P}$ and the set $\mathcal T$ is a proper subset of the set of all parameters of the model. A situation of this kind may arise for two reasons. First, a model parameter may be set to some a priori fixed value because, say, it has been measured earlier by entirely different methods. This reduces the dimension of the problem and computational difficulties, the general method remaining the same. Let $\mathcal {\rm F}$ denote the set of $M_{\rm F}$ fixed parameters, and $\tilde\Theta_{\rm f}$ be the value a priori assigned to a parameter $\Theta_{\rm f}\in\mathcal F$.

Secondly, some of the unknown physical parameters may eventually be considered "not interesting'' if their values are not relevant to the astrophysical problem under study. Following the theory of parameter estimation, we will call them the "nuisance'' parameters and denote the set of nuisance parameters, or "nuisance set'', as $\mathcal N$, their number being $M_{\rm N}$. As a rule, their influence can be separated in the error analysis only at the final stage of computations, for their values are to be calculated along with the values of target parameters.

Interpretation of an observation consists of calculating the vector ${\vec{\hat \Theta}}_{\rm T}(\vec{\hat Y}) = (\hat \Theta_{t(1)},\hat \Theta_{t(2)},\ldots, \hat \Theta_{t(M_{\rm T})})$that provides the best fit to the observed values Y. Here t(i) is the index of the component of vector $\Theta$corresponding to the same model parameter as the i-th target parameter ( $i=1,\ldots,M_{\rm T}$).

The precision of the values $\vec{\hat \Theta}_{\rm T}$ resulting from interpretation of the observations is characterized by ${\tens M}(\vec{\hat \Theta}_{\rm T}-\vec\Theta_{\rm T})$and ${\tens D}\vec{\hat \Theta}_{\rm T}$, where for any random vector $\vec\xi$ expressions ${\tens M}\vec\xi$ and ${\tens D}\vec\xi$ denote its mean and its covariance matrix respectively, and $\vec\Theta_{\rm T}= (\Theta_{t(1)}, \Theta_{t(2)},\ldots, \Theta_{t(M_{\rm T})})$.

In what follows, we assume that $\vec{\hat Y}$ is an unbiased estimate of $\vec Y$, i.e. ${\tens M}{\vec\varepsilon}=0$, and that the measurement errors are small enough, so that the error analysis can be performed using the linearized version of the least squares method.

We additionally assume that all a priori fixed parameters are set to their true values (see however Sect. 2.3), that is $\tilde\Theta_{\rm f}=\Theta_{\rm f}$ for any $\Theta_{\rm f}\in\mathcal F$, then ${\tens M}{\vec{\hat \Theta}=\vec\Theta}$and statistical properties of errors in parameter determination are completely characterized by the covariance matrix of errors $\tens C = {\tens D}\vec{\hat \Theta}$.

  
2.2 Random errors and the relative figure of merit

According to Kendall & Stuart ([1967, Chap. 19]), the covariance matrix of errors C is related to $\vec Y$ and $\vec\Theta$ by the following expression:

$$\tens C(\vec\Theta,\mathcal T,\mathcal N) =\left({\tens A}^{... ...{\tens D}\vec\varepsilon\/\right)}^{-1} \tens A \right)^{-1}$$ (1)

where $\tens A$ is the $M_{\rm O}\times (M_{\rm T}+M_{\rm N})$ matrix with elements $A_{ij} = \frac {\partial Y_i} {\partial \Theta_j}$for $\Theta_j\in\mathcal T\cup\mathcal N$ and $\vec\varepsilon$ is the vector of experimental errors defined in Sect. 2.1.

The natural scalar characteristics of the precision of parameter determination for a given set $\mathcal T$ of target parameters is the following principal subdeterminant of the covariance matrix:

 

$${C(\vec\Theta,\mathcal T,\mathcal N)=}$$

$$\det \left\vert \begin{array}{llcl} \tens C_{t(1)t(1)}&\tens C_{t... ...&\ldots& \tens C_{t(M_{\mathrm T})t(M_{\mathrm T})} \end{array}\right\vert\cdot$$ =

Geometrically, this subdeterminant is proportional to the hypervolume of the scattering ellipsoid in the space of target parameters. It depends not only on the physical model and errors of measurements, but also on the analytical form used for description of the model: two physically equivalent but mathematically different (e.g. interrelated by a reversible substitution of variables) analytical representations could yield entirely different values of $C(\vec\Theta,\mathcal T,\mathcal N)$.

However, a pair of observational methods can well be compared if one makes use of the ratio

$$R(\vec\Theta,\mathcal T,\mathcal N)= \left( C^{{\rm I}}(\v... ...(\vec\Theta,\mathcal T,\mathcal N) \right)^{1/M_{\mathrm T}},$$ (3)

where $C^{{\rm I}}$ and $C^{{\rm II}}$ are the subdeterminants calculated for the observation of the same object with instruments I and II. This ratio depends only on the physical model used, and the achieved precision on the definition of the model parameters. We shall call the quantity $R(\vec\Theta,\mathcal T,\mathcal N)$, introduced by the Eq. (3), the "random error ratio'', or the "relative figure of merit''.

If the instruments are of the same kind, and differ from each other only in precision, the value $R(\vec\Theta,\mathcal T,\mathcal N)$ is merely the ratio of observational errors. If the instruments are different, providing observables of different nature and number, and the target set consists of only one model parameter, the value $R(\vec\Theta,\mathcal T,\mathcal N)$ is merely the ratio of resulting random errors in the parameter determination. However, in the general case of instruments of arbitrary kinds and multiparametric models, no simple ratio of errors exists, and the evaluation of relative merits can be done only using the quantity $R(\vec\Theta,\mathcal T,\mathcal N)$ defined by Eq. (3).

This allows us to compare various observational techniques applied to objects described by various multiparametric models: equality $R(\vec\Theta,\mathcal T,\mathcal N)<1$ means that instrument I is better suited for determination of parameters from the target set than instrument II.

  
2.3 Systematic errors induced by interpretation

The fact that the description of an object by a multiparametric physical model is only an approximation to reality implies that we have to consider the robustness of the method, that is the stability of the results it yields with respect to deviations of the real situation from the model.

The present framework offers a way to obtain certain quantitative characteristics of the robustness. Indeed, let us consider a multiparametric model with $\mathcal F\neq\emptyset$. If $\tilde\Theta_{\rm f}\neq\Theta_{\rm f}$ for some $\Theta_{\rm f}\in\mathcal F$ then, in general, ${\tens M}{\hat\Theta_{\rm t}}-\Theta_{\rm t} \neq 0$ for $\Theta_{\rm t}\in\mathcal T$. That is, in addition to random errors of observational origin, the result is biased by systematic errors due to inaccurate interpretation. The value of that bias characterizes the robustness of the method with respect to deviations of $\tilde\Theta_{\rm f}$ from its true value.

In the linear approximation, ${\tens M}(\hat\Theta_{\rm t}-\Theta_{\rm t}) =\tens S\times(\tilde\Theta_{\rm f}-\Theta_{\rm f})$, where $\tens S$ is the $M_{\rm T}\times M_{\rm F}$ matrix with elements

$$% \tens S_{{\rm tf}}= \frac {\partial \Theta_{\rm t}} {\partial \Theta_{\rm f}}\,,$$

where $\Theta_{\rm t}\in\mathcal T,\quad\Theta_{\rm f}\in\mathcal F$.

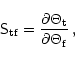
A comprehensive study of systematic errors requires a joint analysis of individual elements of the matrix $\tens S$ and uncertainties in model parameters from $\mathcal F$. In the present paper, we will develop a simplified approach providing semiquantitative indications concerning the relative robustness of different observational techniques.

Let us first define for each observational method under consideration the value

$$U(\Theta,\mathcal T,\mathcal F) =(C(\Theta,\mathcal T,\mathcal F)/C(\Theta,\mathcal T,\emptyset))^{1/M_{\mathrm T}}\,.$$ (4)

When the estimates for target parameters are uncorrelated with estimates for parameters from $\mathcal F$, equality U=1 takes place: the method is robust (with respect to deviations of specified form from the model). When such a correlation exists, U exceeds unity; the closer the correlation, the larger its value, eventually implying poor robustness of the method.

Further, to compare the robustness of methods I and II with respect to inaccuracies in parameters from $\mathcal F$, we will define the "robustness ratio S'' as follows:

$$S(\vec\Theta,\mathcal T,\mathcal F) =U^{{\rm I}}/U^{{\rm II... ...heta,\mathcal T,\mathcal F)/R(\vec\Theta,\mathcal T,\emptyset)$$ (5)

where function R is defined in Eq. (3). Note that once the values of $R(\Theta,\mathcal T,\mathcal N)$, which are necessary for analysis of random errors, are found, comparison of robustness is straightforward.