In Table 1, we present the energies resulting from these CI calculations in
comparison to available experimental data. The LS designations should be
considered as labels only; for many of these levels, there is strong mixing
due to the electrostatic interactions between LS terms with different parents,
the spin-orbit interactions, and the interactions between configurations.
For example, level 50 labeled as 3p53d2(3F)2D3/2 in
Table 1 is actually:
0.845 ![]() 3p53d2(3F)2D3/2 +
0.418
3p53d2(3F)2D3/2 +
0.418 ![]() 3p53d2(1D)2D3/2 +
0.329
3p53d2(1D)2D3/2 +
0.329 ![]() 3p53d2(3P)2D3/2plus some smaller eigenvector components; this amount of mixing between
different LS parents is typical of many of the levels of the 3p53d2configuration.
3p53d2(3P)2D3/2plus some smaller eigenvector components; this amount of mixing between
different LS parents is typical of many of the levels of the 3p53d2configuration.
We see that the agreement between experiment and theory is quite good for those
few lower levels of the 3p53d2 configuration for which experimental
measurements exist; however, the differences grow to an average of 3.2 eV for
the 6 highest levels of this configuration, all of which are important
because of their strong radiative rates to the ground-state configuration.
On the other hand, the average differences between experiment and theory for the
levels of 3p64p, 3p64f, and 3p53d4s are only 1.11 eV, 1.64 eV, and 1.49 eV,
respectively. In order to account for ground-state correlation, it would have
been necessary to include such configurations as 3s03p63d3,
3s3p63d2, and 3s23p43d3 in our configuration-interaction expansion
of the target; but then, in order to account for final-state correlation, one
should also include the configurations formed from single and double promotions
from the 3s subshell to the 3d subshell and double promotions from the 3p
subshell to the 3d subshell for all excited configurations, and that would
have made the problem prohibitively large. Finally, if the levels of
3s23p65![]() and 3s3p63d2 (which are in the same energy range as
some of the upper levels in our present calculation) had been included in our
close-coupling expansion of the target, they would have some effect
on our scattering calculations to the more highly excited states through both
coupling, which would have tended to decrease the cross sections, and resonance
contributions, which would have enhanced the cross sections. However, to
include these configurations in our close-coupling expansion would have added
10 LS terms and 25 levels to an already large calculation.
and 3s3p63d2 (which are in the same energy range as
some of the upper levels in our present calculation) had been included in our
close-coupling expansion of the target, they would have some effect
on our scattering calculations to the more highly excited states through both
coupling, which would have tended to decrease the cross sections, and resonance
contributions, which would have enhanced the cross sections. However, to
include these configurations in our close-coupling expansion would have added
10 LS terms and 25 levels to an already large calculation.
| Index | Level | Theor. | Exp. | Index | Level | Theor. | Exp. | |
| Energy | Energy a | Energy | Energy a | |||||
| 1 | 3p63d 2D3/2 | 0.00 | 0.00 | 2 | 3p63d 2D5/2 | 0.24 | 0.23 | |
| 3 | 3p53d2(3F)4D1/2 | 47.75 | --- | 4 | 3p53d2(3F)4D3/2 | 47.86 | --- | |
| 5 | 3p53d2(3F)4D5/2 | 48.05 | --- | 6 | 3p53d2(3F)4D7/2 | 48.34 | --- | |
| 7 | 3p53d2(3F)4G11/2 | 50.62 | --- | 8 | 3p53d2(3F)4G9/2 | 50.82 | --- | |
| 9 | 3p53d2(3F)4G7/2 | 51.07 | --- | 10 | 3p53d2(3P)4P5/2 | 51.20 | --- | |
| 11 | 3p53d2(3F)4G5/2 | 51.34 | --- | 12 | 3p53d2(3P)4P3/2 | 51.57 | --- | |
| 13 | 3p53d2(3P)4P1/2 | 51.85 | --- | 14 | 3p53d2(3F)4F3/2 | 52.57 | --- | |
| 15 | 3p53d2(3F)4F5/2 | 52.73 | --- | 16 | 3p53d2(3F)4F9/2 | 52.80 | --- | |
| 17 | 3p53d2(3F)4F7/2 | 52.91 | --- | 18 | 3p53d2(1D)2D5/2 | 53.34 | --- | |
| 19 | 3p53d2(1G)2F5/2 | 53.43 | 53.47 | 20 | 3p53d2(1D)2D3/2 | 53.56 | --- | |
| 21 | 3p64s 2S1/2 | 53.75 | --- | 22 | 3p53d2(1G)2F7/2 | 53.88 | 53.88 | |
| 23 | 3p53d2(1D)2P1/2 | 54.60 | --- | 24 | 3p53d2(1D)2P3/2 | 55.27 | --- | |
| 25 | 3p53d2(1G)2H11/2 | 55.35 | --- | 26 | 3p53d2(1D)2F7/2 | 55.62 | 55.50 | |
| 27 | 3p53d2(3F)2G7/2 | 55.95 | --- | 28 | 3p53d2(3F)2G9/2 | 56.30 | --- | |
| 29 | 3p53d2(1G)2H9/2 | 56.60 | --- | 30 | 3p53d2(1D)2F5/2 | 57.09 | 56.95 | |
| 31 | 3p53d2(3P)4D7/2 | 57.24 | --- | 32 | 3p53d2(3P)4D5/2 | 57.41 | --- | |
| 33 | 3p53d2(3P)4D3/2 | 57.65 | --- | 34 | 3p53d2(3P)4D1/2 | 57.88 | --- | |
| 35 | 3p53d2(3P)2D3/2 | 59.99 | --- | 36 | 3p53d2(3P)2D5/2 | 60.48 | --- | |
| 37 | 3p53d2(3P)4S3/2 | 60.80 | --- | 38 | 3p53d2(3P)2S1/2 | 60.80 | --- | |
| 39 | 3p53d2(1G)2G9/2 | 61.19 | --- | 40 | 3p53d2(1G)2G7/2 | 61.28 | --- | |
| 41 | 3p53d2(1S)2P3/2 | 64.14 | 63.05 | 42 | 3p64p 2P1/2 | 64.28 | 63.27 | |
| 43 | 3p64p 2P3/2 | 65.02 | 63.92 | 44 | 3p53d2(1S)2P1/2 | 65.69 | 64.57 | |
| 45 | 3p53d2(3F)2F5/2 | 69.17 | 66.44 | 46 | 3p53d2(3F)2F7/2 | 69.86 | 67.17 | |
| 47 | 3p53d2(3P)2P1/2 | 76.33 | 73.39 | 48 | 3p53d2(3P)2P3/2 | 76.70 | 73.79 | |
| 49 | 3p53d2(3F)2D5/2 | 77.86 | 73.95 | 50 | 3p53d2(3F)2D3/2 | 77.88 | 74.03 | |
| 51 | 3p64d 2D3/2 | 82.72 | --- | 52 | 3p64d 2D5/2 | 82.77 | --- | |
| 53 | 3p64f 2F5/2 | 96.33 | 94.69 | 54 | 3p64f 2F7/2 | 96.34 | 94.70 | |
| 55 | 3p53d(3P)4s 4P1/2 | 103.49 | --- | 56 | 3p53d(3P)4s 4P3/2 | 103.79 | --- | |
| 57 | 3p53d(3P)4s 4P5/2 | 104.35 | --- | 58 | 3p53d(3P)4s 2P1/2 | 105.14 | 103.86 | |
| 59 | 3p53d(3P)4s 2P3/2 | 105.78 | 104.50 | 60 | 3p53d(3F)4s 4F9/2 | 105.84 | --- | |
| 61 | 3p53d(3F)4s 4F7/2 | 106.15 | 105.03 | 62 | 3p53d(3F)4s 4F5/2 | 106.48 | 105.37 | |
| 63 | 3p53d(3F)4s 4F3/2 | 106.81 | 105.74 | 64 | 3p53d(3F)4s 2F7/2 | 107.36 | 106.00 | |
| 65 | 3p53d(3F)4s 2F5/2 | 108.03 | 106.70 | 66 | 3p53d(3D)4s 4D7/2 | 110.02 | 108.45 | |
| 67 | 3p53d(3D)4s 4D5/2 | 110.26 | 108.70 | 68 | 3p53d(3D)4s 4D3/2 | 110.38 | 108.79 | |
| 69 | 3p53d(3D)4s 4D1/2 | 110.47 | 108.89 | 70 | 3p53d(1D)4s 2D5/2 | 110.75 | 108.98 | |
| 71 | 3p53d(1D)4s 2D3/2 | 110.99 | 109.27 | 72 | 3p53d(1F)4s 2F5/2 | 111.22 | 109.64 | |
| 73 | 3p53d(1F)4s 2F7/2 | 111.49 | 110.01 | 74 | 3p53d(3D)4s 2D3/2 | 111.94 | 110.24 | |
| 75 | 3p53d(3D)4s 2D5/2 | 112.07 | 110.45 | 76 | 3p53d(1P)4s 2P3/2 | 129.51 | --- | |
| 77 | 3p53d(1P)4s 2P1/2 | 129.51 | --- |
In Table 2, we compare the radiative rates that result from the two
CI calculations for these particular transitions. For both calculations, we
adjusted the energies to the experimental values before calculating the
rates. As can be seen, this extra CI reduces the radiative rates for the
transitions from the 6 highest levels of the 3p53d2 configuration by an
average of 21%. On the other hand, the radiative rates for the transitions
from the 3p64f configuration are reduced by less than 10%.
| Transition | Ratio c | ||
| 3p53d2(3F)2F
|
1.32 1011 | 0.98 1011 | 0.742 |
| 3p53d2(3F)2F
|
6.68 109 | 4.49 109 | 0.672 |
| 3p53d2(3F)2F
|
1.42 1011 | 1.04 1011 | 0.732 |
| 3p53d2(3P)2P
|
2.79 1011 | 2.27 1011 | 0.814 |
| 3p53d2(3P)2P
|
2.81 1010 | 2.50 1010 | 0.890 |
| 3p53d2(3P)2P
|
2.53 1011 | 2.05 1011 | 0.810 |
| 3p53d2(3F)2D
|
2.25 1010 | 1.67 1010 | 0.742 |
| 3p53d2(3F)2D
|
3.59 1011 | 3.05 1011 | 0.850 |
| 3p53d2(3F)2D
|
3.48 1011 | 2.93 1011 | 0.842 |
| 3p53d2(3F)2D
|
3.78 1010 | 3.12 1010 | 0.825 |
| 3p64f 2F
|
1.81 1011 | 1.64 1011 | 0.906 |
| 3p64f 2F
|
1.32 1010 | 1.19 1010 | 0.902 |
| 3p64f 2F
|
1.96 1011 | 1.78 1011 | 0.908 |
In the present case, we first performed an LS R-matrix calculation with
exchange, which included all 33 terms arising from the 3p63d, 3p53d2,
3p53d4s, 3p64s, 3p64p, 3p64d, and 3p64f configurations in the
close-coupling expansion and all LS![]() partial waves from L = 0 to 14. This
allowed us to use our ICFT transformation method to generate the contributions
between the 77 levels listed in Table 1 for the J
partial waves from L = 0 to 14. This
allowed us to use our ICFT transformation method to generate the contributions
between the 77 levels listed in Table 1 for the J![]() partial waves
from J = 0 to 12. However, this partial-wave expansion must be extended to
much higher values of J in order to provide accurate data for
collisional-radiative modeling calculations. Therefore, we also performed a
no-exchange LS R-matrix calculation for all LS
partial waves
from J = 0 to 12. However, this partial-wave expansion must be extended to
much higher values of J in order to provide accurate data for
collisional-radiative modeling calculations. Therefore, we also performed a
no-exchange LS R-matrix calculation for all LS![]() partial waves from
L = 11 to 50; this allowed us to generate intermediate-coupling results for
all J
partial waves from
L = 11 to 50; this allowed us to generate intermediate-coupling results for
all J![]() partial waves from J = 13 to 48. These high J contributions were
then topped-up for the dipole-allowed transitions using a method originally
described by Burgess [1974] for LS coupling and implemented in our
ICFT program for intermediate coupling; additionally, the non-dipole transitions
were topped-up assuming a geometric series in J.
partial waves from J = 13 to 48. These high J contributions were
then topped-up for the dipole-allowed transitions using a method originally
described by Burgess [1974] for LS coupling and implemented in our
ICFT program for intermediate coupling; additionally, the non-dipole transitions
were topped-up assuming a geometric series in J.
For all our calculations, the size of the R-matrix box was set to 8.02 a.u., 27 basis orbitals were used to represent the continuum orbitals for each value of the angular momentum; this was more than sufficient to allow us to carry out our calculations to a maximum energy of 600 eV. The long-range multipole contributions were included in the asymptotic region. For the asymptotic part of the calculation, we found that an energy mesh with a separation between adjacent energy points of 0.0165 eV allowed us to resolve the vast majority of narrow resonances in the energy range up through the highest threshold.
In Figs. 1, 2, 3, and 4, we show our
calculated cross section from the two levels of 3p63d to the highest
six levels of the 3p53d2 configuration and to the two levels of the
3p64f configuration. As can be seen, the non-dipole allowed transitions
3p63d 2D3/2
![]() 3p53d2(3F)2F7/2 and
3p63d 2D5/2
3p53d2(3F)2F7/2 and
3p63d 2D5/2
![]() 3p53d2(3P)2P1/2 are
dominated by resonance contributions in the low-energy region. In addition,
resonant contributions are important in the low-energy region for the
dipole-allowed transitions
3p63d 2D3/2
3p53d2(3P)2P1/2 are
dominated by resonance contributions in the low-energy region. In addition,
resonant contributions are important in the low-energy region for the
dipole-allowed transitions
3p63d 2D3/2
![]() 3p53d2(3F)2F5/2,
3p63d 2D5/2
3p53d2(3F)2F5/2,
3p63d 2D5/2
![]() 3p53d2(3F)2F5/2, and
3p63d 2D5/2
3p53d2(3F)2F5/2, and
3p63d 2D5/2
![]() 3p53d2(3F)2F7/2,
but are of less importance for the other transitions shown.
3p53d2(3F)2F7/2,
but are of less importance for the other transitions shown.
 |
Figure 1: Electron-impact excitation cross sections for transitions from the levels of 3p63d 2D to the levels of 3p53d2(3F)2F in Fe7+ |
 |
Figure 2: Electron-impact excitation cross sections for transitions from the levels of 3p63d 2D to the levels of 3p53d2(3P)2P in Fe7+ |
 |
Figure 3: Electron-impact excitation cross sections for transitions from the levels of 3p63d 2D to the levels of 3p53d2(3F)2D in Fe7+ |
 |
Figure 4: Electron-impact excitation cross sections for transitions from the levels of 3p63d 2D to the levels of 3p64f 2F in Fe7+ |
For collisional-radiative modeling calculations, we require rate coefficients,
rather than cross sections. However, the effective collision strength, first
introduced by Seaton (Seaton [1953]), is much more convenient for input
to such calculations because it has a much more gradual variation with the
electron temperature than the rate coefficient. It is defined by the equation:
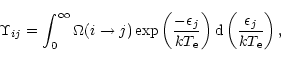 |
(1) |
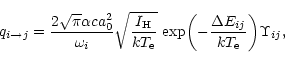 |
(2) |
 |
(3) |
Our table of collision strengths for the 2926 transitions among the 77 LSJ
levels listed in Table 1 is far too large to be shown here. However,
in Table 3, we show the effective collision strengths for the
same transitions for which we presented cross sections in Figs. 1,
2, 3, and 4. It is the transitions to the four
highest levels of the 3p53d2 configuration and the two levels of the
3p64f configuration that are of primary importance for the line-emission
intensity ratios discussed in the next section.
| Electron temperature (K) | ||||||
| Transition | 6.40 104 | 1.28 105 | 3.20 105 | 6.40 105 | 1.28 106 | 3.20 106 |
| 3p63d 2D3/2
|
4.44 | 4.47 | 4.62 | 4.99 | 5.72 | 7.24 |
| 3p63d 2D3/2
|
0.268 | 0.215 | 0.143 | 0.100 | 0.069 | 0.042 |
| 3p63d 2D3/2
|
2.04 | 2.08 | 2.18 | 2.39 | 2.77 | 3.55 |
| 3p63d 2D3/2
|
0.454 | 0.451 | 0.462 | 0.498 | 0.571 | 0.721 |
| 3p63d 2D3/2
|
0.464 | 0.475 | 0.500 | 0.546 | 0.634 | 0.810 |
| 3p63d 2D3/2
|
4.59 | 4.71 | 4.98 | 5.49 | 6.41 | 8.26 |
| 3p63d 2D3/2
|
0.878 | 0.892 | 0.954 | 1.10 | 1.35 | 1.89 |
| 3p63d 2D3/2
|
0.128 | 0.118 | 0.097 | 0.087 | 0.066 | 0.051 |
| 3p63d 2D5/2
|
0.567 | 0.488 | 0.404 | 0.371 | 0.374 | 0.422 |
| 3p63d 2D5/2
|
6.35 | 6.36 | 6.55 | 7.05 | 8.06 | 10.2 |
| 3p63d 2D5/2
|
0.055 | 0.039 | 0.026 | 0.021 | 0.017 | 0.014 |
| 3p63d 2D5/2
|
3.71 | 3.78 | 3.97 | 4.34 | 5.03 | 6.42 |
| 3p63d 2D5/2
|
7.19 | 7.39 | 7.82 | 8.61 | 10.1 | 13.0 |
| 3p63d 2D5/2
|
0.525 | 0.538 | 0.565 | 0.619 | 0.718 | 0.918 |
| 3p63d 2D5/2
|
0.202 | 0.193 | 0.175 | 0.168 | 0.171 | 0.194 |
| 3p63d 2D5/2
|
1.34 | 1.36 | 1.44 | 1.64 | 2.01 | 2.78 |
Copyright The European Southern Observatory (ESO)