Consider first the synchronized solutions,
![]() ,
,
![]() ,
for positions and velocities, respectively, at the cycle n of time integration (instant tn).
Suppose that
the old leapfrog-positions
,
for positions and velocities, respectively, at the cycle n of time integration (instant tn).
Suppose that
the old leapfrog-positions
![]() ,
reached from the instant tn to instant
tn-1/2,
is receding by a half time-step
,
reached from the instant tn to instant
tn-1/2,
is receding by a half time-step
![]() ,
where
,
where
![]() is a given time-step to advance positions
from time-level n-1/2 to n+1/2.
This time-step was estimated at time-level n-1/2,
obeying some stability condition
(e.g. Hilbert-Courant instability conditions).
is a given time-step to advance positions
from time-level n-1/2 to n+1/2.
This time-step was estimated at time-level n-1/2,
obeying some stability condition
(e.g. Hilbert-Courant instability conditions).
From the above considerations, we have the following second-order approximation for positions at time-level n from time-level n-1/2:
Second, consider the final leapfrog-positions,
![]() ,
obtained from the initial solution
,
obtained from the initial solution
![]() advancing from time-level n to n+1/2 by a half time-step,
advancing from time-level n to n+1/2 by a half time-step,
![]() ,
yielded at time-level n+1/2:
,
yielded at time-level n+1/2:
Thermal energies, or any other physical quantity obeying a first order differential equation of motion (e.g., magnetic field), may be advanced with an implicit
second order scheme.
Since specific thermal energy rate, ![]() ,
depends implicitly
on particle's position and velocity, (
,
depends implicitly
on particle's position and velocity, (
![]() ,
,
![]() ), it is quite convenient to synchronize thermal energies with positions.
Velocity terms in quantities like the
velocity-divergence, artificial viscosity etc.
shall be time-centered via Eq. (B7).
), it is quite convenient to synchronize thermal energies with positions.
Velocity terms in quantities like the
velocity-divergence, artificial viscosity etc.
shall be time-centered via Eq. (B7).
Considering the initial solutions
for the specific thermal energy and specific thermal energy rate to be
un-1/2 and
![]() respectively.
Time-centered solutions may be obtained by integrating from time-level n-1/2 to n, and receding the final solutions from time-level n+1/2 to n.
Both solutions can be written in a second order approximation:
respectively.
Time-centered solutions may be obtained by integrating from time-level n-1/2 to n, and receding the final solutions from time-level n+1/2 to n.
Both solutions can be written in a second order approximation:
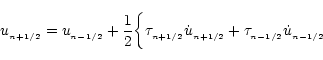
| (B12) |
Copyright The European Southern Observatory (ESO)