 |
(1) |
The present work adopts the traditional isotropically-adaptive SPH, where the smoothing length is proportional to the radius of a spherical region inside which there is a fixed number of nearest particles. However, more refined approaches of adaptive interpolation, regarding anisotropy of the mass distribution, may be seen in the literature (e.g., [Fulbright et al. 1995]; [Owen & Fisher 1994]; [Owen et al. 1998]; [Shapiro et al. 1996]).
We adopted the B-spline ([Monaghan & Gingold 1983]) to model the smoothing kernel, defined in 3-dimensions as:
We calculate the smoothed particle gradient of any fluid parameter A, for a particle i, by using the traditional form:
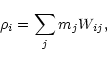 |
(3) |
The two-particle smoothing kernel, Wij, appearing in equations above is the symmetrized gather-scatter form, proposed by Hernquist & Katz (1989):
The usual form of writing the self-gravitating SPH momentum equation requires a symmetrized two-particle combination of pressure and artificial viscosity (see, e.g., Hernquist & Katz 1989; Monaghan 1992; Benz 1990):
The coefficient
![]() in Eq. (6) is usually
defined as the arithmetic mean of the adiabatic sound speed,
in Eq. (6) is usually
defined as the arithmetic mean of the adiabatic sound speed,
![]() ,
for particles i and j respectively.
However,
we found that the artificial viscosity works efficiently if we use the exact
definition of
,
for particles i and j respectively.
However,
we found that the artificial viscosity works efficiently if we use the exact
definition of ![]() in adiabatic shocks
but it
allows particle interpenetration if we adopt
the present molecular mixture and cooling,
mainly in the post-shocking layers where it has cooled down
to lower temperatures
as
in adiabatic shocks
but it
allows particle interpenetration if we adopt
the present molecular mixture and cooling,
mainly in the post-shocking layers where it has cooled down
to lower temperatures
as ![]() K.
The main reason for this effect is that a
considerable reduction in the specific
thermal energy occurs at lower temperatures,
which reduces considerably the local sound speed.
We minimized this effect replacing
K.
The main reason for this effect is that a
considerable reduction in the specific
thermal energy occurs at lower temperatures,
which reduces considerably the local sound speed.
We minimized this effect replacing
![]() by
the equivalent specific thermal energy of a (non-physical)
100% dissociated hydrogen cloud:
by
the equivalent specific thermal energy of a (non-physical)
100% dissociated hydrogen cloud:
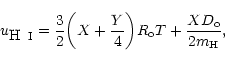 |
(8) |
Monaghan (1989) discussed an alternative solution to the problem of particle penetration in SPH. However, we have not adopted such device since the integration scheme has shown numerical instability on supersonic shocks in our calculations.
The interstellar clouds in our experiments are considered a mixture of atomic and molecular hydrogen, helium and traces of CO. Only H, H2 and He contribute effectively to the thermal energy; the role of CO is limited to the cooling of the gas, at temperatures lower than 104 K and at high densities. We assume that the chemical abundance (in mass) is X = 0.75 and Y = 0.25. The chemical equilibrium between H and H2 is the same of ML91, which is only valid in dark regions. The relative abundance, y, of atomic H obeys the equilibrium equation:
Temperatures are calculated by iterations from Eq. (11) predicting more accurate values by solving T from the linear term.
In general, convergence is reached within a good tolerance (
![]() )
after two or three iterations.
)
after two or three iterations.
The particle form of the first law of thermodynamics is expressed as
The cooling model takes into account two main processes that dominate in different ranges of temperature. Below 104 K the cooling is mostly due to molecules; we adopt the model of Hollenbach & McKee (1979, hereafter HM79). Above 104 K, free-free emission by electrons is the main cooling mechanism, which is well described by the DM72 cooling function. In the simulations presented in this work, the temperature reached values just above 104 K.
The total expression for the specific cooling rate in erg cm-3 s-1 is:
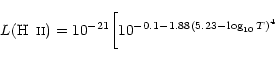
A plot of the cooling rate ![]() as
a function of the temperature,
for different number densities of hydrogen species, is shown in
Fig. 1.
The peak around 103 K is due to the cooling by H2, expressed by
the functions
as
a function of the temperature,
for different number densities of hydrogen species, is shown in
Fig. 1.
The peak around 103 K is due to the cooling by H2, expressed by
the functions
![]() and
and
![]() reported by HM79.
These functions rise strongly between 102 and 103 K, as
shown in Figs. 7 and 8 of HM79.
The steep decrease of the H2 contribution at about 103 K
is due to the dissociation of H2.
According to Eq. (9),
the relative abundance of molecular H,
is affected by a strong transition in
chemical equilibrium near 103 K.
This decrease does not appear in the figures
of HM79 because
they are interested in the cooling per H species and not
in the total effective cooling per cm3.
The CO contribution is evident in
Fig. 1 for high number
densities and T<104 K, since
its efficiency increases with
the square of the density of H species.
One can see in Fig. 1
that the cooling law is represented by
a straight line, for T<104 K and for
reported by HM79.
These functions rise strongly between 102 and 103 K, as
shown in Figs. 7 and 8 of HM79.
The steep decrease of the H2 contribution at about 103 K
is due to the dissociation of H2.
According to Eq. (9),
the relative abundance of molecular H,
is affected by a strong transition in
chemical equilibrium near 103 K.
This decrease does not appear in the figures
of HM79 because
they are interested in the cooling per H species and not
in the total effective cooling per cm3.
The CO contribution is evident in
Fig. 1 for high number
densities and T<104 K, since
its efficiency increases with
the square of the density of H species.
One can see in Fig. 1
that the cooling law is represented by
a straight line, for T<104 K and for
![]()
![]() ,
except for a small peak due to H2 cooling.
The H2-cooling profile is evident at low densities,
at temperatures lower than 104 K.
,
except for a small peak due to H2 cooling.
The H2-cooling profile is evident at low densities,
at temperatures lower than 104 K.
The heating mechanism is assumed to be a combination of the effect of cosmic rays and of H2 production by grains, according to the expressions given by Spitzer (1978). Heating by H2 formation on dust grains is effective below a critical temperature limit, of the order of 102 K, that depends on the surface texture of the grain. There are possibly many other heating processes in the interstellar medium. For instance, one possible mechanism we have not included here is the heating due to gas-grain collisions (e.g., [Spitzer 1978]; [Tielens & Hollenbach 1985]). We believe the mechanisms that we have taken into account are the dominant ones.
The heating by cosmic rays is given by
The present code belongs to a new class of hydrodynamic codes, called TreeSPH, which was originally developed by HK89. The main characteristic of TreeSPH is the computational reuse of the tree-descent on both gravity-calculations and neighbors-searching. Essentially, we followed the directions given by classical works in the literature (e.g., [Barnes 1990]; [Hernquist 1990]; HK89; [Makino 1990]) to construct the tree-subroutines.
One particular application of
the SPH-interpolation technique
is the program we
developed to visualize
the simulation results in gray scale or in pseudo-color images
(cf. Figs. 6 and 7).
To be visualized, each particle quantity
(e.g.,
density, temperature etc.)
is smeared out in a 2-D pixel-grid, and conveniently converted to pixel
quantities (8 or 24-bits).
As the out-put file of a given simulation
stores relevant SPH information (e.g., the smoothing
length h), the particle smoothing-length itself is used to cover
some pixels inside a radius
![]() ,
where
,
where ![]() (in length unit per pixel) is the grid scale-factor.
It may also be used to control the image
resolution.
The interpolation is performed with particles that obey some criterion (e.g.,
with densities or temperatures in a given range,
z-coordinate tolerance to define a slide
etc.).
(in length unit per pixel) is the grid scale-factor.
It may also be used to control the image
resolution.
The interpolation is performed with particles that obey some criterion (e.g.,
with densities or temperatures in a given range,
z-coordinate tolerance to define a slide
etc.).
A more complete version of the code, including a more complex cooling for the mixture H, H2, OH, H2O, CO, with the H, H2 and H2O chemistry shall be presented in a future paper.
Both gravity acceleration and potential field are calculated by means of the octal-tree scheme, called BH method (e.g., [Barnes & Hut 1986], 1989; [Hernquist 1987], 1988, 1990; [Makino 1990]), with the quadrupole approximation properly derived for the softened potential (see Appendix A).
Essentially, the same procedure to perform gravity calculations is applied to perform the nearest neighbors searching. The difference in both implementations, besides the specific calculations, is the stop-condition for tree-descents. On gravity computations, the stop condition is the essential of the BH method, which is described in several papers concerning this matter (e.g., Barnes & Hut 1986, 1989; Hernquist 1987, 1988).
In the nearest-neighbors searching (NNS), a tree-descent is performed in order to assemble for each particle a list of the nearest other particles that are separated with distances below or equal to a given radius R. The NNS tree-descent through a given cell stops if this one is unable to contain any neighbor inside, which may be translated to the following condition:
If the above condition is not satisfied, the focused cell may contain neighbors, and the tree-descent is resumed until the newly pointed cell encloses a single particle inside. This new candidate, with index j, is one of the nearest neighbors if the following condition is true:
| (25) |
The NNS algorithm itself is applied to determine the smoothing lengths.
The NNS routine returns,
for particle with index i,
a list of the nearest neighbors within an
input radius Ri.
If the number of neighbors found within Riexceeds an expected number
![]() ,
the list is sorted according to the neighbors distances, and then
the exceeding particles are discarded from the neighbors-list ([Heller 1993]).
Thus, the corrected radius is the maximum distance in the remaining neighbors-
list.
The smoothing length, in the case of the adopted kernel model
is then
,
the list is sorted according to the neighbors distances, and then
the exceeding particles are discarded from the neighbors-list ([Heller 1993]).
Thus, the corrected radius is the maximum distance in the remaining neighbors-
list.
The smoothing length, in the case of the adopted kernel model
is then
![]() .
.
If the number of neighbors found by the NNS procedure
is less than the expected
![]() ,
the new initial radius for neighbors search is twice the
old value so that a new cycle of search-and-sort is required
until a convergence criterion is satisfied.
It has been adopted adopted a tolerance of
,
the new initial radius for neighbors search is twice the
old value so that a new cycle of search-and-sort is required
until a convergence criterion is satisfied.
It has been adopted adopted a tolerance of ![]() neighbors in the present
work.
neighbors in the present
work.
For SPH computations, it is required a variant of the above algorithm to
assemble a list of the nearest particles that give non-zero contribution
to the smoothing kernel.
This effective-neighboring condition may enlarge the list for some
configurations, reaching increases of about
![]() .
We call this algorithm the effective-neighbors-search (ENS),
which consolidates the construction of the final neighbors list.
Along with an ENS tree-descent for a given particle i, any resolved
particle j is assigned as an effective neighbor if the relation
.
We call this algorithm the effective-neighbors-search (ENS),
which consolidates the construction of the final neighbors list.
Along with an ENS tree-descent for a given particle i, any resolved
particle j is assigned as an effective neighbor if the relation
![]() is satisfied.
is satisfied.
The adopted gravity softening is the classical Aarseth's approach,
where each particle is
is gravitationally equivalent to
a Plummer's sphere with the same mass of the original particle
and with a half-mass radius ![]() .
This approach does not reproduce Keplerian orbits even for a pair
of particles separated far beyond the effective-radius (
.
This approach does not reproduce Keplerian orbits even for a pair
of particles separated far beyond the effective-radius (
![]() ).
This problem is overcome by the softening scheme of
HK89, where the B-spline kernel itself is applied to perform the softening.
).
This problem is overcome by the softening scheme of
HK89, where the B-spline kernel itself is applied to perform the softening.
At the initialization of a new SPH (or pure-gravitational) experiment,
the program calculates iteratively
the maximum
softening length
![]() as a function of the gravity linear-scale:
as a function of the gravity linear-scale:
The energy ![]() depends on the chosen value for
depends on the chosen value for ![]() and the initial
value for
and the initial
value for ![]() ,
which can be zero or, if a pertinent
system's linear scale
lis known, its initial value can be
,
which can be zero or, if a pertinent
system's linear scale
lis known, its initial value can be
![]() in order to accelerate the
in order to accelerate the ![]() -determination.
Then, a new value for
-determination.
Then, a new value for ![]() is returned
from Eq. (26).
This corrected value for
is returned
from Eq. (26).
This corrected value for ![]() can be used
as a new initial value to repeat the above procedure,
allowing then
a more
accurate value for
can be used
as a new initial value to repeat the above procedure,
allowing then
a more
accurate value for ![]() .
In general, three iterations are sufficient
to reach a good value for
.
In general, three iterations are sufficient
to reach a good value for ![]() .
.
In order to perform calculations with spatially varying softening length,
we adopted the scatter form (HK89) since this allows quadrupole
approximation without involving spatial derivatives of ![]() .
However, we shall impose an upper limit
.
However, we shall impose an upper limit
![]() to the softening length, either being the one
calculated from Eq. (26),
at the initialization of the experiment, or an
input value,
so that the definitive softening length is written as
to the softening length, either being the one
calculated from Eq. (26),
at the initialization of the experiment, or an
input value,
so that the definitive softening length is written as
The multiple time-scale integration-scheme requires bookkeeping to control what particles are integrated with a given time-step, and how a time-step is selected regarding synchronization of the finite-differences solutions. One possible time scheme is the one illustrated in Fig. 2, where the finite-differences equations are solved along with a binary hierarchy of time-steps.
For each time-step, a list (time-bin)
of dynamically similar particles is assigned.
Each time-bin is indexed by a time-depth,
![]() ,
which, in turn, labels a time-step
,
which, in turn, labels a time-step
![]() ,
where
,
where
![]() is the root time-step that is calculated in the program
initializations.
For this reason, a time-step must be an ease-to-handle
floating-point, so that divisions by two will not compromise
the time integrity.
Thus, the chosen initial time-steps must be numbers like
0.0078125, 0.00390625 etc.
Numbers such as
is the root time-step that is calculated in the program
initializations.
For this reason, a time-step must be an ease-to-handle
floating-point, so that divisions by two will not compromise
the time integrity.
Thus, the chosen initial time-steps must be numbers like
0.0078125, 0.00390625 etc.
Numbers such as ![]() ,
,
![]() etc. will round-off on
divisions by two, inducing synchronization breaking,
and the program will hang due to infinite loops or it will at least incur
in wrong results.
etc. will round-off on
divisions by two, inducing synchronization breaking,
and the program will hang due to infinite loops or it will at least incur
in wrong results.
An upper-limit time-step is calculated from stability/accuracy considerations, which may be associated to the local physical properties. Regarding synchronization, the definitive time-step is determined as the maximum power of two that is smaller than or equal to the initial value.
For pure gravitational purposes the maximum time-step is adopted as being half of the cell's size divided by the particle's velocity (e.g., Jernigan & Porter 1989), assuming that the octal-tree itself is the standard of rest. For SPH simulations, the maximum individual time-step is calculated by the Courant stability condition:
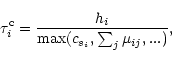 |
(28) |
| (29) |
The SPH equations of motion are integrated by means of a time-adaptive leapfrog,
so that corrections due to the changing of time-steps are explicitly included in
the finite-differences equations.
A particle may jump from a time-bin to another so that along its history the particle may have visited several time-bins.
The finite-differences scheme is derived in an approach similar of that given by
Hernquist & Katz (1989), so that positions and specific thermal energies are time-centered and velocities are synchronized with the time-level.
Thus, if the SPH particles are dynamically described by their position vector,
![]() ,
velocity,
,
velocity,
![]() ,
and specific thermal energy, un+1/2, we have the following finite difference equations:
,
and specific thermal energy, un+1/2, we have the following finite difference equations:
| (30) |
| (31) |
| (32) |
Time-centered velocities, appearing in the acceleration and in the specific thermal-energy-rate, are predicted by
| (33) |
Copyright The European Southern Observatory (ESO)