It is a common practice to test a new N-body code by integrating the
equations of motion of a simple system of particles known to be in a
steady state, and studying such things as relaxation effects and
conservation laws. Thus, we set up several N-body systems following
King's phase-space distribution function. We set the central density
parameter W0=5 in all cases. The units were chosen so that the total
mass M=1, the dispersion parameter
![]() ,
and the
gravitational constant G=1; with this set of units, the total energy
of the system is E=-1/2, and the global dynamical time
tD=1, so we are able to compare our results with those of
Hernquist & Barnes ([1990]) and Huang et al. ([1993]). Only
three runs are commented
here, namely those with N=4096, N=15000, and N=100 000.
,
and the
gravitational constant G=1; with this set of units, the total energy
of the system is E=-1/2, and the global dynamical time
tD=1, so we are able to compare our results with those of
Hernquist & Barnes ([1990]) and Huang et al. ([1993]). Only
three runs are commented
here, namely those with N=4096, N=15000, and N=100 000.
All the runs lasted 10 dynamical times. In particular, we ran the N=105 model over seven PCs, with the following processors: four Pentium/166 MHz, one Pentium Pro/200 MHz, one Pentium II/233 MHz and one Pentium II/266 MHz. To compute the CPU time demanded by the whole integration, we took the maximum among the CPU times of the processors in each cycle of integration, and summed up all these maxima to get the total. (If the program were perfectly balanced, all processors would finish simultaneously their respective tasks in each cycle; unfortunately, this could not be accomplished at all times, mainly due to the fact that our machines were not entirely dedicated to the integration. However, the performance was always near the ideal, since the program continually compensates the different third-party loads of the machines by redistributing adequately the number of particles assigned to each processor.) The integration of the ten dynamical times of the N=105 run consumed 9.5 hours of CPU; it involved 1000 time steps (100 time steps per dynamical time).
Table 1 compares the
speed of our code with that used by Hultman & Källander ([1997]).
In all these
experiments, only one processor was used. The fourth and fifth columns
give the CPU times when using a Pentium II-266 MHz processor running
a Linux operating system, and a HP 735 Workstation, respectively. The last
column shows the times reported by Hultman & Källander ([1997]),
whose code was also run
on a HP 735 Workstation. The (fixed) time steps in our simulations (third
column) were
equal to the shortest individual time steps of the experiments of
Hultman & Källander ([1997]). We can see that,
despite this last disadvantage, the
performance of our code increases with N, and with decreasing
![]() .
This is probably due to a better run over the tree when
computing accelerations.
.
This is probably due to a better run over the tree when
computing accelerations.
| N | PII 266 | HP 735 | HP 735 (H) | |||
| 4626 | 1.0 | 0.0039 | 1.0 | 1.9 | 1.9 | |
| 4626 | 0.1 | 0.0034 | 11.8 | 22.0 | 32.1 | |
| 15238 | 1.0 | 0.0063 | 2.7 | 5.0 | 9.4 |
![\begin{figure}\par\includegraphics[width=7cm]{ds1754f1.eps} \end{figure}](/articles/aas/full/2000/04/ds1754/Timg8.gif) |
Figure 1:
Standard deviation of relative particle energies |
In these preliminary simulations, all the standard tests were
satisfactory (e.g., energy was conserved better than 3 10-4 in
all cases). However, a test we found not to agree with previous results
(Hernquist & Barnes [1990]; Hultman & Källander [1997]).
This can be seen in Fig. 1, which shows the temporal behaviour of the
standard deviation
![]() of relative particle energies
of relative particle energies
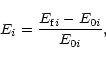 |
(1) |
Taking advantage of the speed of computation, we set up a pair of experiments in which two galaxies collide one another.
The first experiment was built with the aim of reproducing the
Antennæ (NGC 4038/4039), a classical model to simulate since the
pioneer work of Toomre & Toomre ([1972]).
We therefore needed a model for spiral
galaxies which remains stable at least during one dynamical time ![]() ,
i.e., a period which suffices to obtain only those features caused by the
collision, and not those caused by intrinsic evolution. To this end, we
first followed Hernquist's ([1993]) recipe for building compound galaxies.
However, this model proved not to be sufficiently stable
to our experiment: when isolated, it evolves significantly well before
the time at which the collision would begin. In most of our runs, a
,
i.e., a period which suffices to obtain only those features caused by the
collision, and not those caused by intrinsic evolution. To this end, we
first followed Hernquist's ([1993]) recipe for building compound galaxies.
However, this model proved not to be sufficiently stable
to our experiment: when isolated, it evolves significantly well before
the time at which the collision would begin. In most of our runs, a
![]() test of this model yields
test of this model yields
![]() at only
at only
![]() .
.
Therefore, we shifted to Barnes' ([1992]) model of compound
galaxy. We used an exponential disc with
![]() particles, mass
particles, mass
![]() ,
radial scale
,
radial scale
![]() ,
vertical scale z0=0.005, and
radial and vertical velocity dispersions in the ratio
,
vertical scale z0=0.005, and
radial and vertical velocity dispersions in the ratio
![]() .
For the bulge, we set up a King's sphere with
.
For the bulge, we set up a King's sphere with
![]() particles, central potential W0=3, total mass
particles, central potential W0=3, total mass
![]() ,
and the scale of velocities
,
and the scale of velocities ![]() .
Finally, for the
halo, we used a similar King's sphere but with
.
Finally, for the
halo, we used a similar King's sphere but with
![]() particles,
and total mass
particles,
and total mass
![]() .
Thus, the halo, disc and bulge masses are in the
relation 16:3:1, respectively, and their total mass is
.
Thus, the halo, disc and bulge masses are in the
relation 16:3:1, respectively, and their total mass is
![]() .
Fortunately, this compound galaxy proved to be stable at least during
.
Fortunately, this compound galaxy proved to be stable at least during
![]() .
.
Once obtained a satisfactory model for the galaxy, we set up the initial
conditions for the encounter leading to the Antennæ. We built a galaxy
with 20480 particles as before, replicated it, and put both copies on the
apocenter of a binary elliptical orbit with eccentricity e=0.5 and
pericentric distance
![]() ,
with the standard Antennæ inclinations for their angular momenta e.g., Barnes ([1988]). We set the
softening parameter
,
with the standard Antennæ inclinations for their angular momenta e.g., Barnes ([1988]). We set the
softening parameter
![]() ,
the tree aperture angle
,
the tree aperture angle
![]() ,
and a time step of
,
and a time step of
![]() .
Figure 2
shows the initial conditions (t=0) and the snapshot for
which the experiment best resembles the sky-view of NGC 4038/39
(
.
Figure 2
shows the initial conditions (t=0) and the snapshot for
which the experiment best resembles the sky-view of NGC 4038/39
(
![]() ). This simulation was run over six PCs (all the
abovementioned machines, except one of those with the Pentium 166 MHz
processor). The final time
). This simulation was run over six PCs (all the
abovementioned machines, except one of those with the Pentium 166 MHz
processor). The final time
![]() was achieved after 5.47 hours of
CPU time. In terms of speed of the code (Dubinsky [1996]),
i.e., the
number of particles which could be evaluated per second, this simulation
attained 2078 particles/s. (We disagree with the nomenclature here,
because this is not really a measure of the speed of the code itself,
but it depends on the number of processors involved. If we divide the
speed of the code by the number of processors, we get for our code 346
particles per second per processor; Dubinski's ([1996]) example,
as a comparison,
attains 375 particles per second per processor when using 16 processors.)
was achieved after 5.47 hours of
CPU time. In terms of speed of the code (Dubinsky [1996]),
i.e., the
number of particles which could be evaluated per second, this simulation
attained 2078 particles/s. (We disagree with the nomenclature here,
because this is not really a measure of the speed of the code itself,
but it depends on the number of processors involved. If we divide the
speed of the code by the number of processors, we get for our code 346
particles per second per processor; Dubinski's ([1996]) example,
as a comparison,
attains 375 particles per second per processor when using 16 processors.)
As a second simulation, we built up a King sphere with W0=12, total mass M=2, King radius r0=10-3, and N=512, and threw it against one of the above (initial) compound galaxies, with N=6144, in order to simulate the Cartwheel galaxy. The King's sphere was initially at 10 units away from the galaxy, i.e. at the outskirts of the halo. The relative velocity was V = 2 units, along the symmetry axis of the compound galaxy. Before choosing these parameters, a series of toy experiments with different masses, distances and velocities were run in order to achieve a good resemblance to the Cartwheel.
Figure 3 shows the final outcome of the simulation, from a point of view similar to that of the Earth. The experiment was run on one Pentium Pro/200 MHz and one Pentium II/266 MHz, and required 7.56 hours of CPU.
Copyright The European Southern Observatory (ESO)