From the tracks presented in this paper, we have constructed isochrones adopting the same algorithm of "equivalent evolutionary points'' as used in Bertelli et al. (1990, 1994).
The initial point of each isochrone is the 0.15 ![]() model in the
lower main sequence. The terminal stage of the isochrones is either
the tip of the TP-AGB for
model in the
lower main sequence. The terminal stage of the isochrones is either
the tip of the TP-AGB for
![]()
![]() (ages of
(ages of ![]() yr), or
C-ignition in the core for the remaining stars.
yr), or
C-ignition in the core for the remaining stars.
Theoretical luminosities and effective temperatures along the isochrones are translated to magnitudes and colors using extensive tabulations of bolometric corrections and colors, as in Bertelli et al. (1994). The tabulations were obtained from convolving the spectral energy distributions contained in the library of stellar spectra of Kurucz (1992) with the response function of several broad-band filters. The response functions are from Buser & Kurucz (1978) for the UBV pass-bands, from Bessell (1990) for the R and I Cousins, and finally from Bessell & Brett (1988) for the JHK ones.
In Fig. 5 we present some of the derived isochrones
on the HRD, sampled at age intervals of
![]() .
They cover the complete age range from about 0.06 to 16 Gyr.
Younger isochrones could be constructed only with the aid of
evolutionary tracks for stars with initial masses
.
They cover the complete age range from about 0.06 to 16 Gyr.
Younger isochrones could be constructed only with the aid of
evolutionary tracks for stars with initial masses
![]()
![]() ,
which
are not presented in this paper.
Complete tables with the isochrones can be obtained at the CDS in
Strasbourg, or upon request to the authors, or through the WWW site
http://pleiadi.pd.astro.it. In this data-base, isochrones are provided
at
,
which
are not presented in this paper.
Complete tables with the isochrones can be obtained at the CDS in
Strasbourg, or upon request to the authors, or through the WWW site
http://pleiadi.pd.astro.it. In this data-base, isochrones are provided
at
![]() intervals; this means that any two consecutive
isochrones differ by only 12 percent in their ages.
intervals; this means that any two consecutive
isochrones differ by only 12 percent in their ages.
For each isochrone table, the layout is as follows:
A header presents the basic information about the age and metallicity
of each isochrone. Column 1 presents the logarithm of the age in yr;
Cols. 2 and 3 the initial and actual stellar masses,
respectively. We recall that the initial mass is the useful quantity
for population synthesis calculations, since together with the initial
mass function it determines the relative number of stars in different
sections of the isochrones. Then follow the logarithms of surface
luminosity (Col. 4), effective temperature (Col. 5), and surface
gravity (Col. 6). From Cols. 7 to 15, we have the sequence of
absolute magnitudes, starting with the bolometric one and following
those in the UBVRIJHK pass-bands. In the last Col. (16), the
indefinite integral over the initial mass M of the initial mass
function (IMF) by number, i.e.
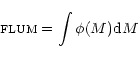 |
(1) |
|
|
|
|
|
|
MV | U-B | B-V | V-I | stage | |
| 7.80 | 5.6503 | 5.644 | 3.147 | 4.206 | 3.81 | -1.725 | -0.643 | -0.174 | -0.161 | TO |
| 7.80 | 6.3176 | 6.305 | 3.474 | 4.164 | 3.37 | -2.789 | -0.586 | -0.156 | -0.135 | Te-m |
| 7.80 | 6.3592 | 6.346 | 3.572 | 4.223 | 3.51 | -2.690 | -0.688 | -0.187 | -0.167 | Te-M |
| 7.80 | 6.3625 | 6.349 | 3.576 | 4.067 | 2.88 | -3.584 | -0.394 | -0.113 | -0.068 | L-M |
| 7.80 | 6.3666 | 6.353 | 3.314 | 3.656 | 1.50 | -3.026 | 1.170 | 1.222 | 1.155 | RGBb |
| 7.80 | 6.3733 | 6.356 | 3.898 | 3.588 | 0.64 | -3.845 | 1.806 | 1.542 | 1.657 | RGBt |
| 7.80 | 6.4397 | 6.397 | 3.491 | 3.635 | 1.24 | -3.291 | 1.458 | 1.348 | 1.282 | BHeb |
| 7.80 | 6.4899 | 6.440 | 3.686 | 3.819 | 1.78 | -4.523 | 0.230 | 0.363 | 0.431 | Te-M |
| 7.80 | 6.6046 | 6.530 | 3.703 | 3.612 | 0.94 | -3.599 | 1.697 | 1.473 | 1.438 | EHeb |
| 7.80 | 6.6152 | 6.526 | 4.317 | 3.553 | 0.09 | -4.262 | 1.813 | 1.581 | 2.230 | Cb |
| 9.00 | 1.7933 | 1.791 | 1.160 | 3.871 | 3.96 | 1.826 | 0.025 | 0.270 | 0.308 | TO |
| 9.00 | 2.0510 | 2.047 | 1.443 | 3.825 | 3.55 | 1.148 | 0.004 | 0.414 | 0.495 | Te-m |
| 9.00 | 2.0663 | 2.062 | 1.609 | 3.890 | 3.65 | 0.693 | 0.107 | 0.181 | 0.205 | Te-M |
| 9.00 | 2.0671 | 2.063 | 1.560 | 3.827 | 3.45 | 0.851 | 0.014 | 0.406 | 0.486 | L-M |
| 9.00 | 2.0728 | 2.068 | 1.292 | 3.713 | 3.26 | 1.747 | 0.494 | 0.883 | 0.906 | RGBb |
| 9.00 | 2.0866 | 2.080 | 2.353 | 3.635 | 1.89 | -0.454 | 1.293 | 1.283 | 1.280 | RGBt |
| 9.00 | 2.0913 | 2.084 | 1.528 | 3.691 | 2.94 | 1.253 | 0.683 | 0.991 | 0.996 | BHeb |
| 9.00 | 2.1686 | 2.159 | 1.620 | 3.692 | 2.87 | 1.016 | 0.677 | 0.987 | 0.989 | Te-M |
| 9.00 | 2.2986 | 2.283 | 2.113 | 3.664 | 2.28 | -0.056 | 0.978 | 1.135 | 1.124 | EHeb |
| 9.00 | 2.3080 | 2.279 | 3.326 | 3.564 | 0.67 | -2.051 | 1.818 | 1.570 | 2.000 | 1TP |
| 9.00 | 2.3096 | 0.672 | 4.069 | 3.473 | -0.97 | -1.287 | 1.377 | 1.617 | 3.764 | AGBt |
| 10.20 | 0.8938 | 0.892 | 0.090 | 3.742 | 4.21 | 4.665 | 0.269 | 0.748 | 0.791 | TO |
| 10.20 | 0.9190 | 0.917 | 0.240 | 3.702 | 3.91 | 4.436 | 0.557 | 0.917 | 0.955 | RGBb |
| 10.20 | 0.9321 | 0.927 | 1.350 | 3.653 | 2.61 | 1.928 | 1.021 | 1.162 | 1.184 | L-M |
| 10.20 | 0.9324 | 0.926 | 1.289 | 3.656 | 2.69 | 2.057 | 0.984 | 1.143 | 1.167 | L-m |
| 10.20 | 0.9342 | 0.743 | 3.370 | 3.485 | -0.18 | 0.191 | 1.399 | 1.615 | 3.577 | RGBt |
| 10.20 | 0.9342 | 0.743 | 1.574 | 3.666 | 2.35 | 1.276 | 0.948 | 1.121 | 1.112 | BHeb |
| 10.20 | 0.9343 | 0.742 | 1.625 | 3.661 | 2.27 | 1.180 | 0.999 | 1.146 | 1.135 | Te-m |
| 10.20 | 0.9354 | 0.738 | 1.586 | 3.670 | 2.35 | 1.220 | 0.916 | 1.104 | 1.093 | Te-M |
| 10.20 | 0.9363 | 0.735 | 2.019 | 3.631 | 1.76 | 0.415 | 1.360 | 1.311 | 1.303 | EHeb |
| 10.20 | 0.9363 | 0.734 | 2.267 | 3.609 | 1.42 | 0.017 | 1.647 | 1.450 | 1.454 | L-M |
| 10.20 | 0.9363 | 0.733 | 2.142 | 3.620 | 1.59 | 0.210 | 1.502 | 1.377 | 1.373 | L-m |
| 10.20 | 0.9365 | 0.674 | 3.314 | 3.487 | -0.15 | 0.275 | 1.404 | 1.614 | 3.537 | 1TP |
| 10.20 | 0.9365 | 0.529 | 3.499 | 3.465 | -0.53 | 0.315 | 1.362 | 1.618 | 3.886 | AGBt |
We also provide summary tables containing
basic information for the most significant stages along the
isochrones. A sample table of this kind is presented in
Table 3 below, for three Z=0.019 isochrones, with age
values
![]() ,
9.0 and 10.2.
The evolutionary stages are listed in the last column, and are,
in sequence:
,
9.0 and 10.2.
The evolutionary stages are listed in the last column, and are,
in sequence:
TO: the turn-off point, i.e.
the point of highest
Te-m and Te-M signal
the coldest and hottest points, respectively, of stars in the
overall contraction phase at the end of core-H burning;
in this case Te-M roughly corresponds to the stars in the
stage of core H-exhaustion. Occasionally, this stage is followed by
a local maximum of luminosity, L-M, of stars which are crossing
Hertzsprung gap;
RGBb: the base of the RGB;
L-M and L-m limit
the luminosity interval of RGB stars which are crossing the
discontinuity in chemical profile left by the first dredge-up
event; so, this interval corresponds to the bump in the
luminosity function along the RGB;
RGBt: the tip of the RGB;
BHeb: the beginning of the CHeB phase. It is
defined as the point of lowest luminosity for CHeB stars;
Te-m and Te-M signal
the coldest and hottest points, respectively, for CHeB stars.
For the youngest isochrones, Te-M represents the maximum
extension of the Cepheid loop;
EHeb: the end of the CHeB phase;
L-M and L-m
limit the luminosity range of early-AGB stars; this interval
corresponds to the clump of early-AGB stars in colour-magnitude
diagrams;
1TP: the beginning of the thermally pulsing
AGB phase;
AGBt: the end of the AGB phase;
Cb: the stage of C-ignition in the cases the
AGB phase does not occur.
In addition, we provide tables with the integrated broad-band colours of single-burst stellar populations. Such tables are derived by integrating the stellar luminosities, weighted by the predicted number of stars in each bin, along the isochrones.
Copyright The European Southern Observatory (ESO)